1.3 — Perfect Competition I
ECON 326 • Industrial Organization • Spring 2023
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/ioS23
ioS23.classes.ryansafner.com
Recall: The Firm's Two Problems
1st Stage: firm's profit maximization problem:
Choose: < output >
In order to maximize: < profits >
2nd Stage: firm's cost minimization problem:
Choose: < inputs >
In order to minimize: < cost >
Subject to: < producing the optimal output >
- Minimizing costs ⟺ maximizing profits

Visualizing Total Profit As R(q)−C(q)
- π(q)=R(q)−C(q)
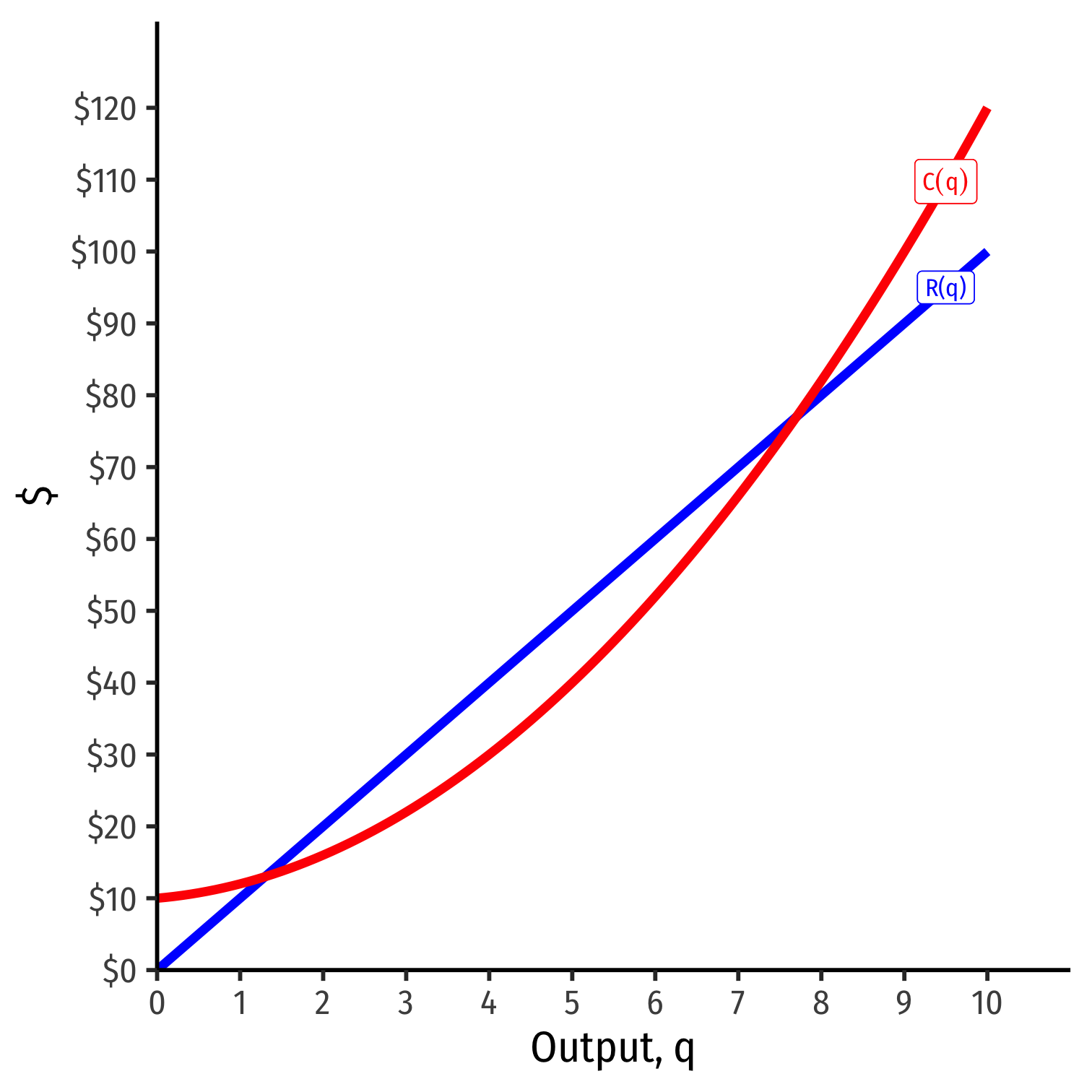
Visualizing Total Profit As R(q)−C(q)
- π(q)=R(q)−C(q)

Visualizing Total Profit As R(q)−C(q)
π(q)=R(q)−C(q)
Graph: find q∗ to max π⟹q∗ where max distance between R(q) and C(q)

Visualizing Total Profit As R(q)−C(q)
π(q)=R(q)−C(q)
Graph: find q∗ to max π⟹q∗ where max distance between R(q) and C(q)
Slopes must be equal: MR(q)=MC(q)
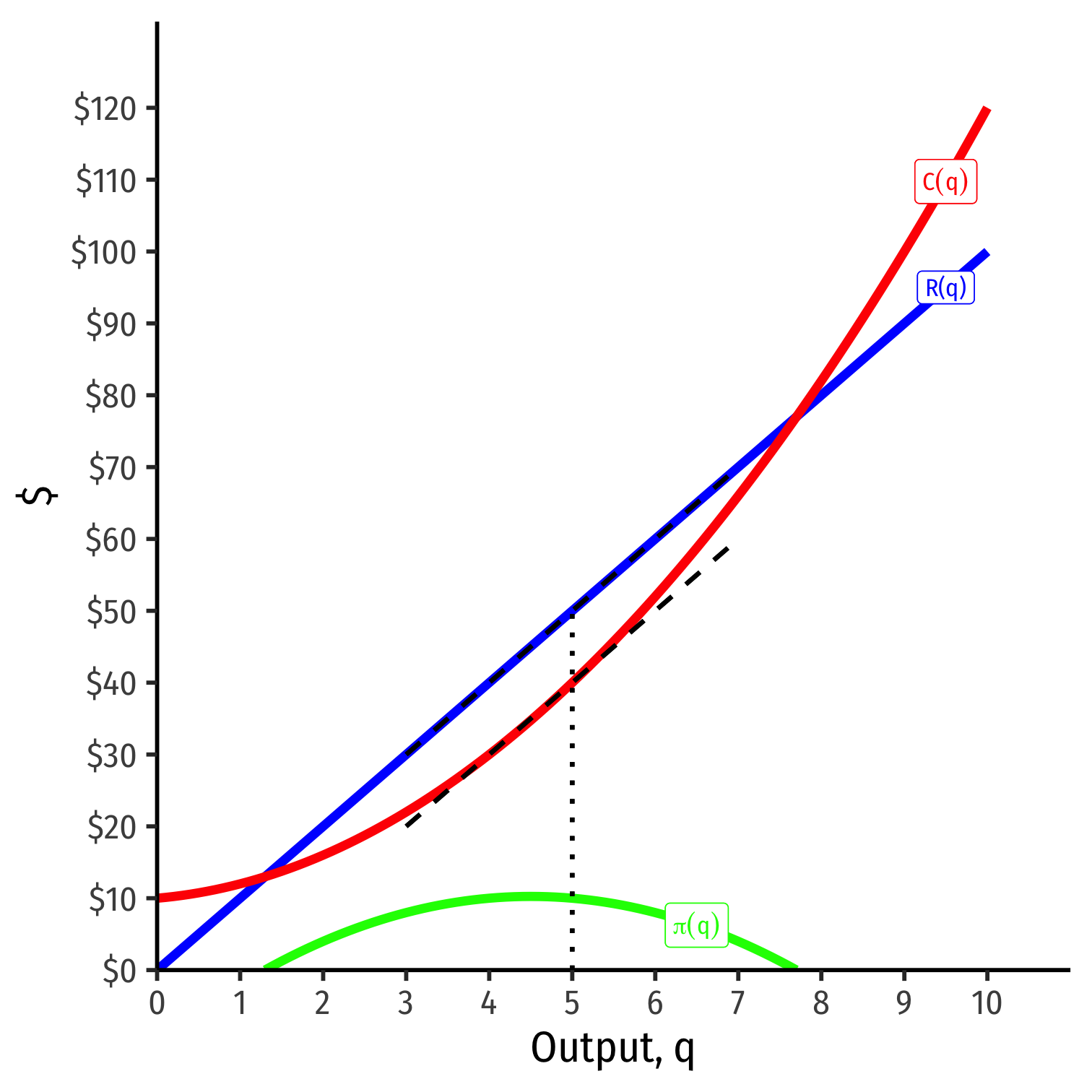
Visualizing Total Profit As R(q)−C(q)
π(q)=R(q)−C(q)
Graph: find q∗ to max π⟹q∗ where max distance between R(q) and C(q)
Slopes must be equal: MR(q)=MC(q)
- At q∗=5:
- R(q)=50
- C(q)=40
- π(q)=10
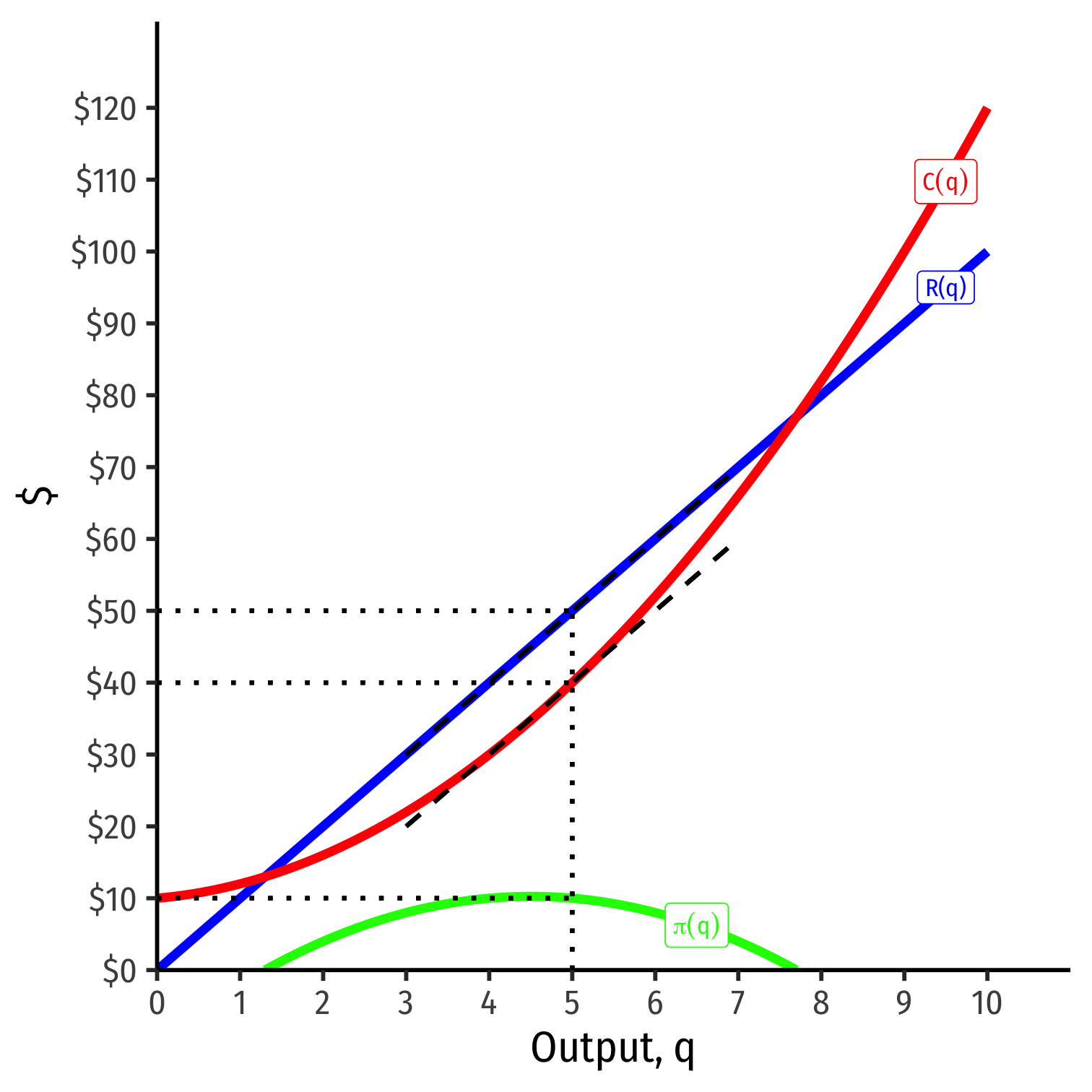
Visualizing Profit Per Unit As MR(q) and MC(q)
- At low output q<q∗, can increase π by producing more: MR(q)>MC(q)

Visualizing Profit Per Unit As MR(q) and MC(q)
- At high output q>q∗, can increase π by producing less: MR(q)<MC(q)
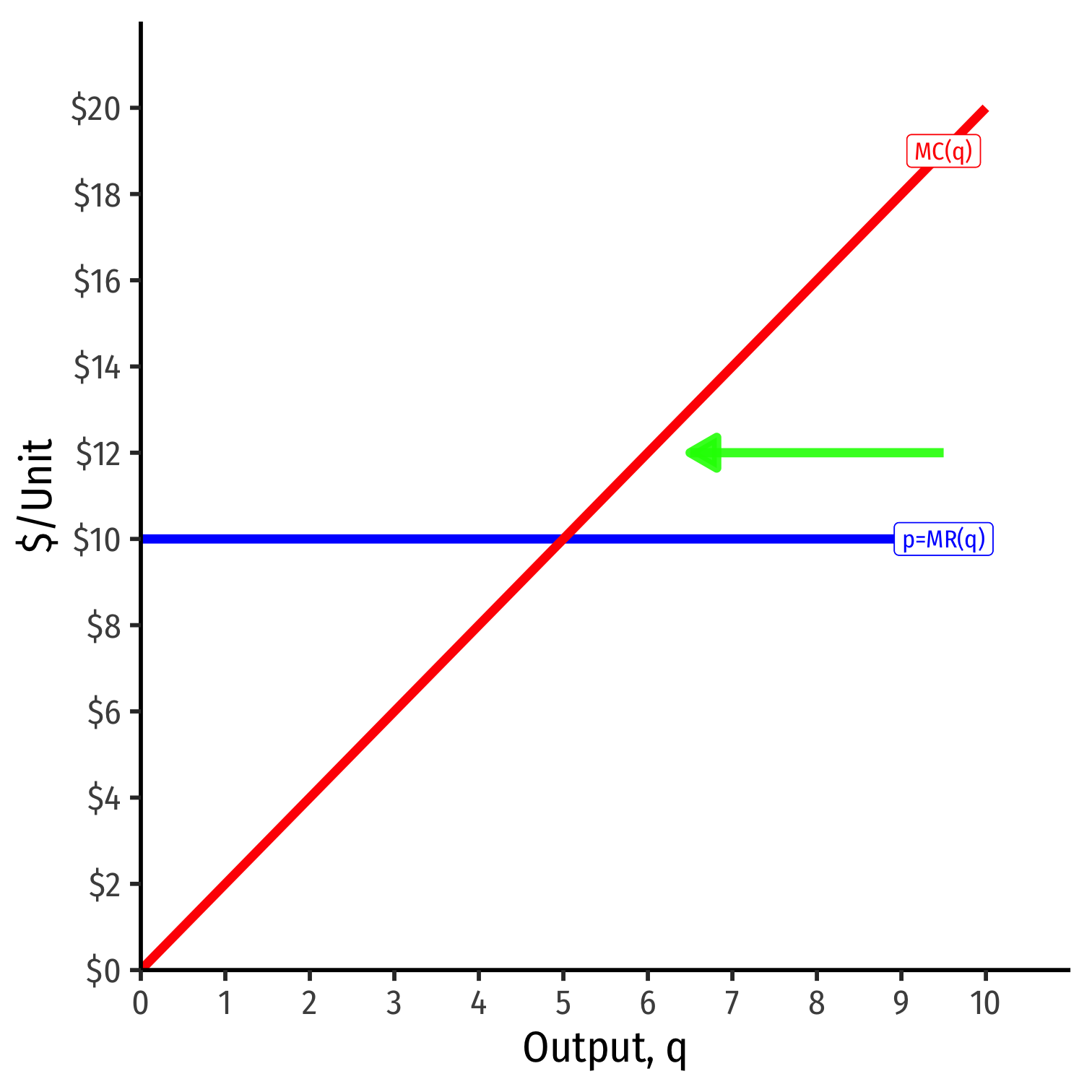
Visualizing Profit Per Unit As MR(q) and MC(q)
- π is maximized where MR(q)=MC(q)
Comparative Statics
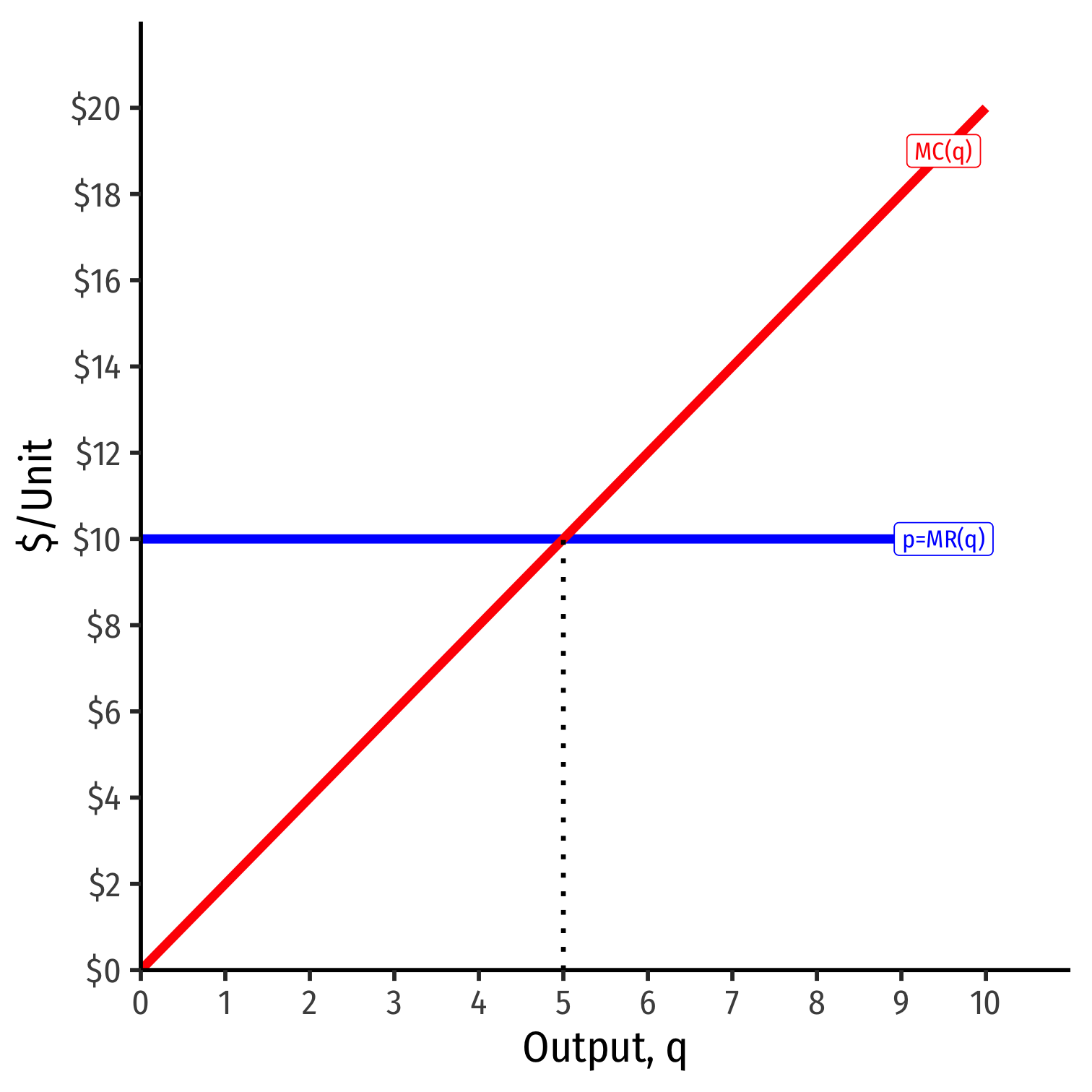
If Market Price Changes I
Suppose the market price increases
Firm (always setting MR=MC) will respond by producing more
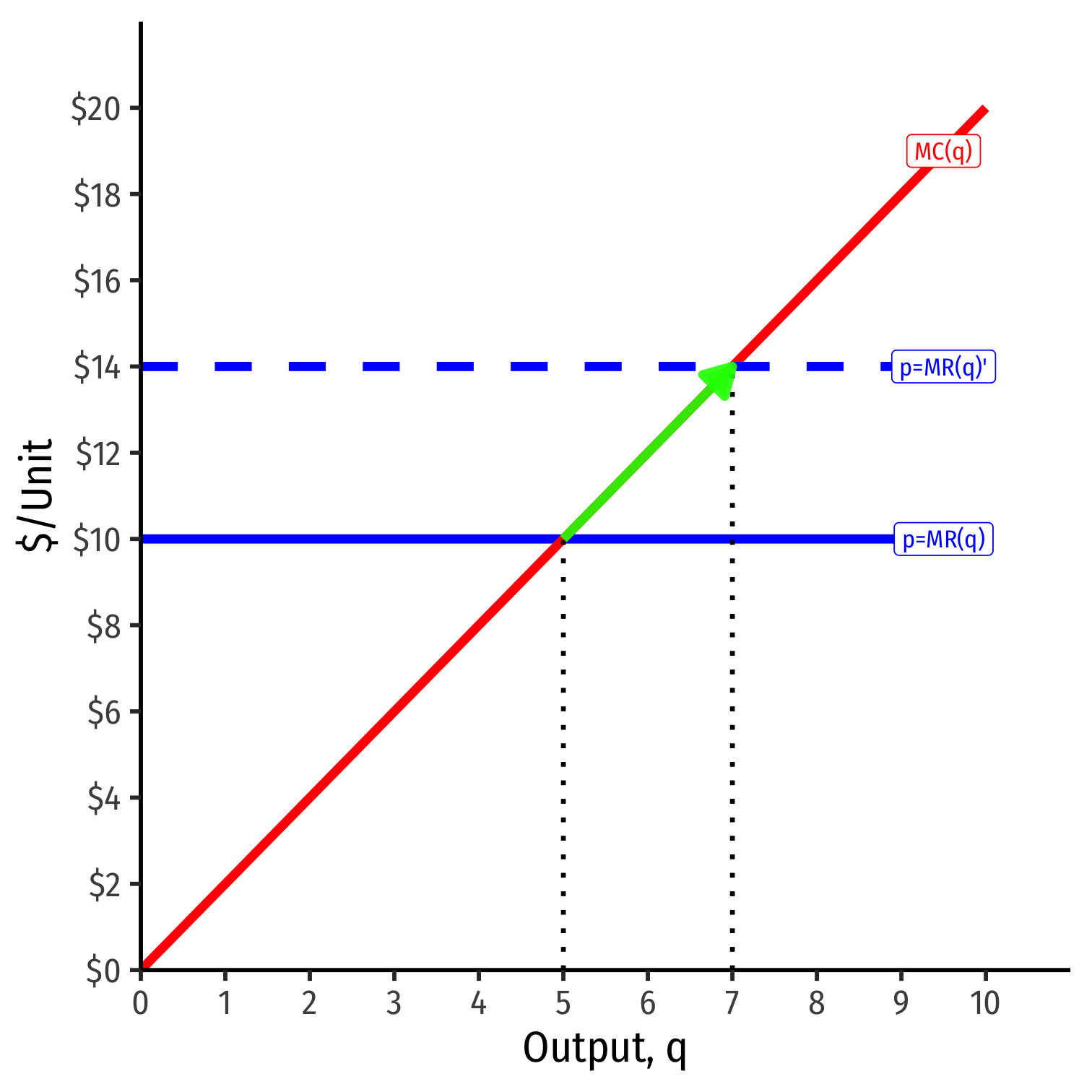
If Market Price Changes II
Suppose the market price decreases
Firm (always setting MR=MC) will respond by producing less

The Firm’s Supply Curve
- The firm’s marginal cost curve is its supply curve‡
p=MC(q)
- How it will supply the optimal amount of output in response to the market price
- Firm always sets its price equal to its marginal cost
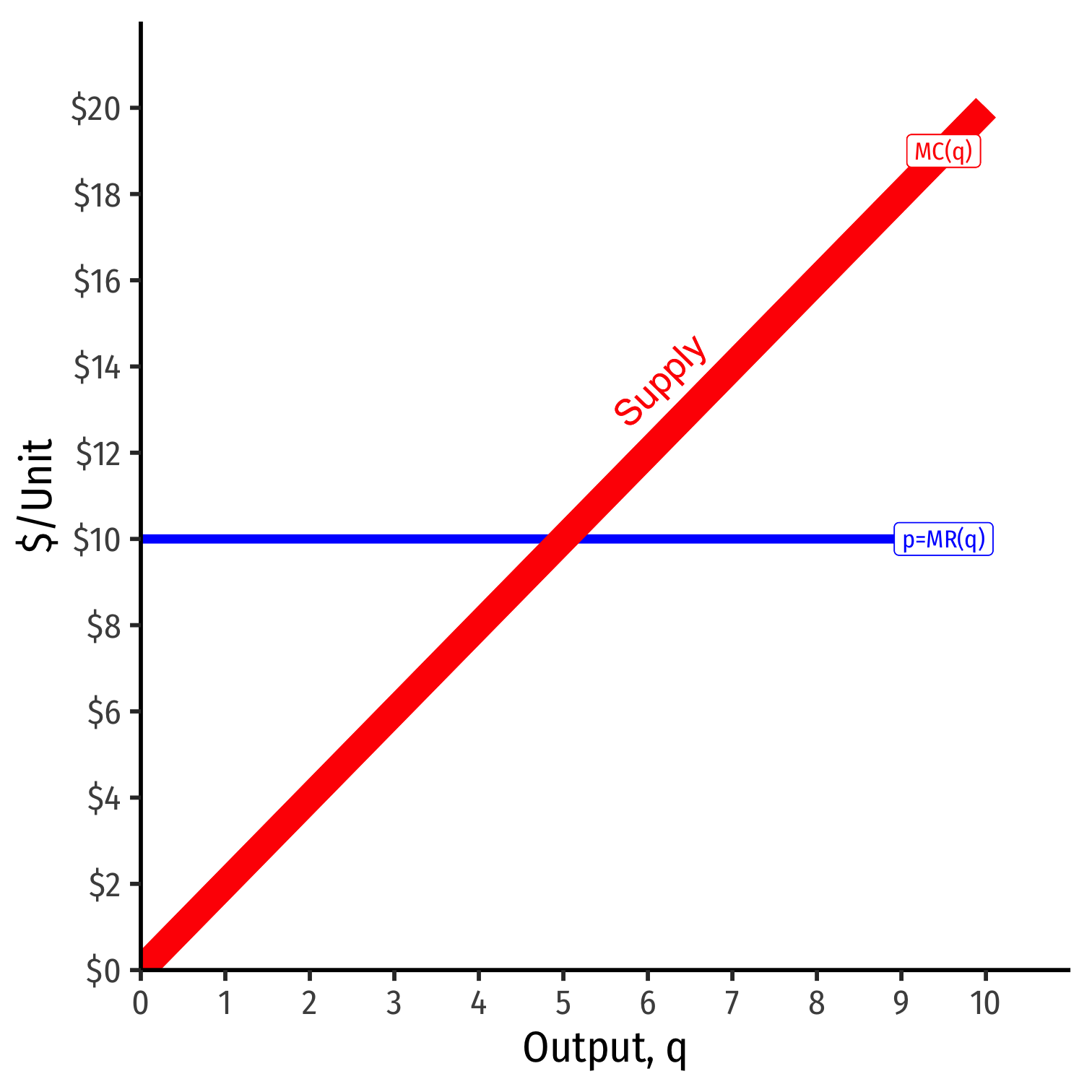
‡ Mostly...there is an important exception we will see shortly!
Calculating Profit
Calculating (Average) Profit as AR(q)-AC(q)
- Profit is π(q)=R(q)−C(q)

Calculating (Average) Profit as AR(q)-AC(q)
Profit is π(q)=R(q)−C(q)
Profit per unit can be calculated as: π(q)q=AR(q)−AC(q)=p−AC(q)

Calculating (Average) Profit as AR(q)-AC(q)
Profit is π(q)=R(q)−C(q)
Profit per unit can be calculated as: π(q)q=AR(q)−AC(q)=p−AC(q)
Multiply by q to get total profit: π(q)=q[p−AC(q)]
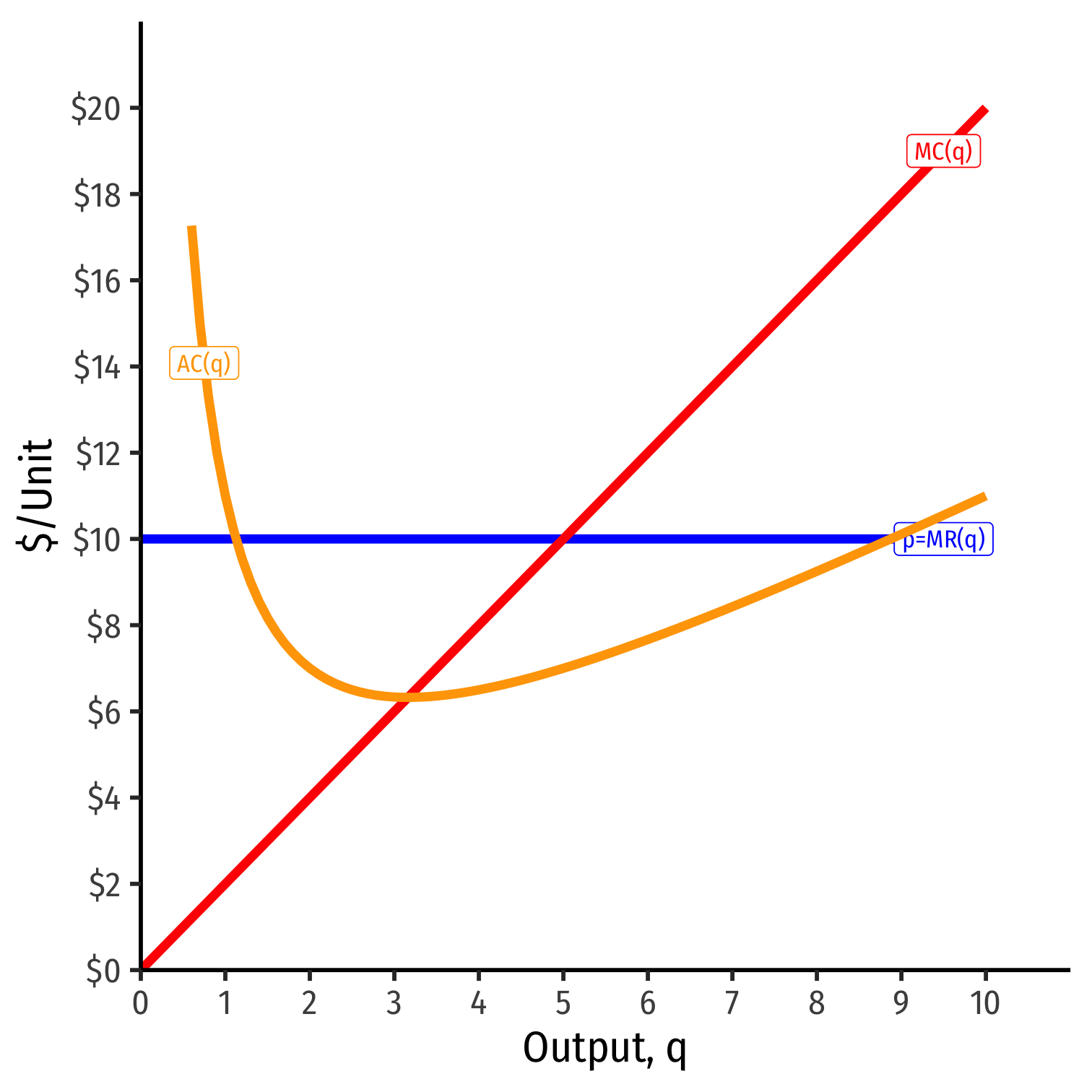
Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $10
At q* = 5 (per unit):
At q* = 5 (totals):

Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $10
At q* = 5 (per unit):
- AR(5) = $10/unit
At q* = 5 (totals):
- R(5) = $50

Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $10
At q* = 5 (per unit):
- AR(5) = $10/unit
- AC(5) = $7/unit
At q* = 5 (totals):
- R(5) = $50
- C(5) = $35
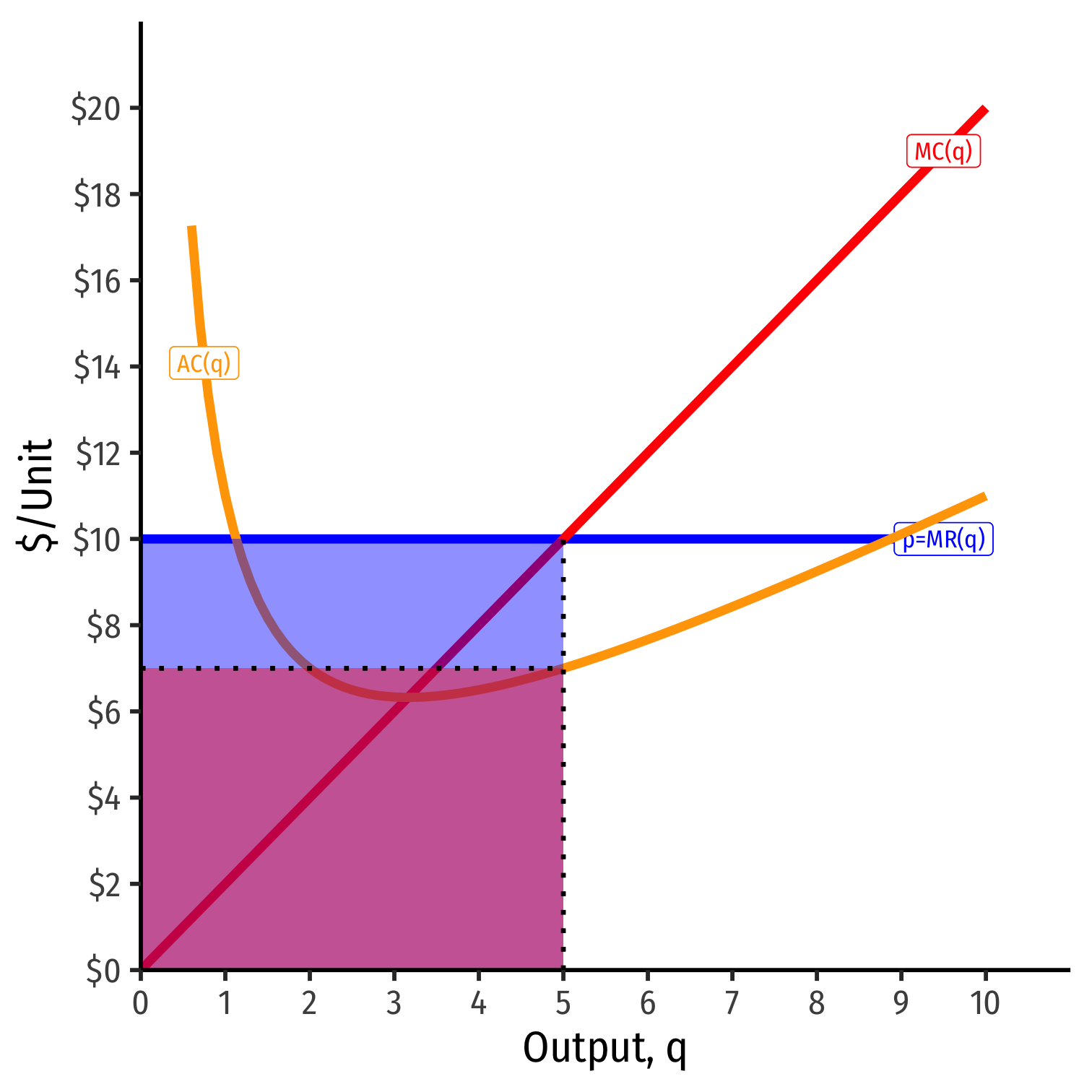
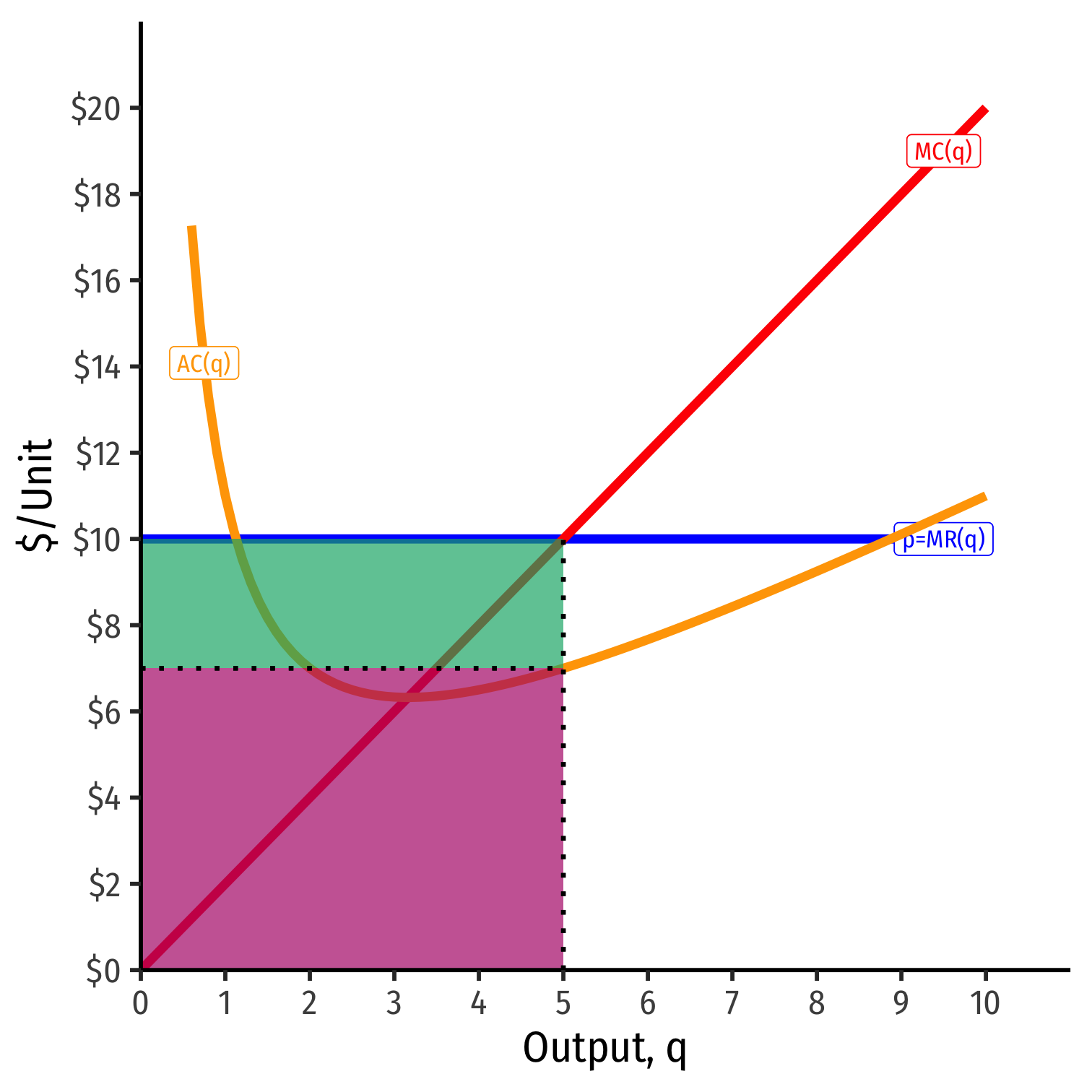
Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $10
At q* = 5 (per unit):
- AR(5) = $10/unit
- AC(5) = $7/unit
- Aπ(5) = $3/unit
At q* = 5 (totals):
- R(5) = $50
- C(5) = $35
- π = $15
Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $2
At q* = 1 (per unit):
At q* = 1 (totals):
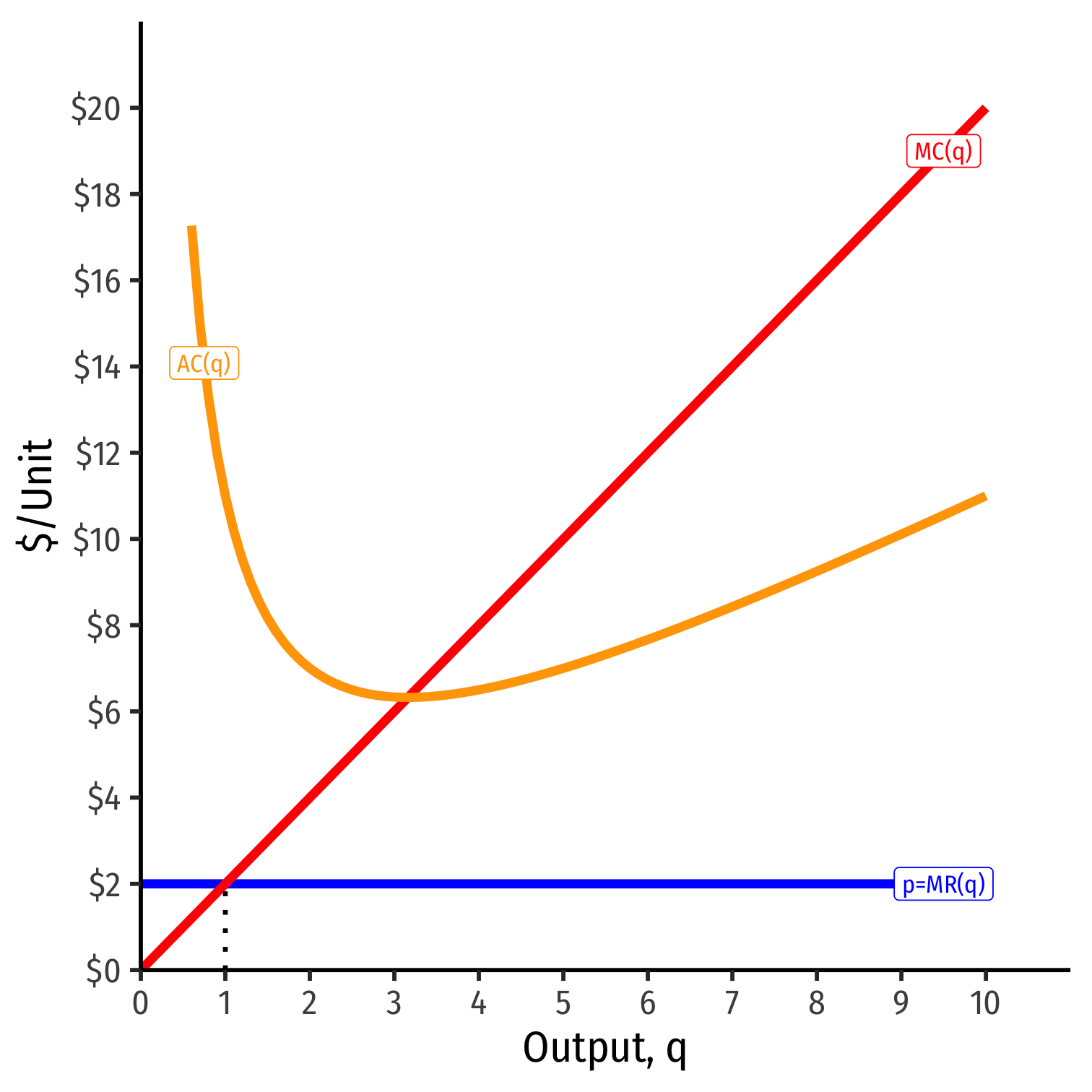
Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $2
At q* = 1 (per unit):
- AR(1) = $2/unit
At q* = 1 (totals):
- R(1) = $2

Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $2
At q* = 1 (per unit):
- AR(1) = $2/unit
- AC(1) = $10/unit
At q* = 1 (totals):
- R(1) = $2
- C(1) = $10

Calculating (Average) Profit as AR(q)-AC(q)
At market price of p* = $2
At q* = 1 (per unit):
- AR(1) = $2/unit
- AC(1) = $10/unit
- Aπ(1) = -$8/unit
At q* = 1 (totals):
- R(1) = $2
- C(1) = $10
- π(1) = -$8

Short-Run Shut-Down Decisions
Short-Run Shut-Down Decisions
What if a firm's profits at q∗ are negative (i.e. it earns losses)?
Should it produce at all?

Short-Run Shut-Down Decisions
Suppose firm chooses to produce nothing (q=0):
If it has fixed costs (f>0), its profits are:
π(q)=pq−C(q)

Short-Run Shut-Down Decisions
Suppose firm chooses to produce nothing (q=0):
If it has fixed costs (f>0), its profits are:
π(q)=pq−C(q)π(q)=pq−f−VC(q)

Short-Run Shut-Down Decisions
Suppose firm chooses to produce nothing (q=0):
If it has fixed costs (f>0), its profits are:
π(q)=pq−C(q)π(q)=pq−f−VC(q)π(0)=−f
i.e. it (still) pays its fixed costs

Short-Run Shut-Down Decisions
- A firm should choose to produce no output (q=0) only when:
π from producing<π from not producing
Short-Run Shut-Down Decisions
- A firm should choose to produce no output (q=0) only when:
π from producing<π from not producingπ(q)<−f
Short-Run Shut-Down Decisions
- A firm should choose to produce no output (q=0) only when:
π from producing<π from not producingπ(q)<−fpq−VC(q)−f<−f
Short-Run Shut-Down Decisions
- A firm should choose to produce no output (q=0) only when:
π from producing<π from not producingπ(q)<−fpq−VC(q)−f<−fpq−VC(q)<0
Short-Run Shut-Down Decisions
- A firm should choose to produce no output (q=0) only when:
π from producing<π from not producingπ(q)<−fpq−VC(q)−f<−fpq−VC(q)<0pq<VC(q)
Short-Run Shut-Down Decisions
- A firm should choose to produce no output (q=0) only when:
π from producing<π from not producingπ(q)<−fpq−VC(q)−f<−fpq−VC(q)<0pq<VC(q)p<AVC(q)
- Shut down price: firm will shut down production in the short run when p<AVC(q)

The Firm’s Short Run Supply Decision
The Firm’s Short Run Supply Decision
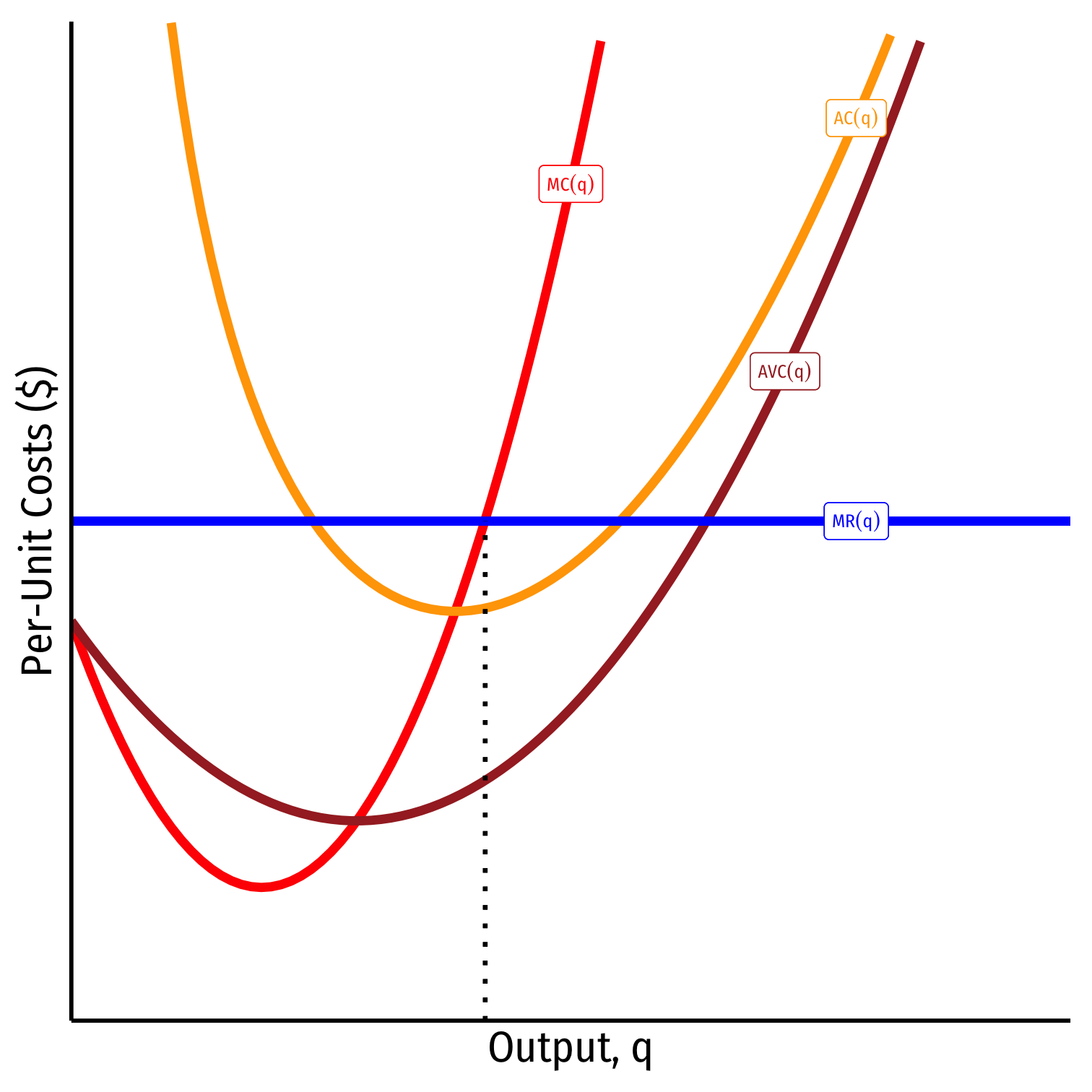
The Firm's Short Run Supply Decision

The Firm's Short Run Supply Decision
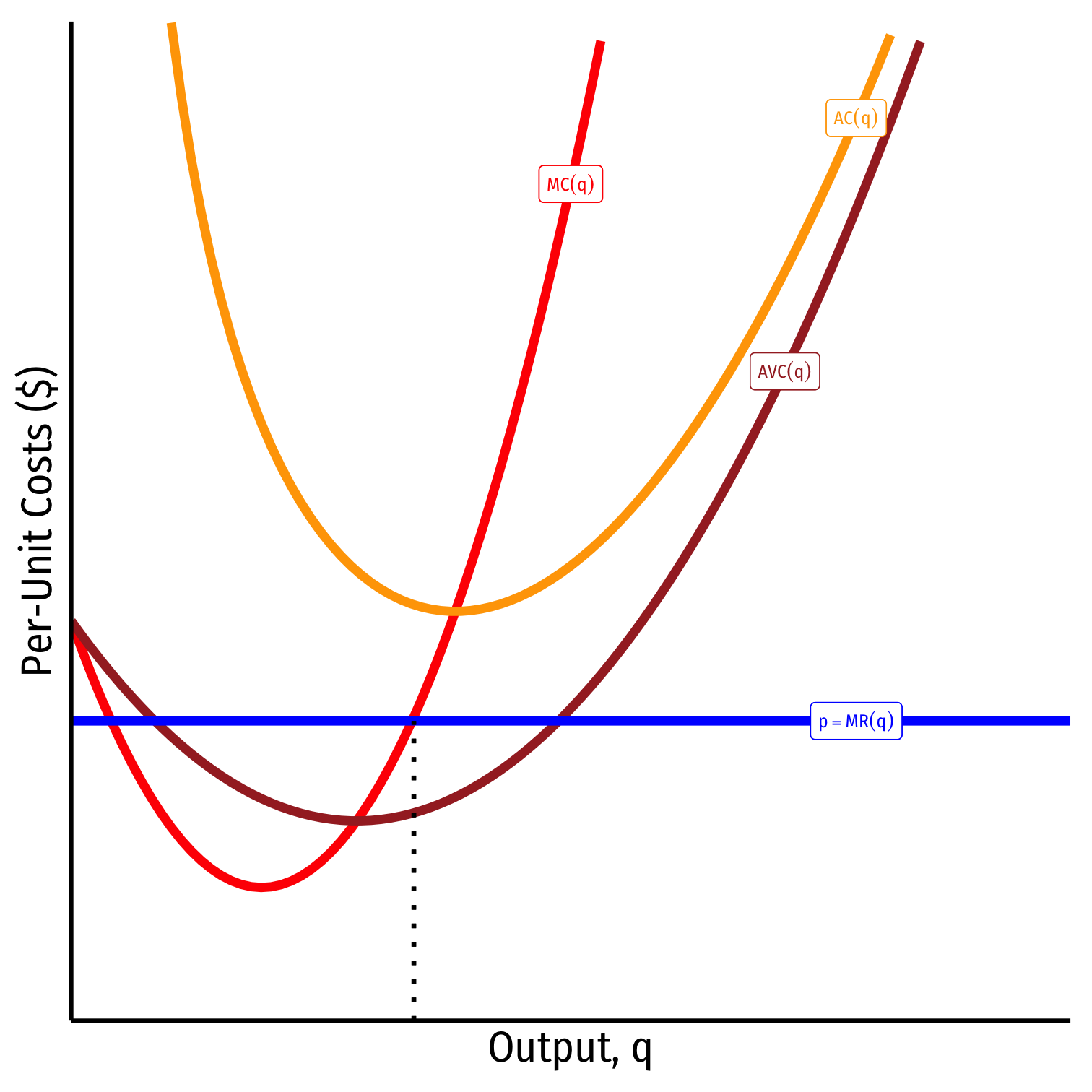
The Firm's Short Run Supply Decision

The Firm's Short Run Supply Decision
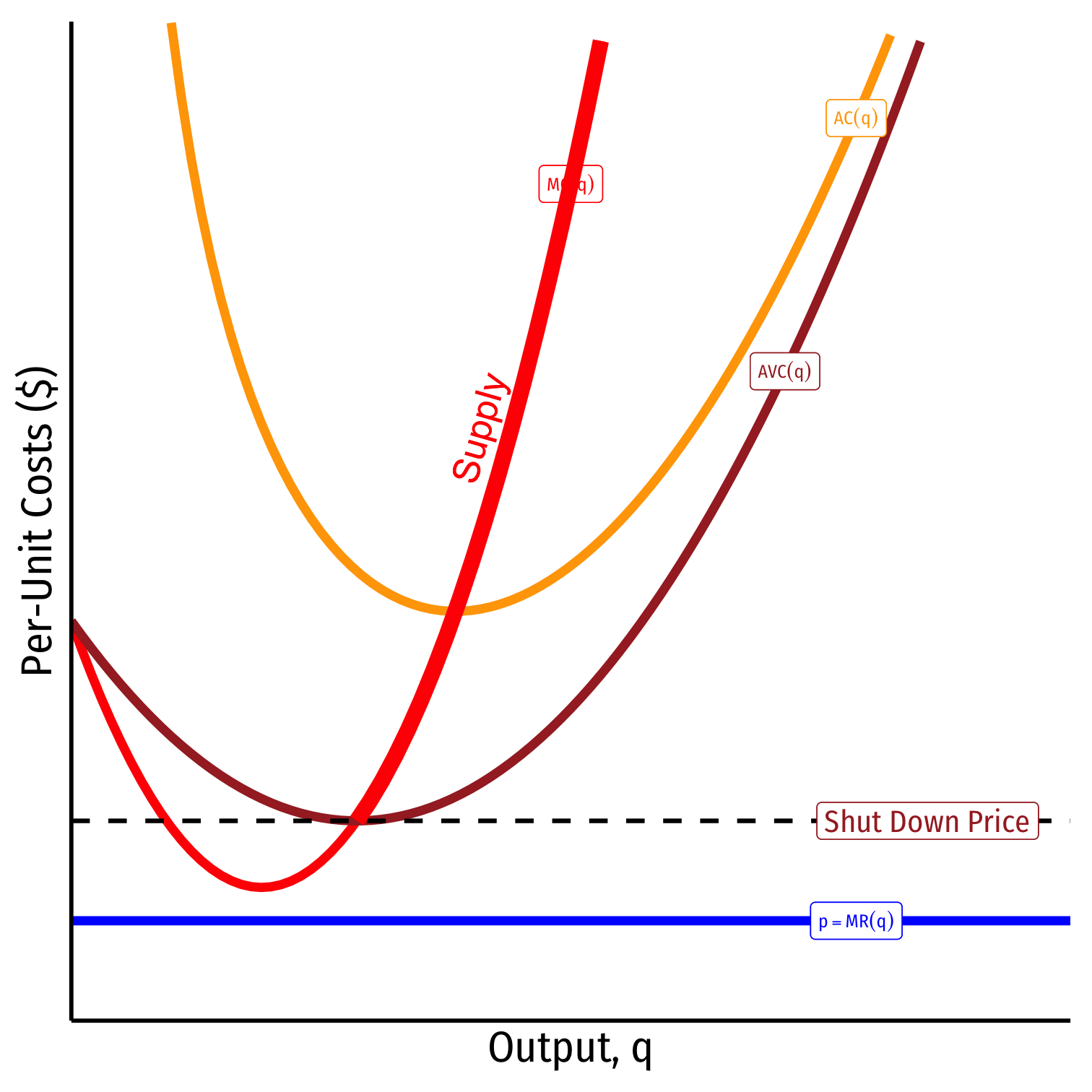
The Firm's Short Run Supply Decision
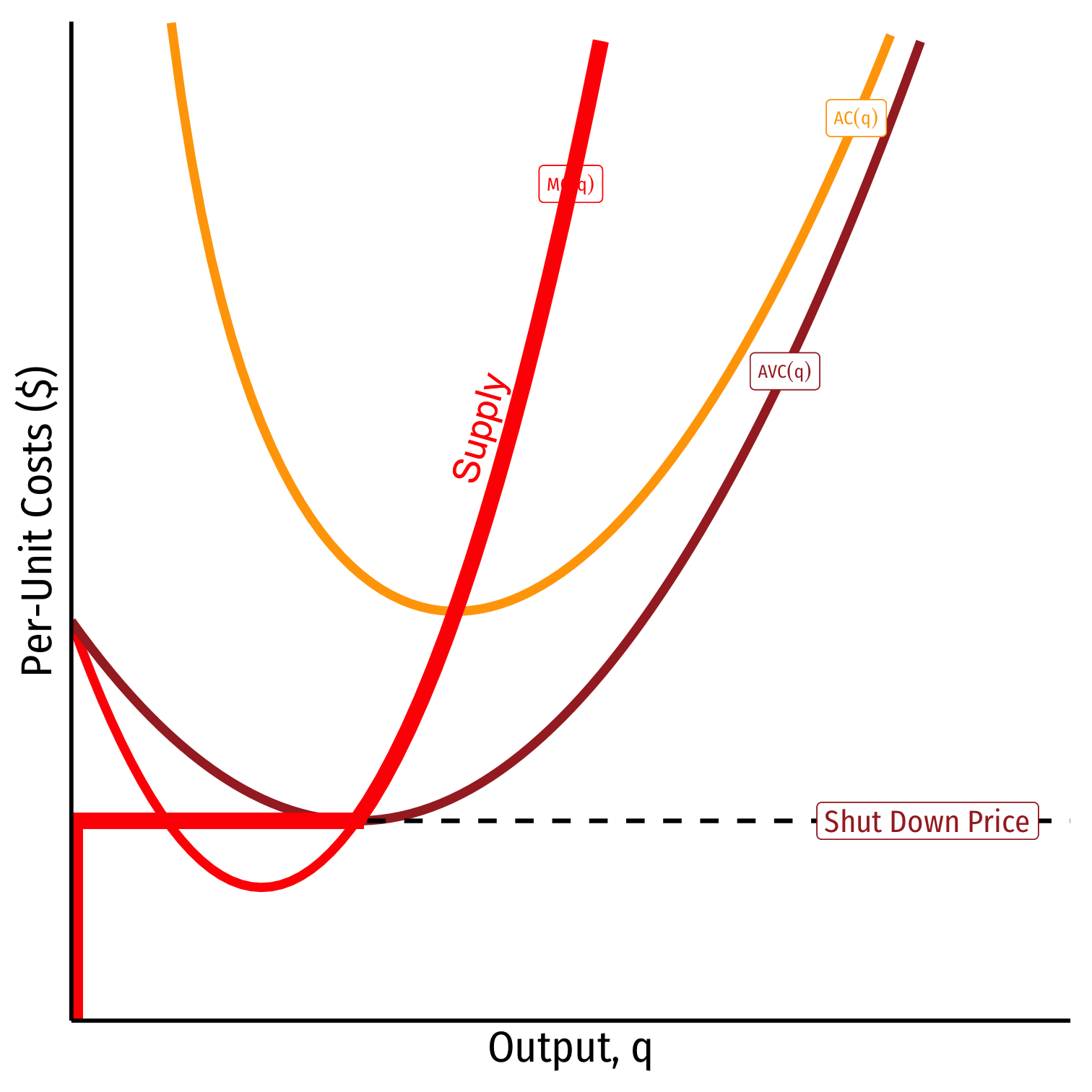
Firm’s short run supply curve:
The Firm's Short Run Supply Decision
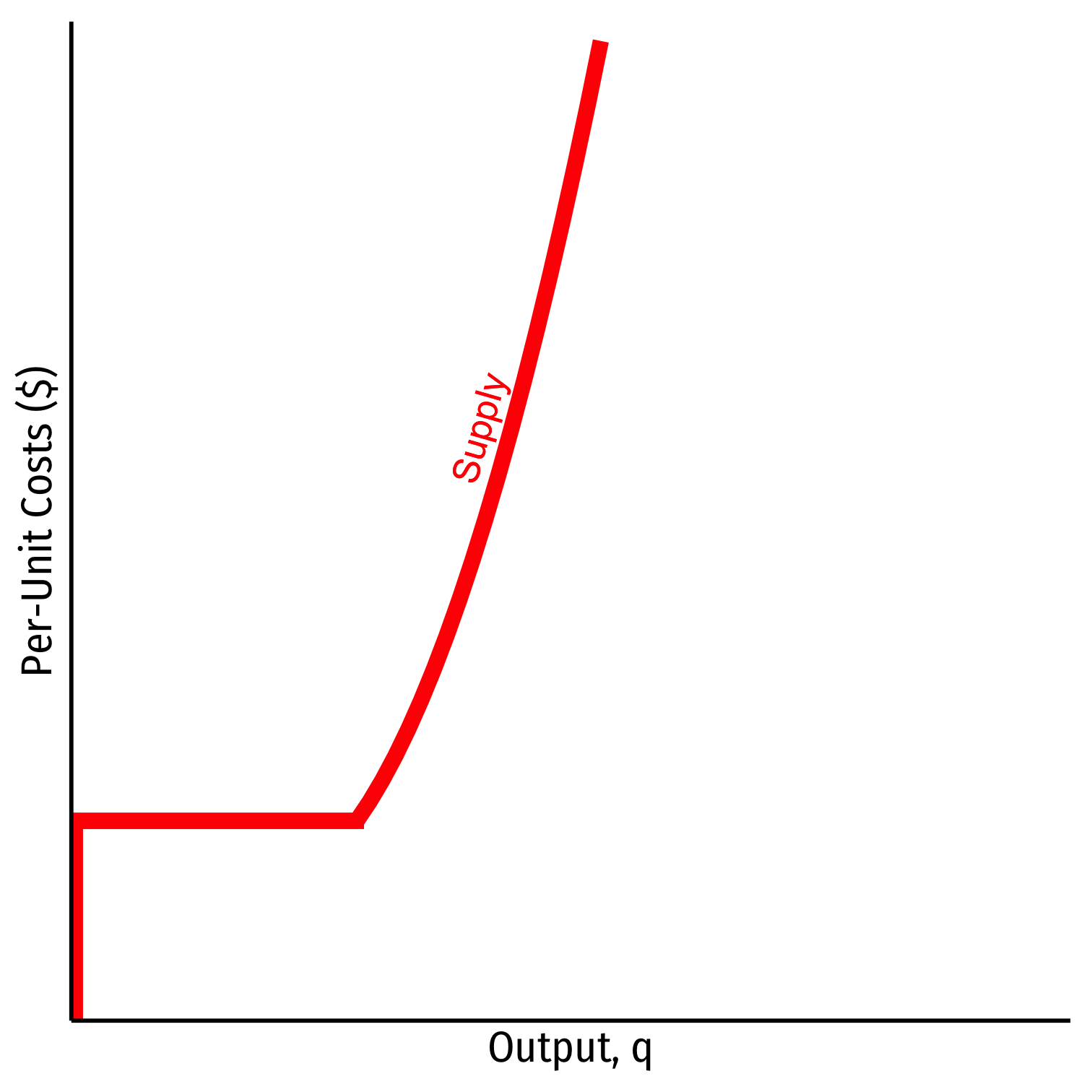
Firm’s short run supply curve:
Summary:
1. Choose q∗ such that MR(q)=MC(q)
Summary:
1. Choose q∗ such that MR(q)=MC(q)
2. Profit π=q[p−AC(q)]
Summary:
1. Choose q∗ such that MR(q)=MC(q)
2. Profit π=q[p−AC(q)]
3. Shut down if p<AVC(q)
Summary:
1. Choose q∗ such that MR(q)=MC(q)
2. Profit π=q[p−AC(q)]
3. Shut down if p<AVC(q)
Firm's short run (inverse) supply:
{p=MC(q)if p≥AVCq=0If p<AVC