1.8 — Factor Markets
ECON 326 • Industrial Organization • Spring 2023
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/ioS23
ioS23.classes.ryansafner.com
Returning to Firms
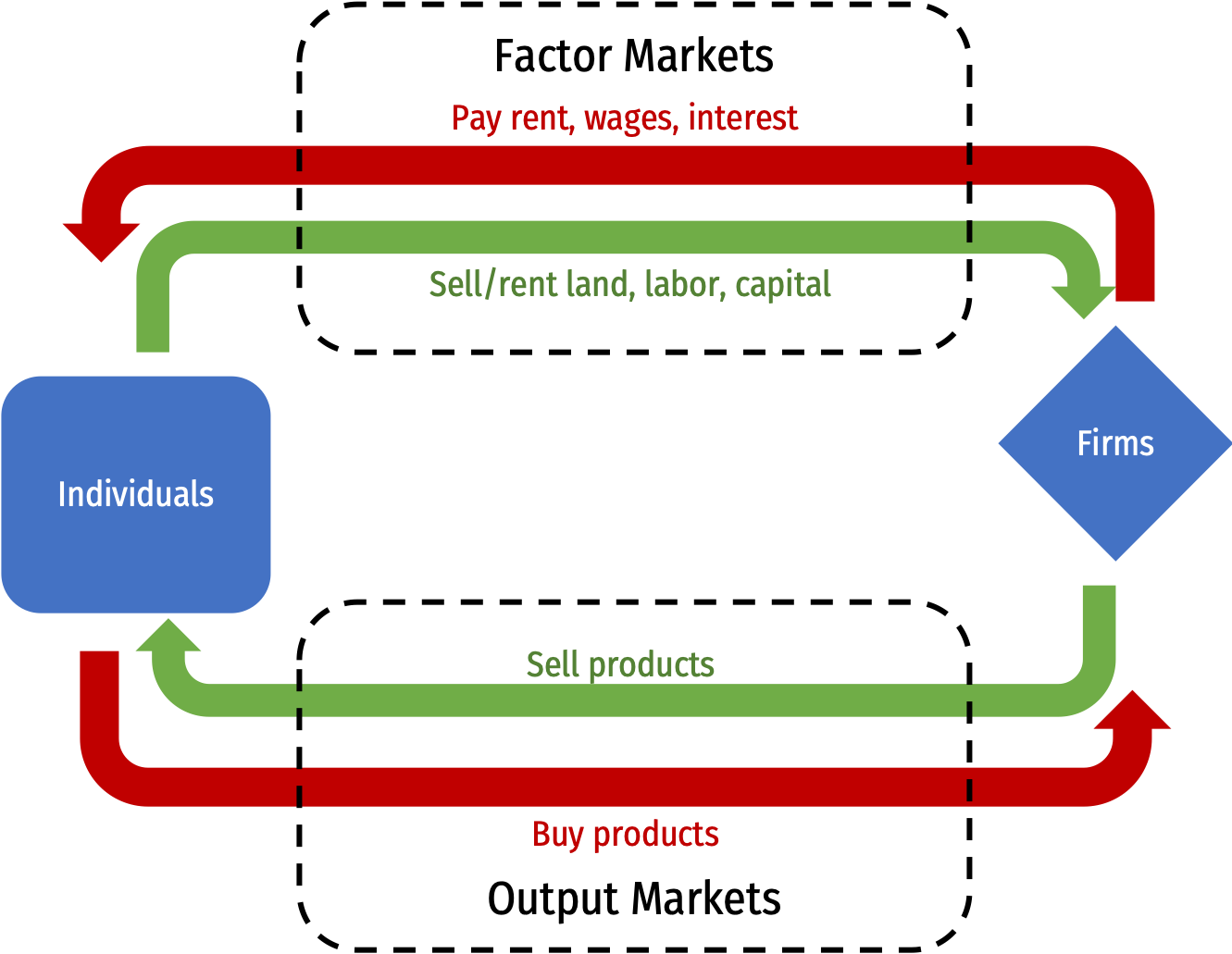
Recall a firm uses technology that buys inputs, transforms them, and sells output $$q=f(k,l)$$
- We classified inputs into the factors of production: land, labor, capital
We assumed fixed factor prices
- show up in total cost \(=wL+rK\)
Where do they come from? Factor markets
Circular Flow
Firms’ Payments to Factors are Income To Households
| Income Type | Amount (2016) | Percent |
|---|---|---|
| Salaries and wages | $7217 Bn | 68.45% |
| Taxable pensions and annuities | $694 Bn | 6.58% |
| Partnership and S corporation net income | $629 Bn | 5.97% |
| Capital gains less losses | $621 Bn | 5.89% |
| Business net income | $389 Bn | 3.69% |
| Taxable Social Security benefits | $286 Bn | 2.71% |
| Taxable IRA distributions | $258 Bn | 2.45% |
| Ordinary dividends | $254 Bn | 2.41% |
| Total rental and royalty net income | $98 Bn | 0.93% |
| Taxable interest | $97 Bn | 0.92% |
Source: Tax Foundation, 2018
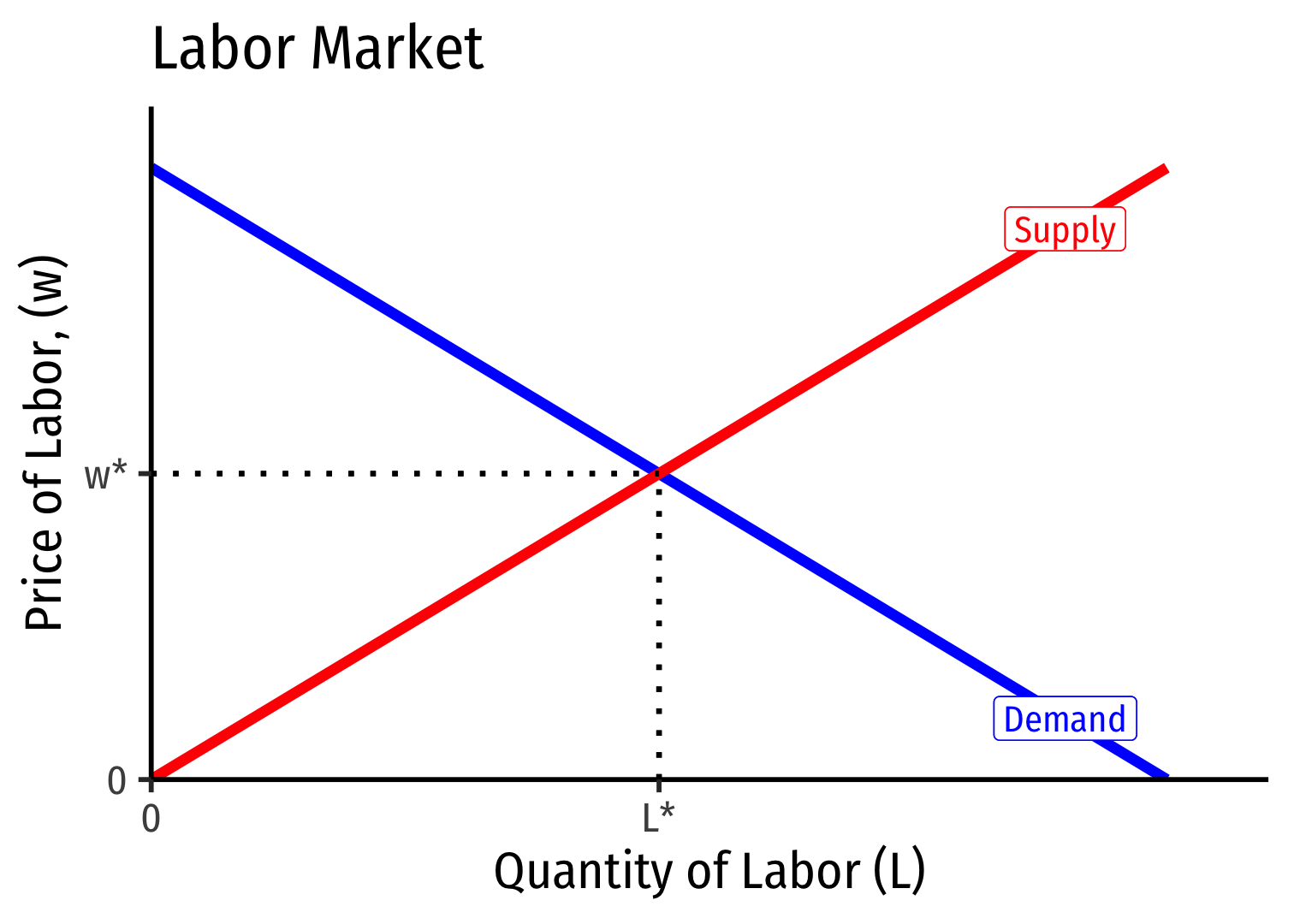
Supply and Demand in Factor Markets
The price of a factor is governed by the same market forces as output:
Supply of Factor: willingness of factor owners to accept and sell/rent their services to firms
- landowners, workers, capitalists, resource owners, suppliers
Demand for Factor: willingness of firms to pay for/hire factor services

Factor Market Prices and Opportunity Costs
- Factor price represents opportunity cost of hiring a factor for an alternative use
- Firms not only pay for direct use of a factor, but also indirectly for not using it in an alternate process!

Factor Market Prices and Opportunity Costs
- Example: a producer of hammers buys steel, pays (the opportunity cost) for "taking" the steel away from alternative uses

Factor Market Prices and Opportunity Costs
- Example: e.g. salary for a skilled worker must be high enough to keep them at their current firm, and not be attracted to other firms/industries

Example Factor Market: Labor Markets
Empirically, about 70% of total cost of production comes from labor
We’ll focus just on the market for labor as an example factor market
Can do the same for any factor market
- (e.g. capital, land, materials, etc.)

Labor Supply Decisions
Labor Supply Decisions
The Supply of Labor comes from individual decisions to work
Labor is considered a disutility (a bad)
- Opportunity cost of labor is leisure
- But, labor generates income for consumption (a good)
Tradeoff: if you work more, you get more income, but less leisure


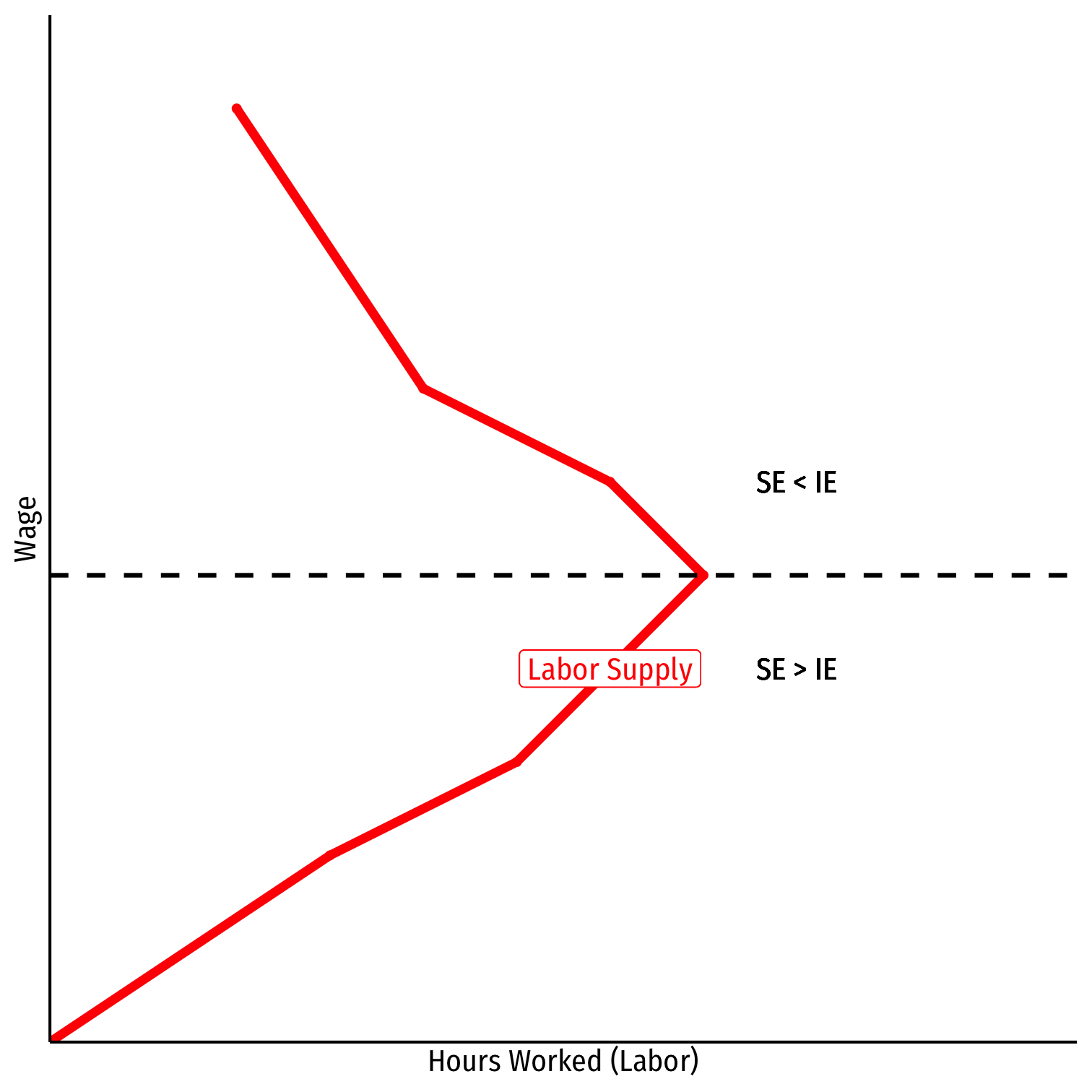
Modeling Labor Supply Decisions: A Change In Wages
We often see “backward-bending” labor supply curves
Depends on whether income or substitution effect dominates
A Brief Digression on Economic Rents I
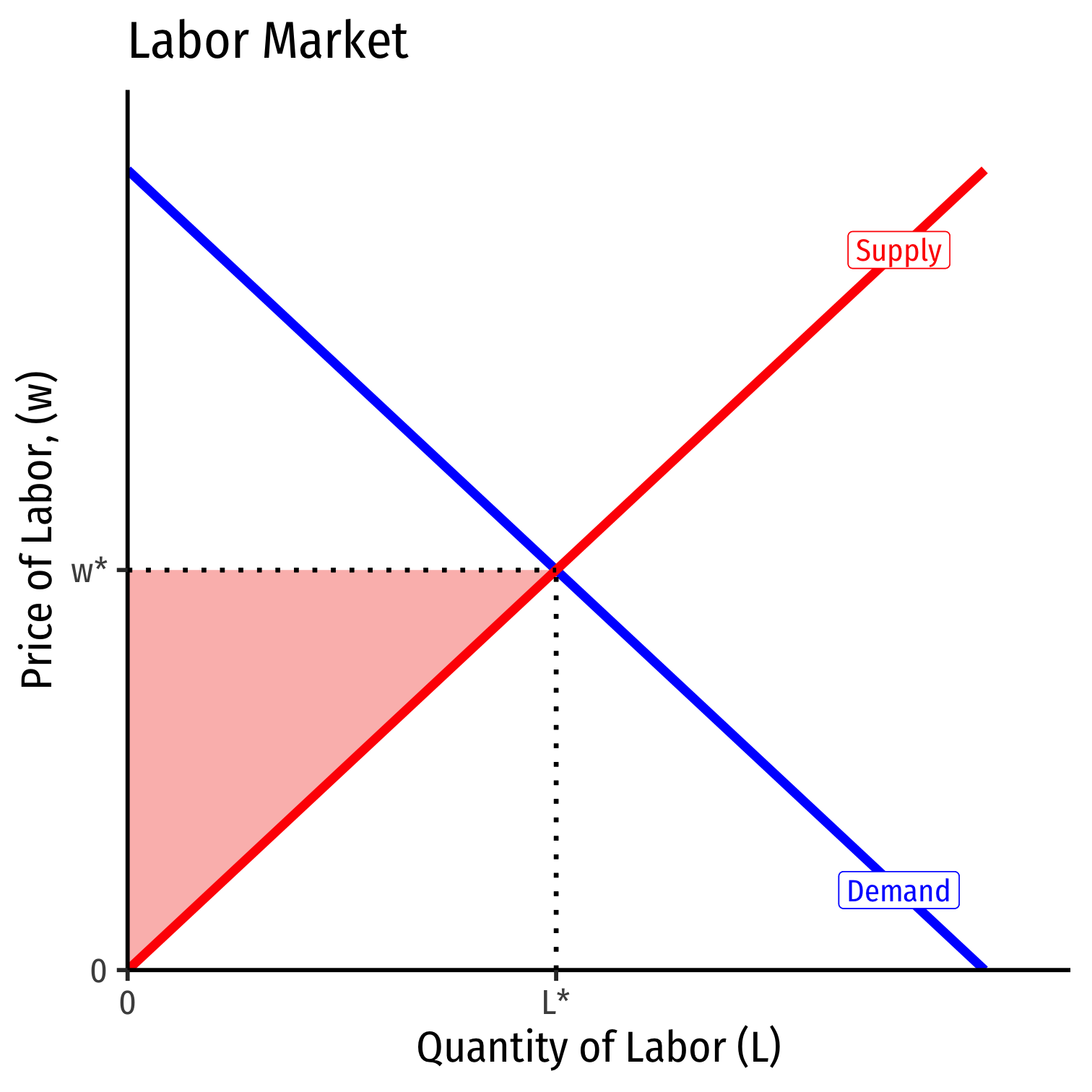
Recall market supply is the minimum willingness to accept, the minimum price necessary to bring a resource to market (its opportunity cost)
But all (equivalent) labor is paid the market wage, \(w^*\) determined by market labor supply and labor demand
A Brief Digression on Economic Rents II
Some workers would have accepted a job for less than \(w^*\)
These inframarginal workers earn economic rent in excess of what is needed to bring them into the market (their opportunity cost)
A Brief Digression on Economic Rents III
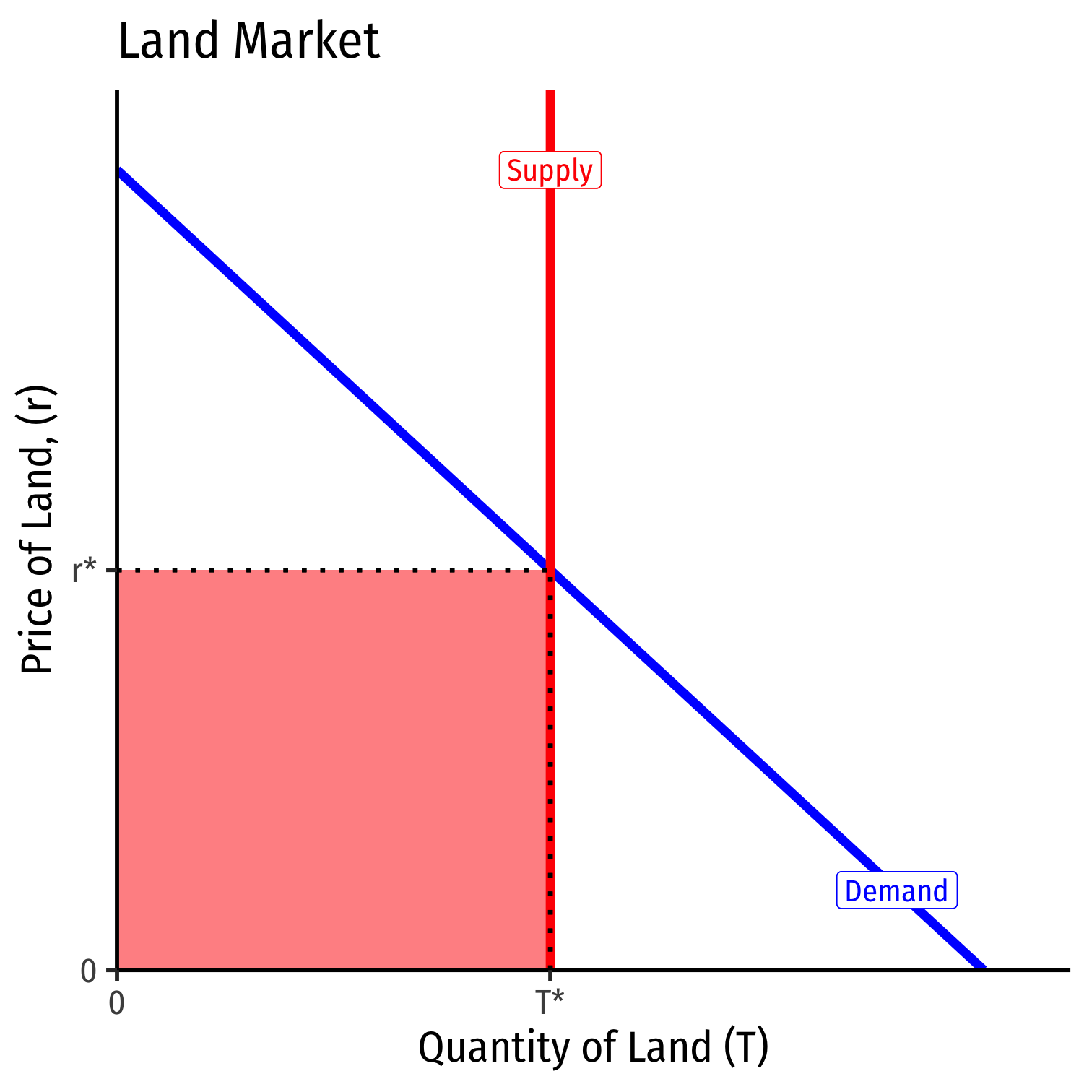
Consider a factor (such as land) for which the supply is perfectly inelastic (e.g. a fixed supply)
Then the entire value of the land is economic rent!
The less elastic the supply of a factor, the more economic rent it generates!
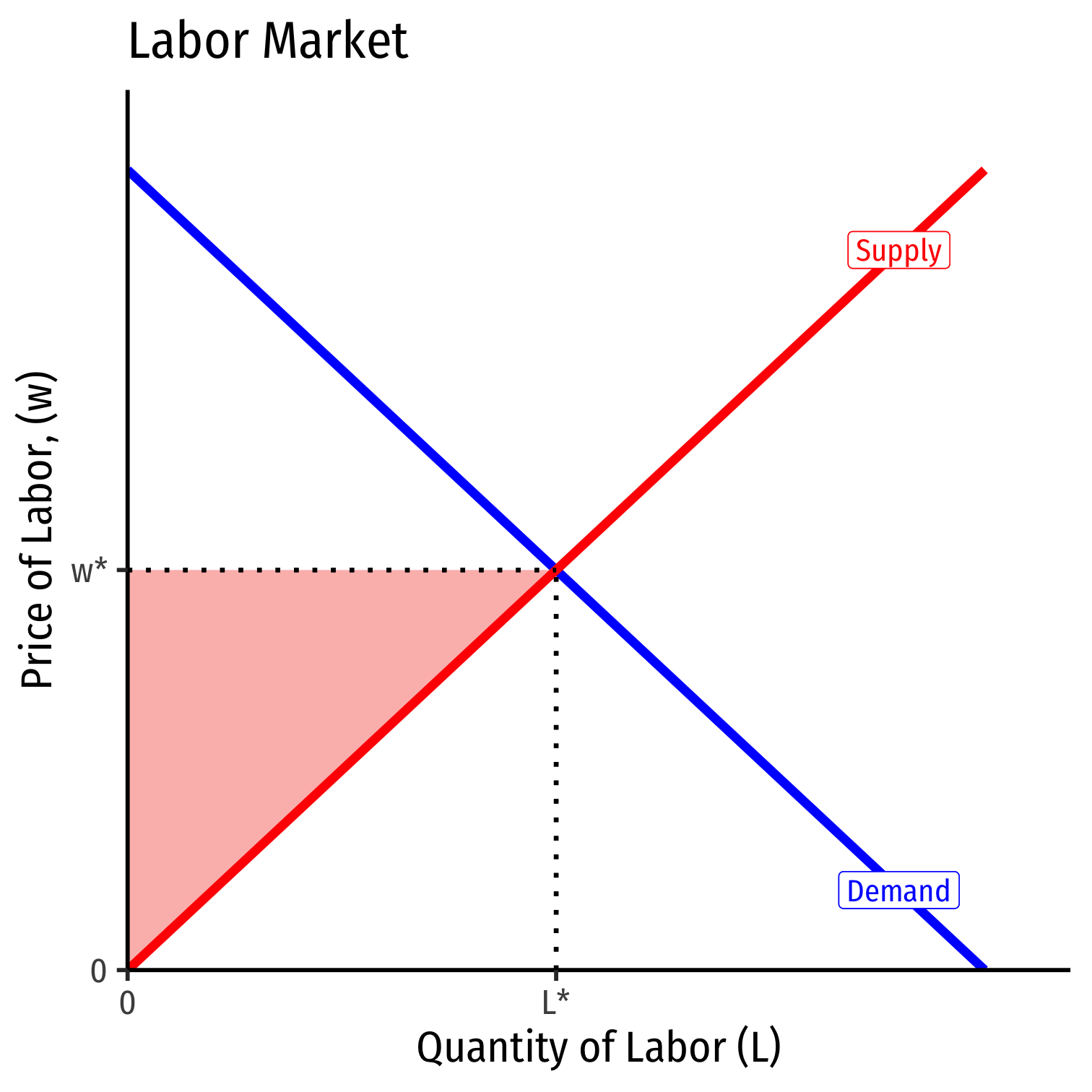
Labor Market for a Competitive Firm
Derived Demand in Factor Markets
Demand for factors is a “derived demand”:
- Firm only demands inputs to the extent they contribute to producing sellable output
Firm faces a tradeoff when hiring more labor, as more labor \(\Delta L\) creates:
- Marginal Benefit: Increases output and thus revenue
- Marginal Cost: Increases costs

Marginal Revenue Product (of Labor)
- Hiring more labor increases new output (i.e. labor's \(MP_L\))
- Recall: \(MP_L=\frac{\Delta q}{\Delta L}\), where \(q\) is units of output
Marginal Revenue Product (of Labor)
Hiring more labor increases new output (i.e. labor's \(MP_L\))
- Recall: \(MP_L=\frac{\Delta q}{\Delta L}\), where \(q\) is units of output
Additional output generates new revenues (i.e. labor's \(MR(q)\))
- Recall: \(MR(q)=\frac{\Delta R(q)}{\Delta q}\), where \(R(q)\) is total revenue
Marginal Revenue Product (of Labor)
Hiring more labor increases new output (i.e. labor's \(MP_L\))
- Recall: \(MP_L=\frac{\Delta q}{\Delta L}\), where \(q\) is units of output
Additional output generates new revenues (i.e. labor's \(MR(q)\))
- Recall: \(MR(q)=\frac{\Delta R(q)}{\Delta q}\), where \(R(q)\) is total revenue
- Hiring more labor, on the margin, generates a benefit, called the marginal revenue product of labor, \(MRP_L\):
$$MRP_L=MP_L* MR(q)$$
- i.e. the number of new products a new worker makes times the revenue earned by selling the new products
Marginal Revenue Product for Competitive Firms
- This is the Firm's Demand for Labor:
$$MRP_L=MP_L* MR(q)$$
- For a firm in a competitive (output) market, firm's \(MR(q)=p\), hence:
$$MRP_L=MP_L*p$$ where \(p\) is the price of the firm's output
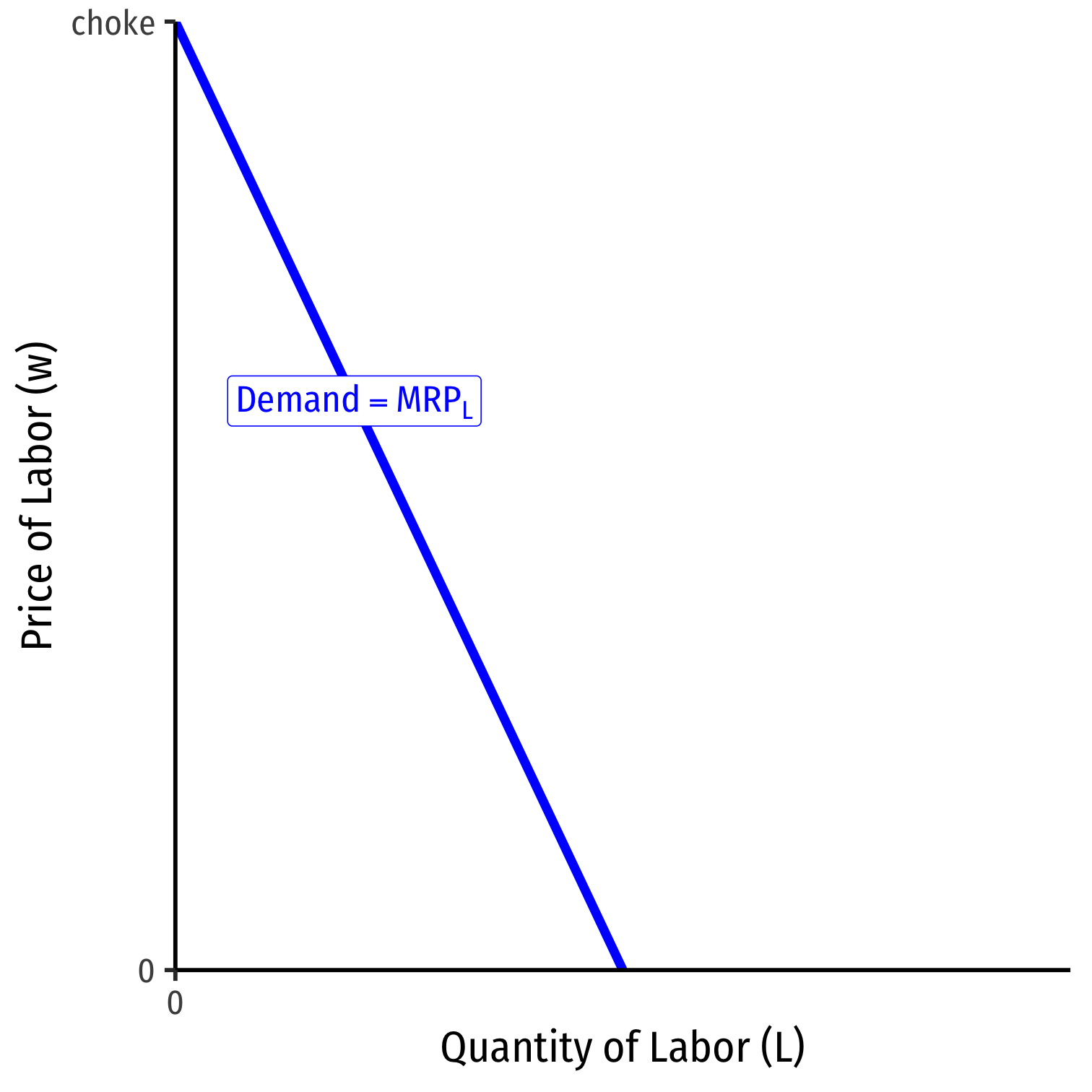
Marginal Revenue Product for Competitive Firms
$$MRP_L=MP_L* p$$
Marginal benefit of hiring labor, \(MRP_L\) falls with more labor used
- production exhibits diminishing marginal returns to labor!
Choke price for labor demand: price too high for firm to purchase any labor
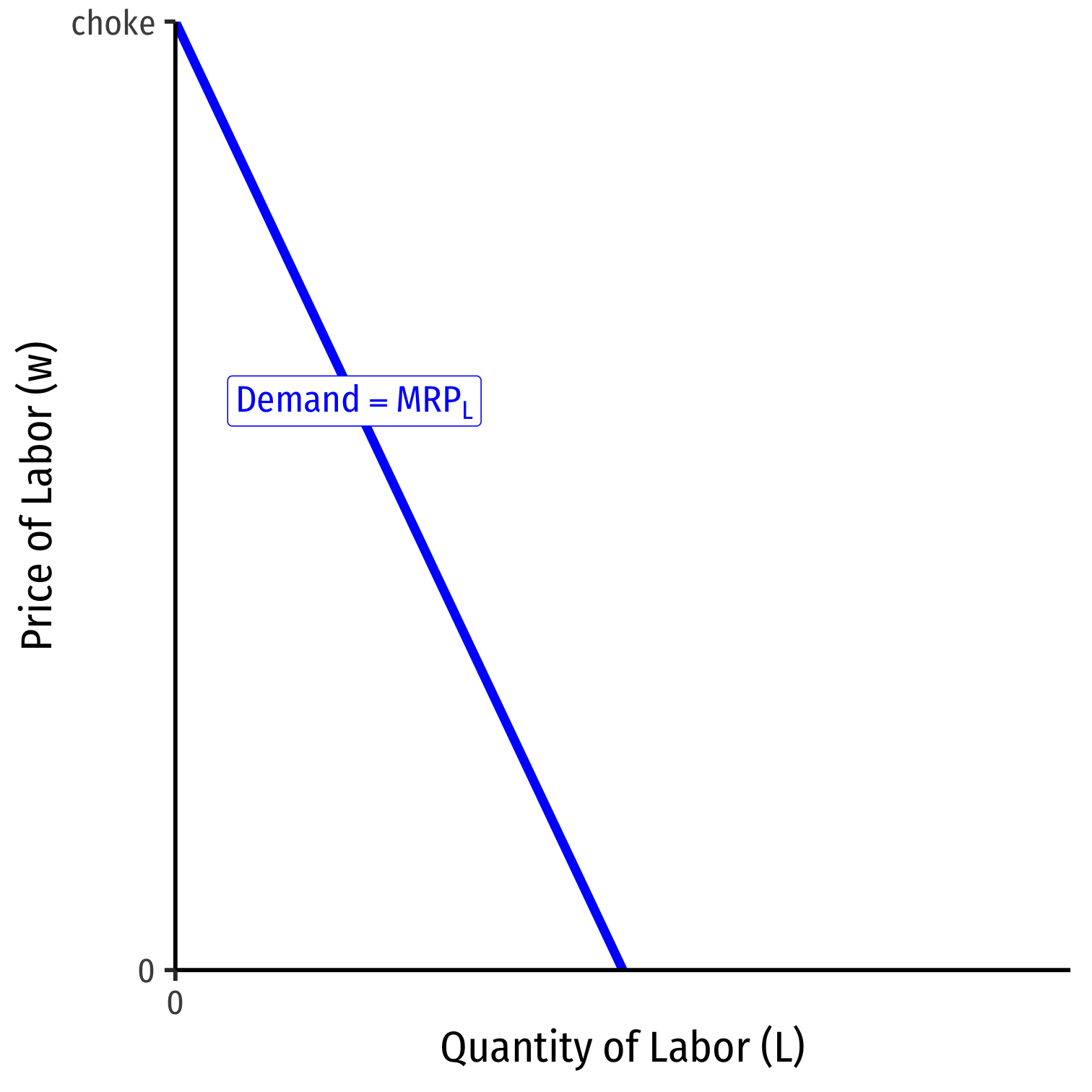
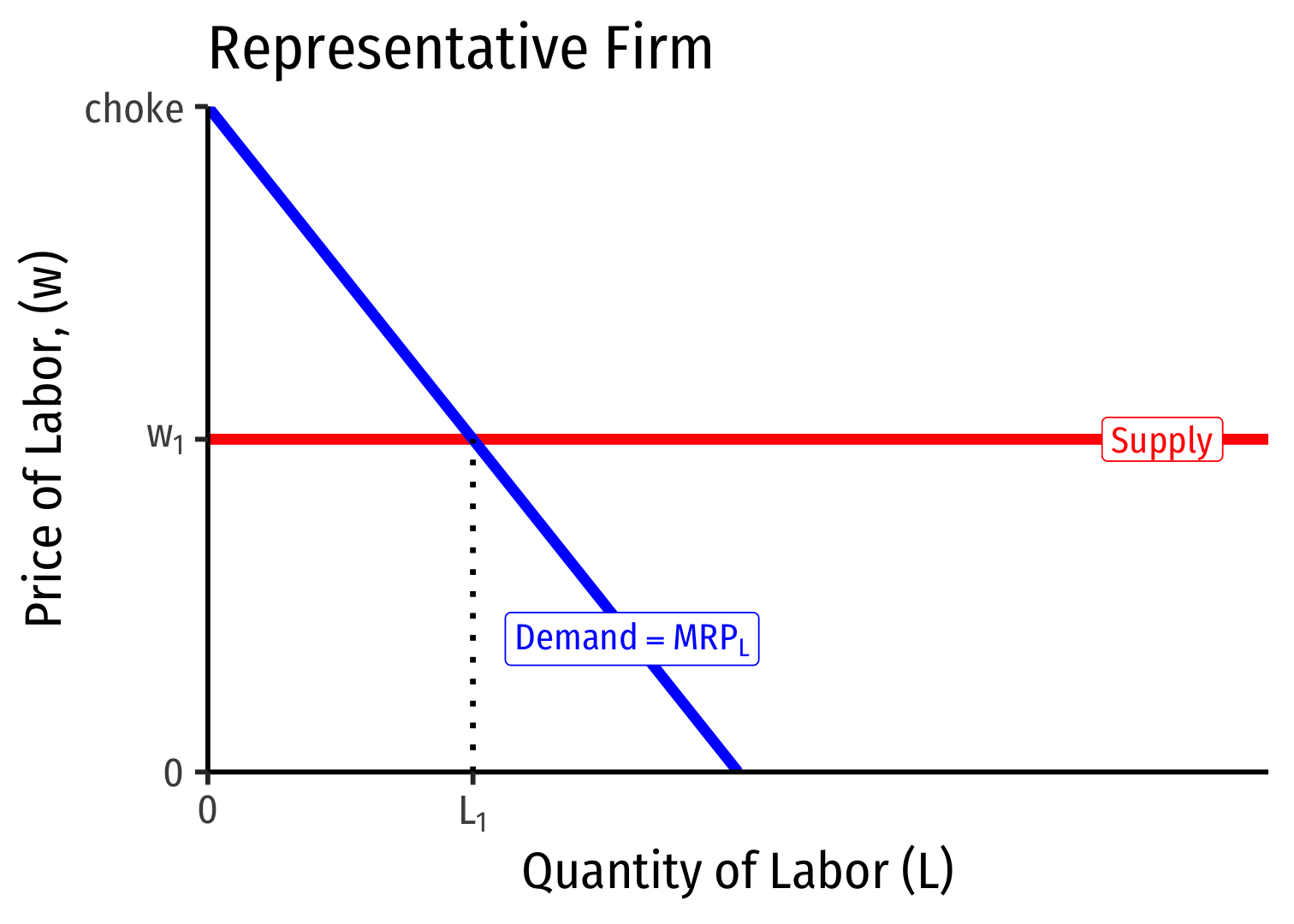
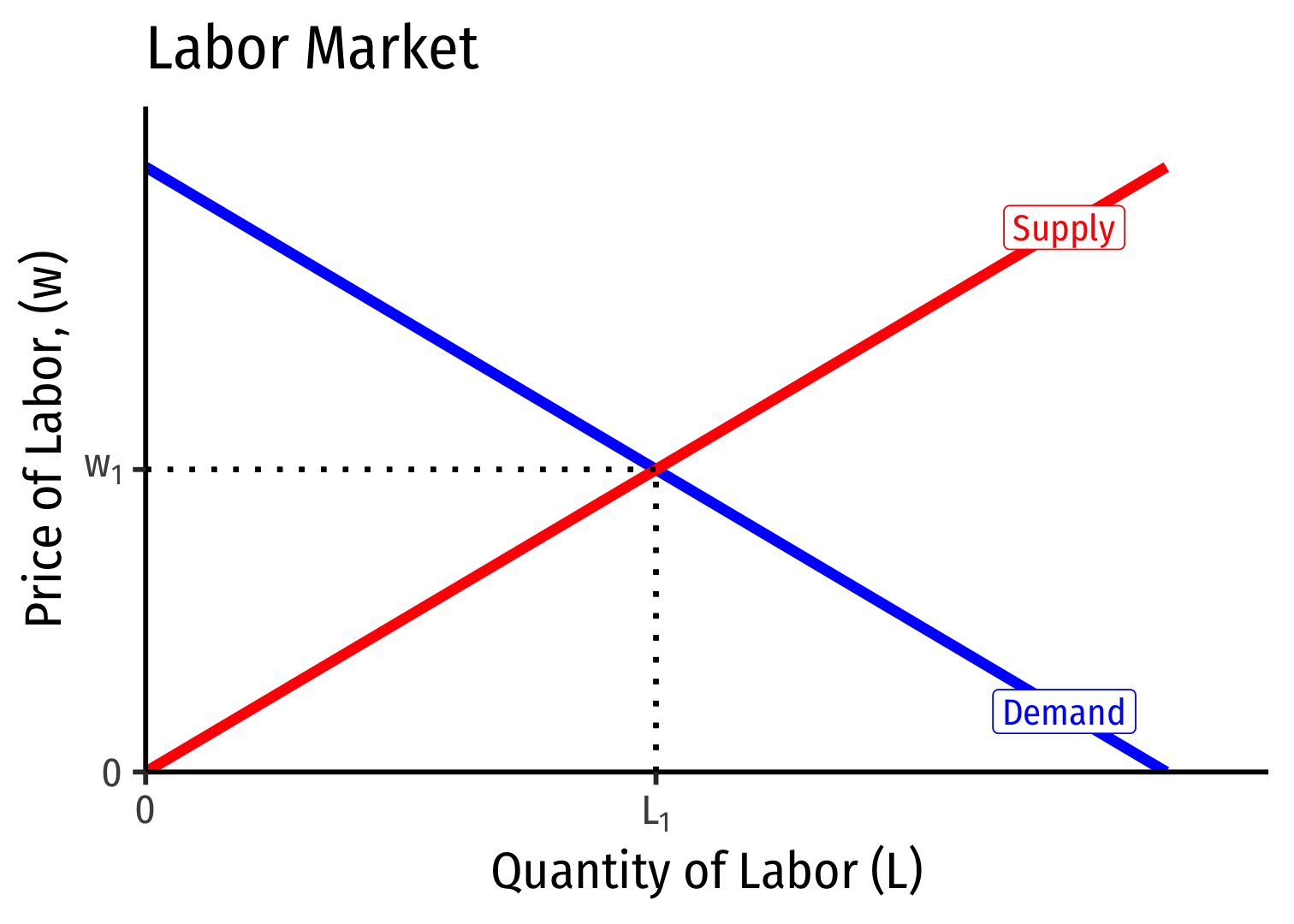
A Competitive Factor Market
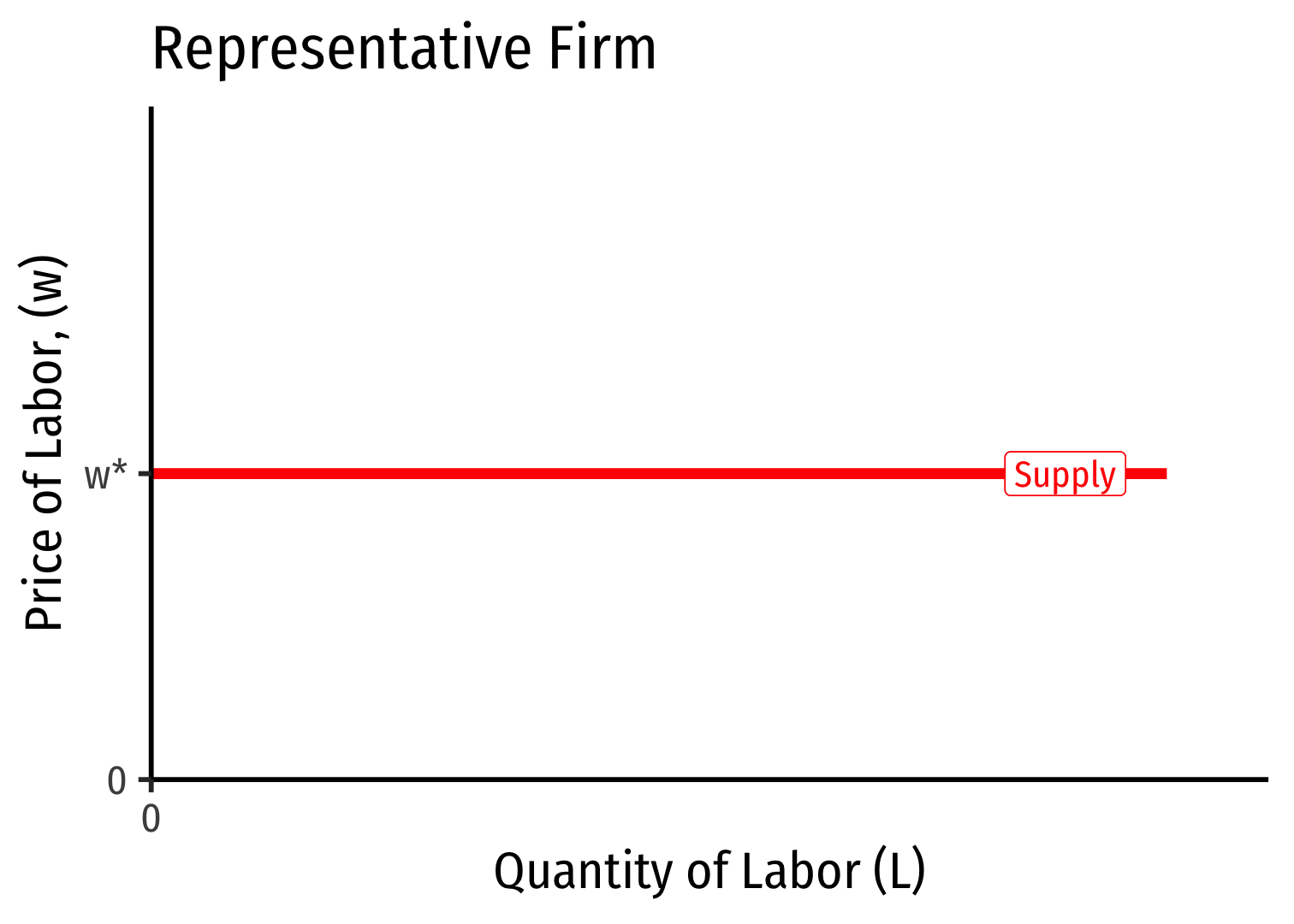
- If the factor market is competitive, labor supply available to an individual firm is perfectly elastic at the market price of labor \((w^*)\)
Labor Supply and Firm's Demand for Labor
We've seen a falling \(MRP_L\), the marginal benefit of hiring labor
Marginal cost of hiring labor, \(w\), remains constant
- so long as firm is not a big purchaser (has no market power) in the labor market
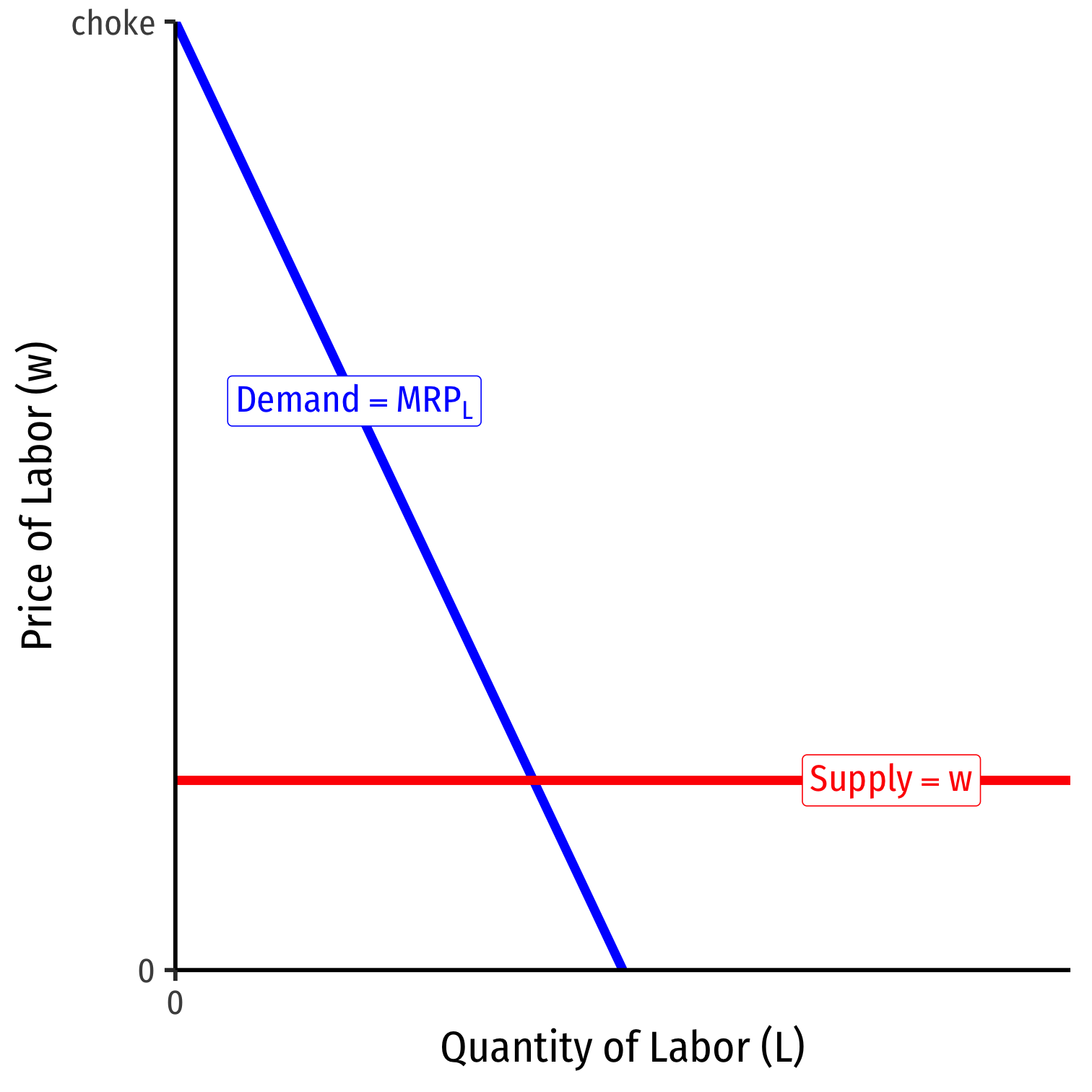
Labor Supply and Firm's Demand for Labor
At low amounts of labor, marginal benefit \(\color{#0047AB}{MRP_L} > \color{#D7250E}{w}\) marginal cost
Firm will hire more labor
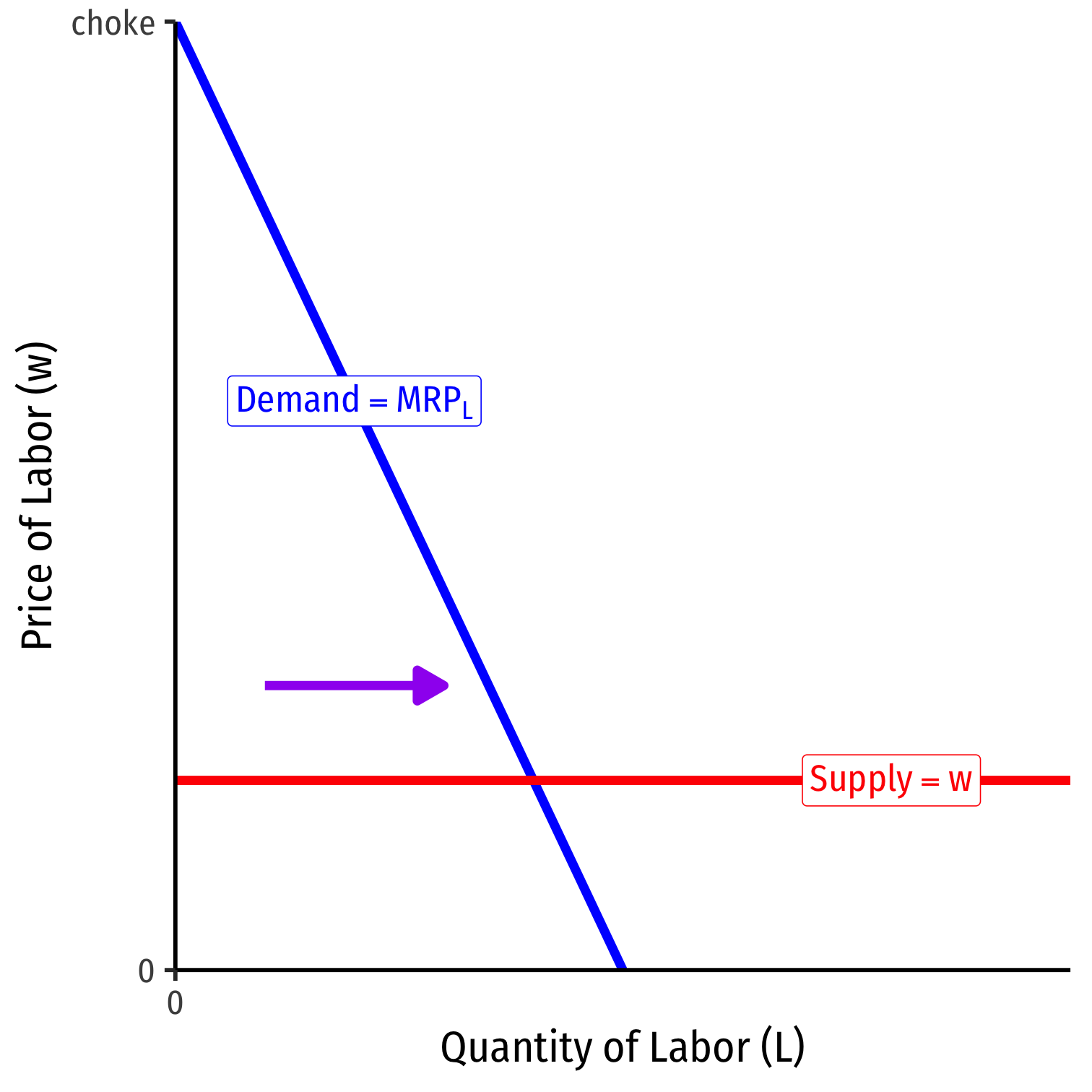
Labor Supply and Firm's Demand for Labor
At high amounts of labor, marginal benefit \(\color{#0047AB}{MRP_L} < \color{#D7250E}{w}\) marginal cost
Firm will hire less labor
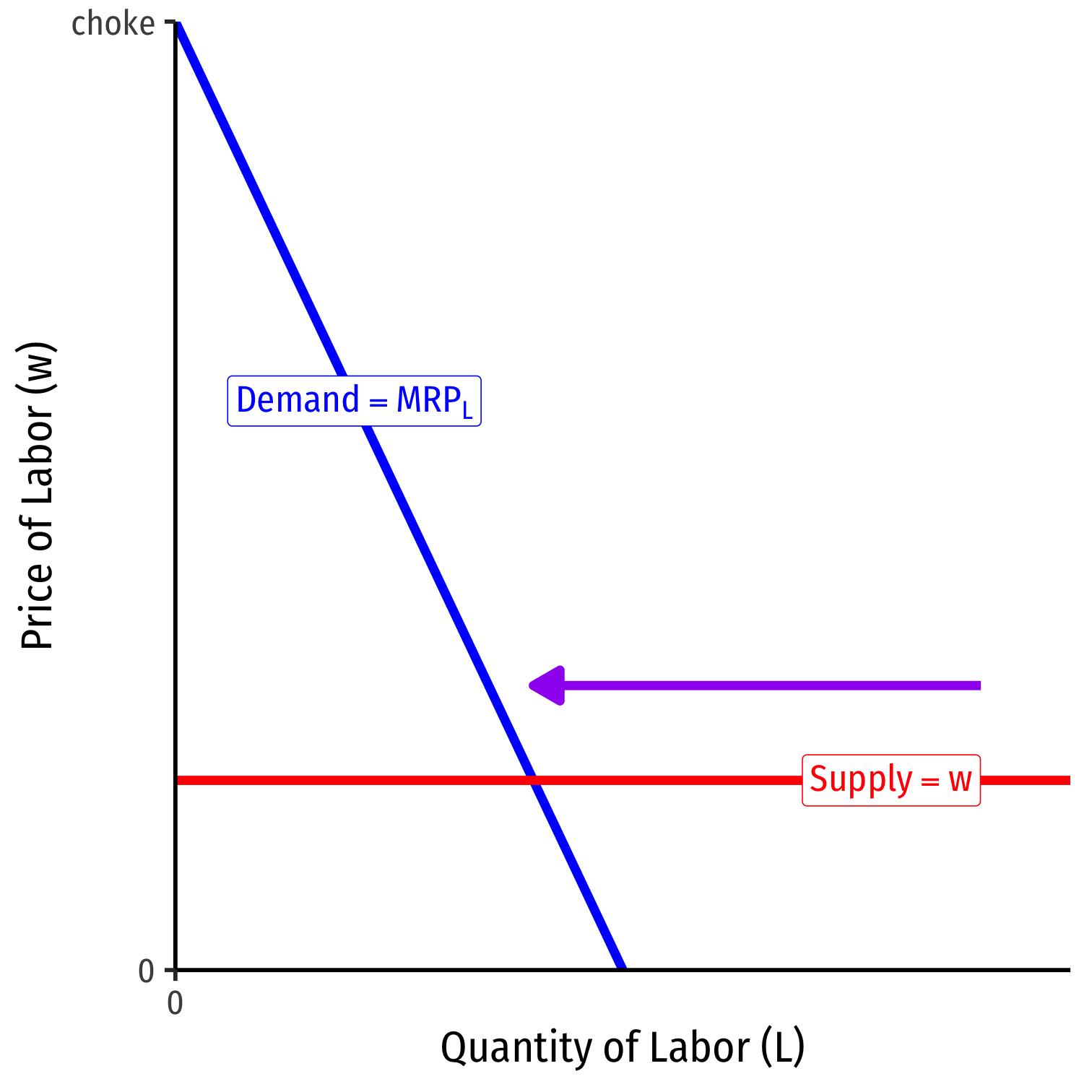
Labor Supply and Firm's Demand for Labor
Firm hires \(L^*\) optimal amount of labor where \(w=MRP_L\)
i.e. marginal cost of labor \(=\) marginal benefit of labor
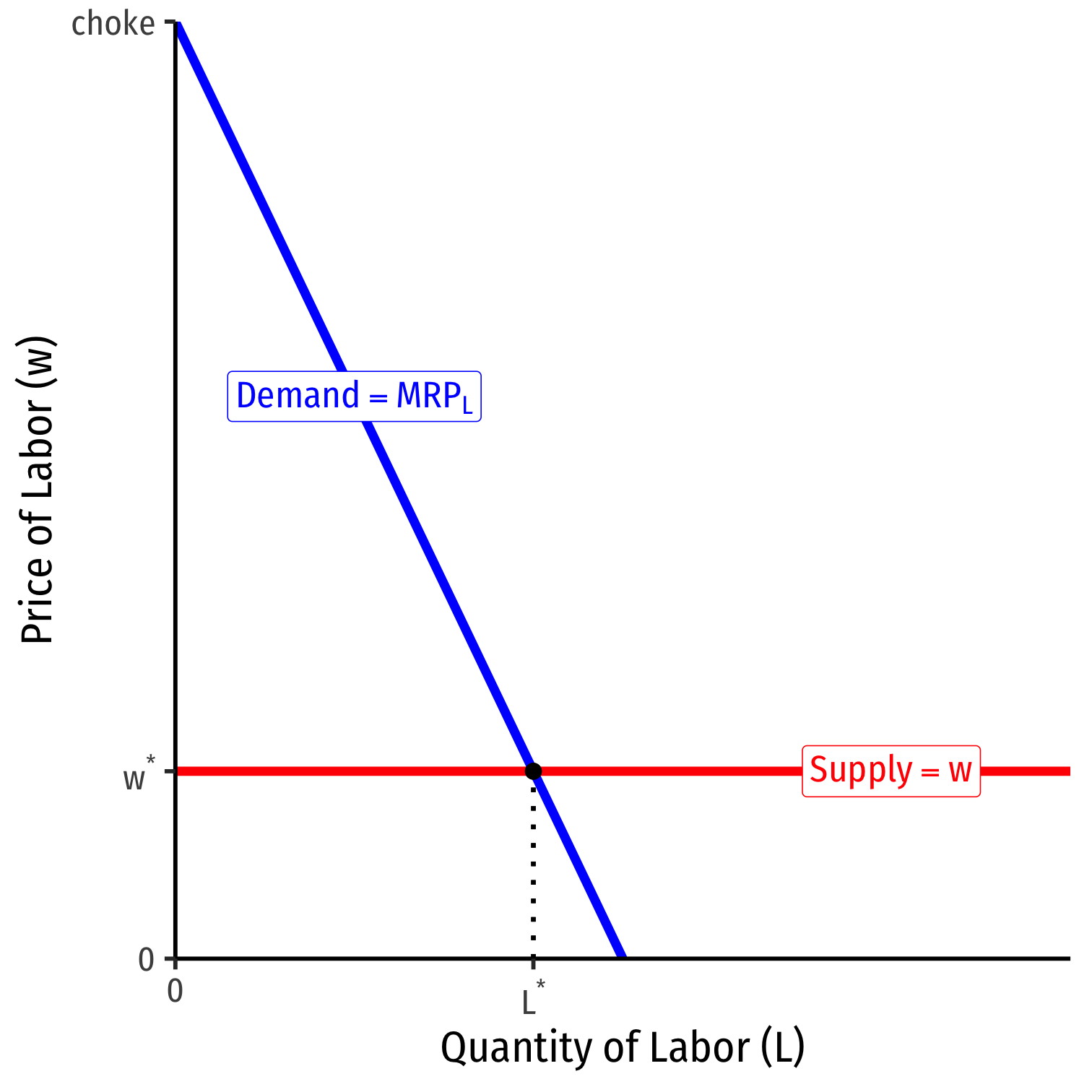
Labor Supply and Firm's Demand for Labor
Labor Supply and Firm's Demand for Labor
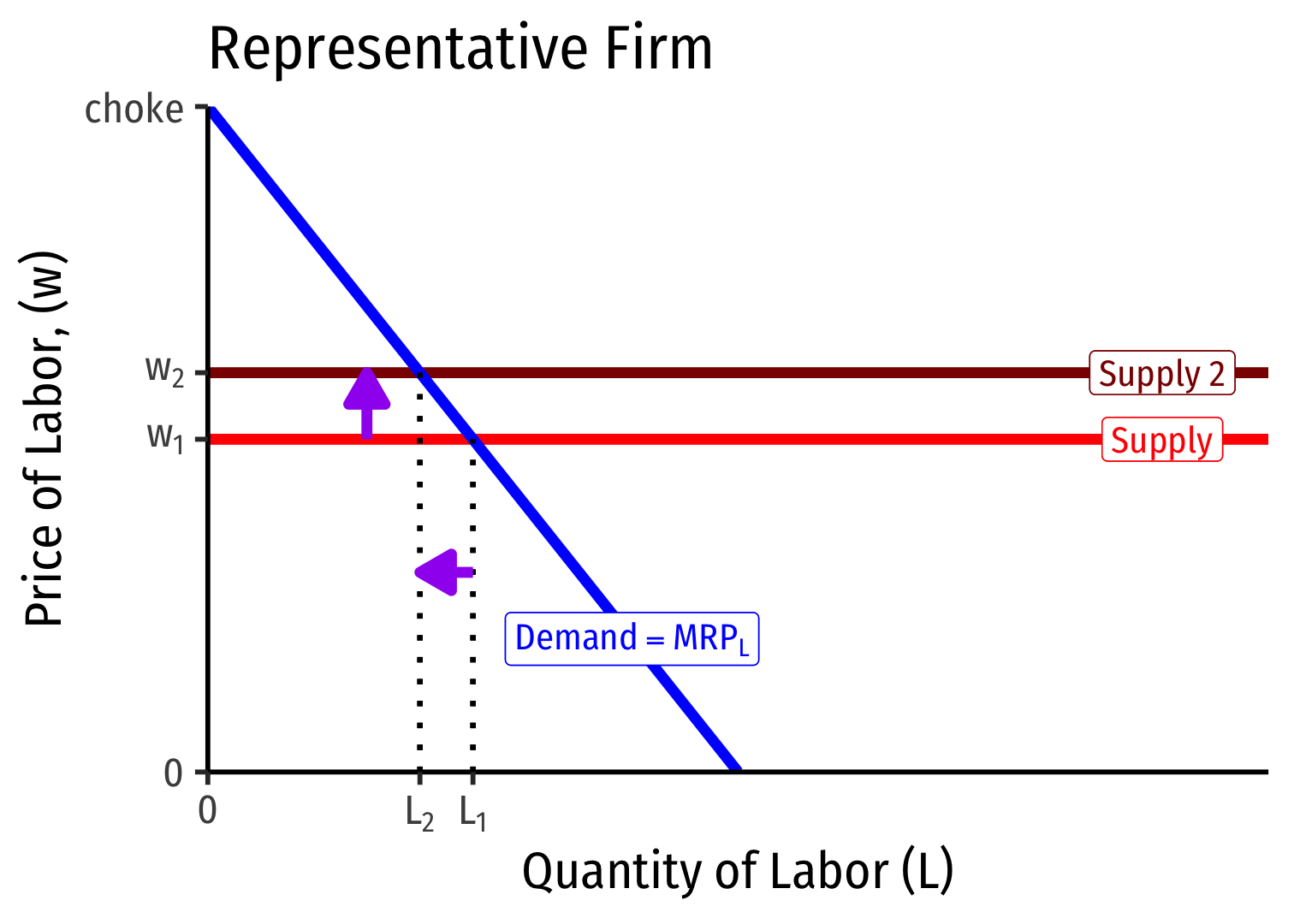
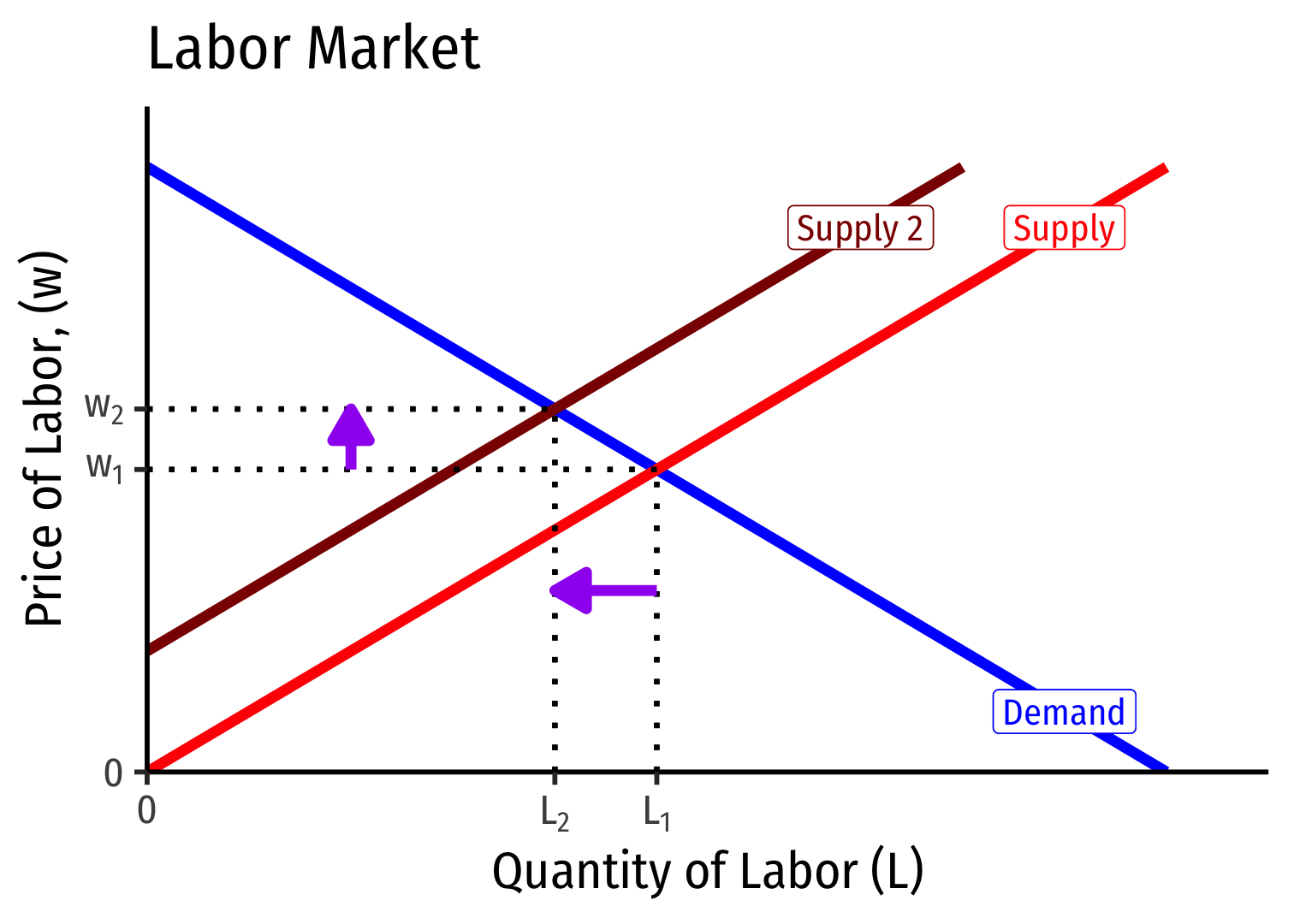
- If market supply of labor decreases (increases), wages increase (decrease) & firms hire fewer (more) workers
Example
Example: Victoria’s Tours is a travel company that offers guided tours of nearby mountain biking trails. Its marginal revenue product of labor is given by $$MRP_L = 1,000 – 40L$$
where \(L\) is the number of tour-guide weeks it hires and \(MRP_L\) is measured in dollars per tour-guide week. The going market wage for tour guides is $600 per tour-guide week.
What is the optimal amount of labor for Victoria’s Tours to hire?
At and above what market wage would Victoria’s Tours not want to hire any labor?
What is the most labor Victoria’s Tours would ever hire, given its marginal revenue product?
Labor Demand for a Monopoly
Labor Demand for Competitive vs. Monopolist Firm
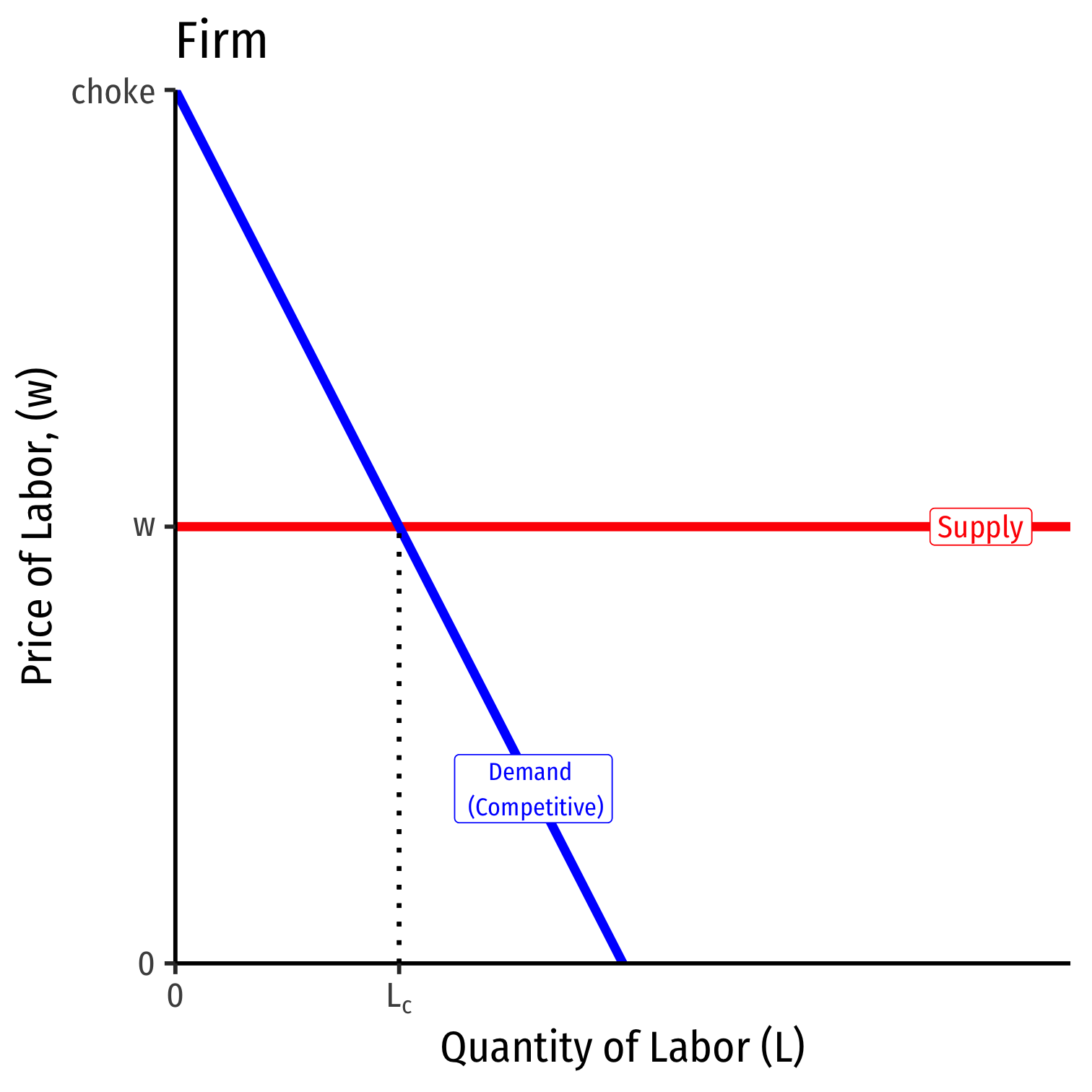
Recall a firm's demand for labor: \(\color{blue}{MRP_L= MP_L * MR(q)}\)
A firm in a competitive output industry has its \(MR(q)=p\)
- So we saw its Labor Demand, \(MRP_L = MP_L * p\)
Labor Demand for Competitive vs. Monopolist Firm
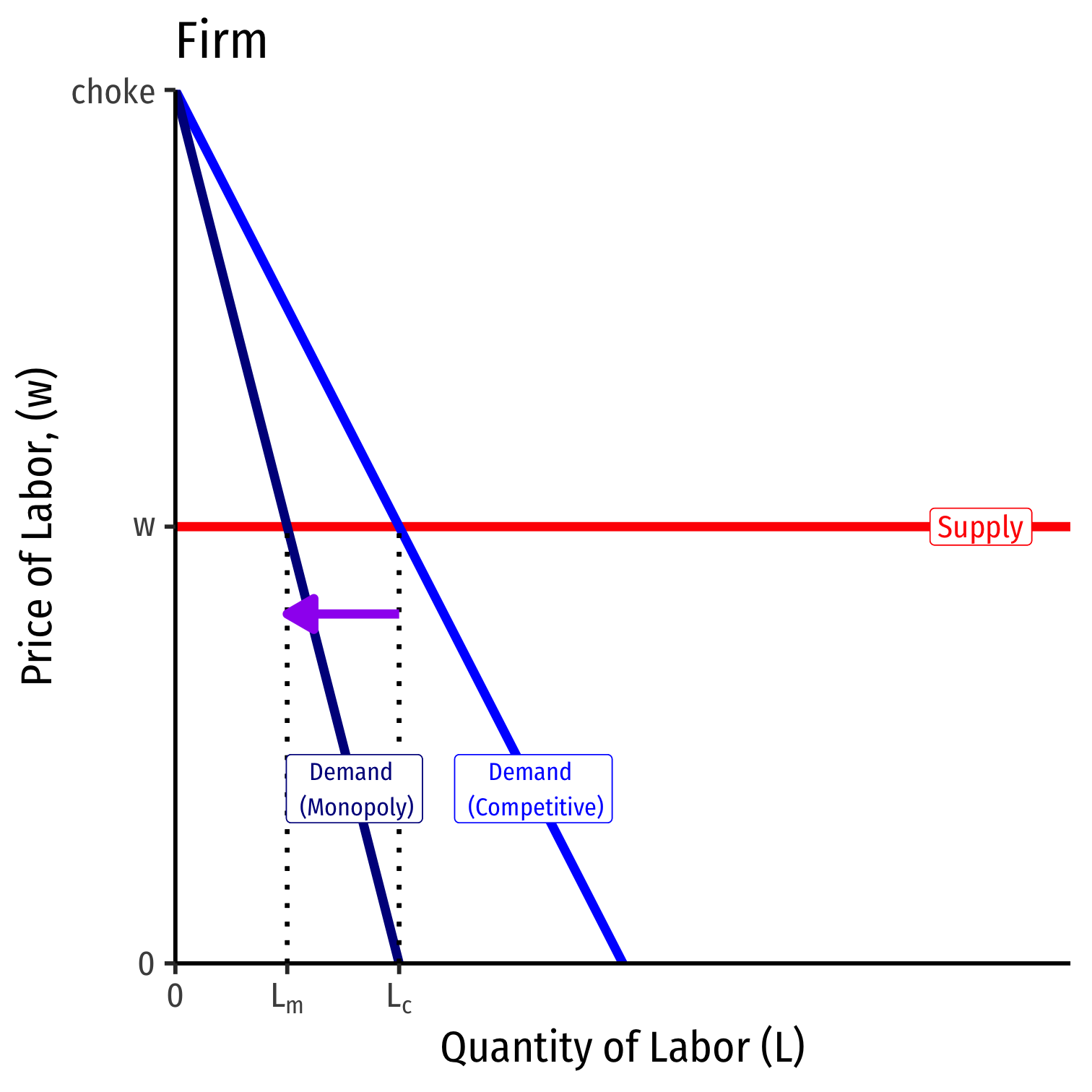
Recall if firm is a monopolist in its output industry, its \(MR(q) < p\)
- So its Labor Demand, \(MRP_L = MRP_L * MR(q)\)
Since \(MR(q) < p\), a monopoly in its output industry will always have lower demand for labor, and thus, hire less labor than a competitive firm
- Monopoly produces less output, so wants fewer inputs!
Labor Demand for Competitive vs. Monopolist Firm
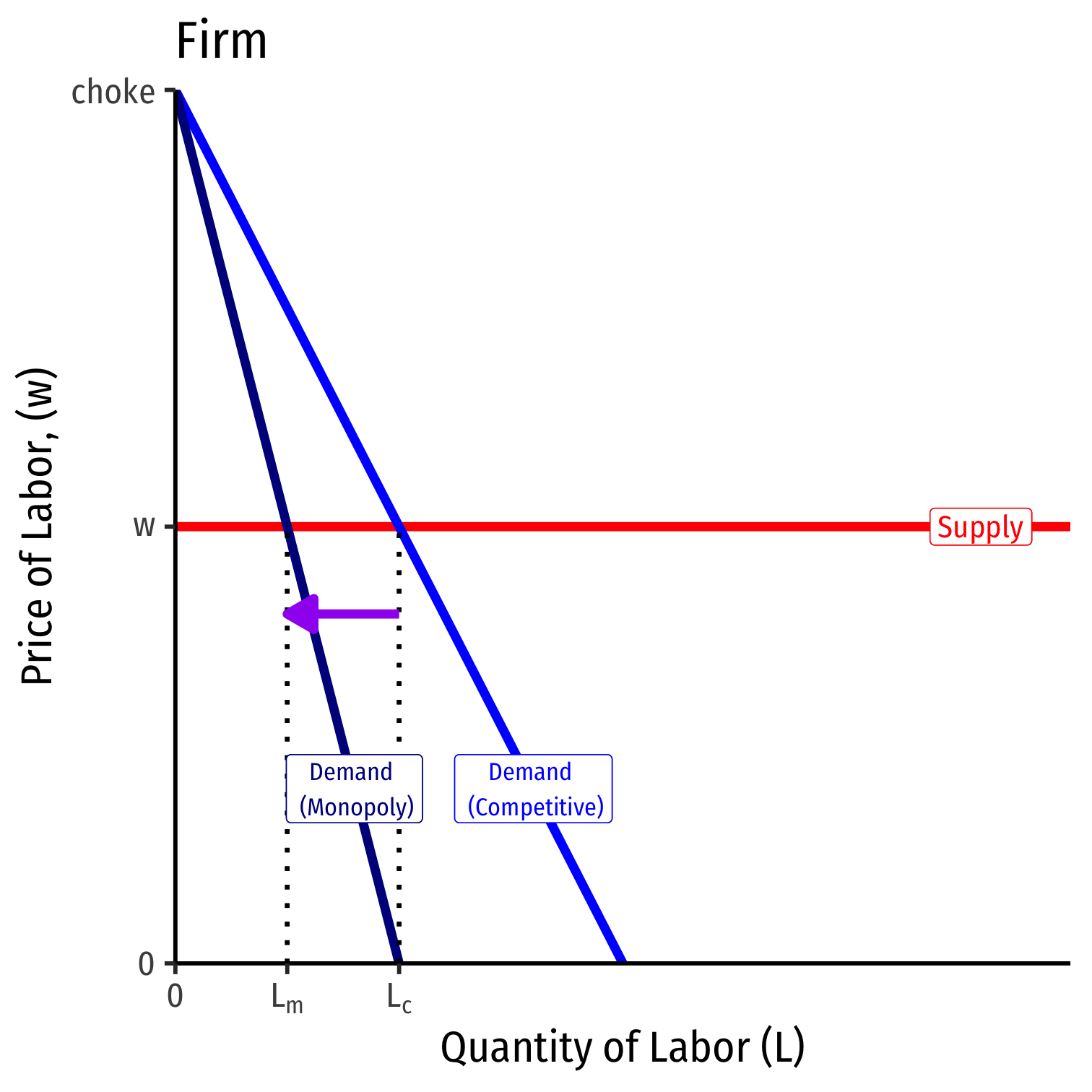
This is about the competitiveness of the output or “downstream” market
Here, both competitive firm and monopolist in downstream markets face the same perfectly elastic labor supply
- We've assumed no market power in the input or “upstream” market (for labor)
We next consider market power in the upstream (labor) market...
Monopsony Power
Monopsony
What if the firm has market power in a factor market?
Consider extreme example: monopsony: a factor market with a single buyer

Monopsony and Market Supply of Labor
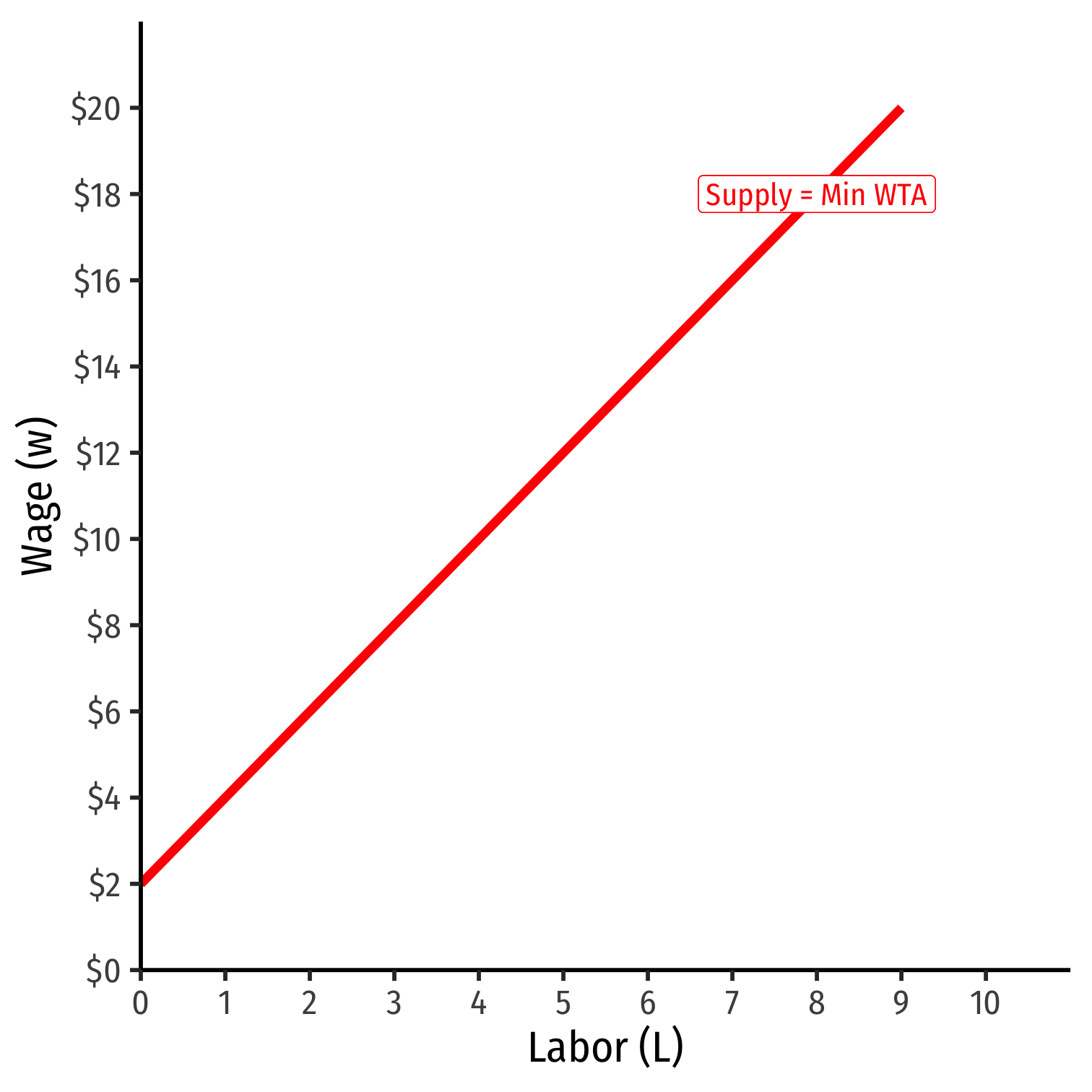
Market power in hiring labor implies that the firm faces the whole market factor supply curve for labor
Market supply is upward sloping
Factor (inverse) supply describes minimum price workers are willing to accept to work
Monopsony and Market Supply of Labor
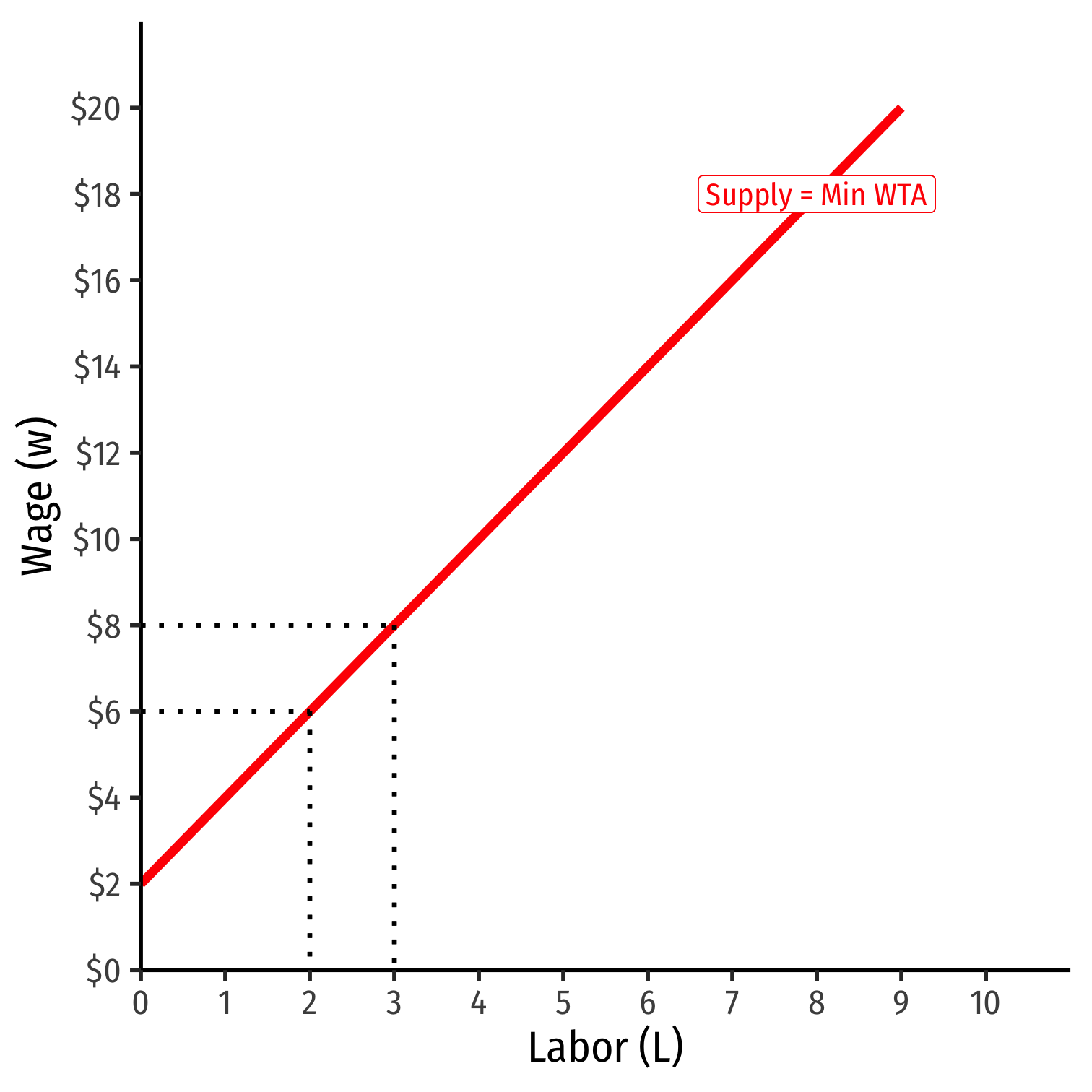
- As firm chooses to hire more \(L\), must raise wages on all workers to hire them
Monopsony and Market Supply of Labor
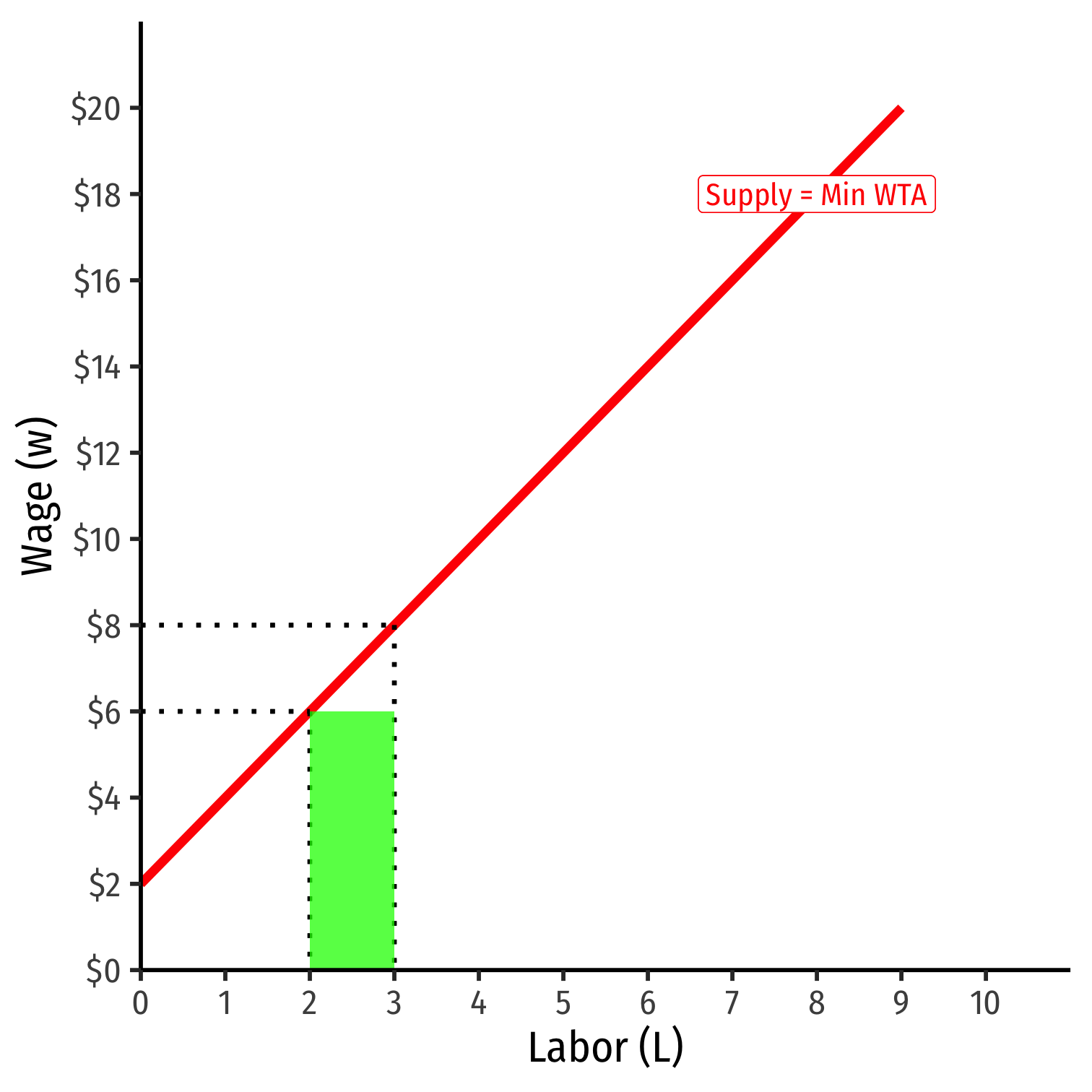
As firm chooses to hire more \(L\), must raise wages on all workers to hire them
Output effect: increased cost from increased number of workers
Monopsony and Market Supply of Labor
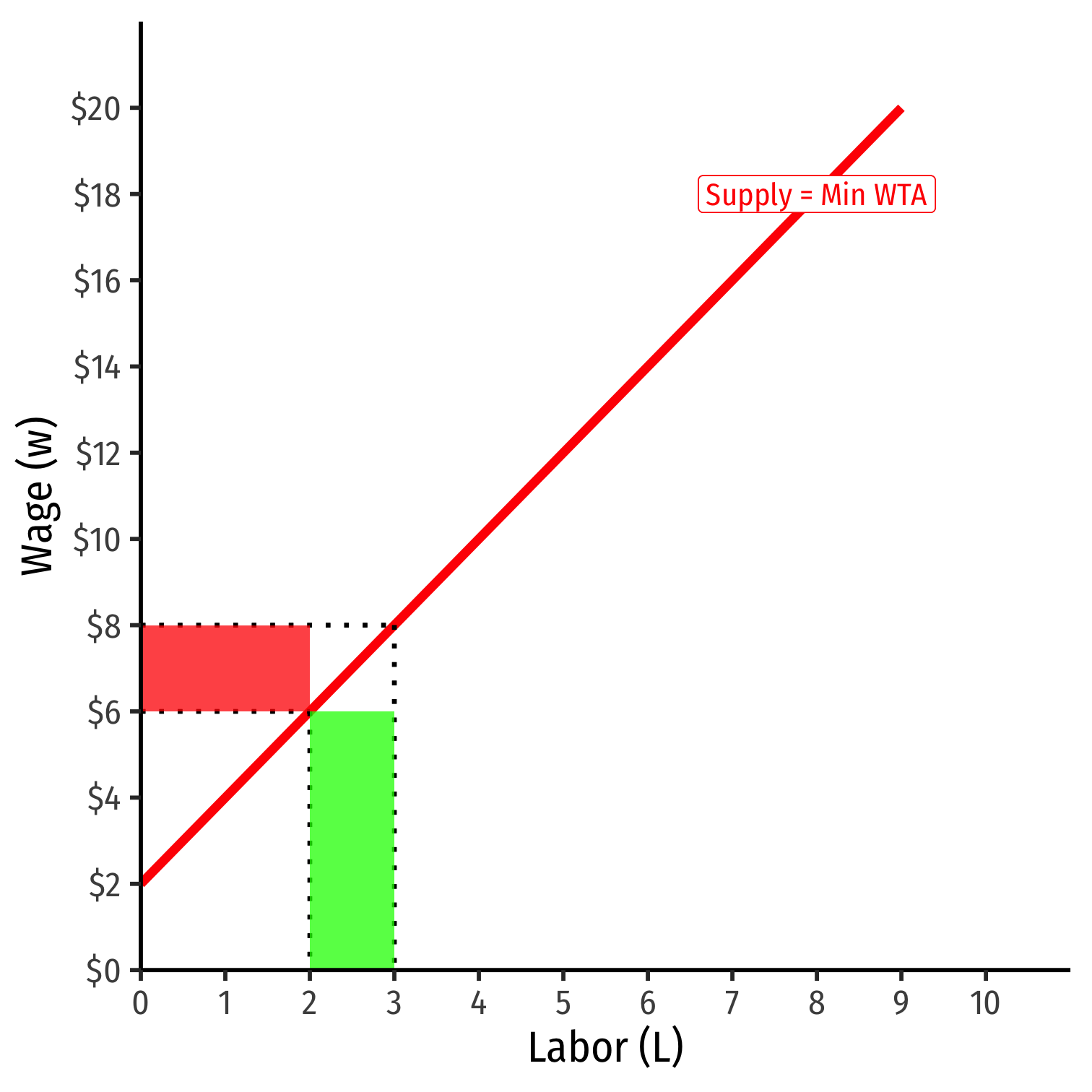
As firm chooses to hire more \(L\), must raise wages on all workers to hire them
Output effect: increased cost from increased number of workers
Price effect: increased cost from raising wage for all workers
Monopsony and Marginal Cost of Labor I
- If monopsonist wants to hire more labor, \(\Delta L\), its labor cost \(C(L)\) would change by:
\(\Delta C(L)=\)\(w \Delta L\) \(+\) \(L \Delta w\)
Monopsony and Marginal Cost of Labor I
- If monopsonist wants to hire more labor, \(\Delta L\), its labor cost \(C(L)\) would change by:
\(\Delta C(L)=\)\(w \Delta L\) \(+\) \(L \Delta w\)
- Output effect: increases number of labor hired \((\Delta L)\) times wage \(w\) per worker
Monopsony and Marginal Cost of Labor I
- If monopsonist wants to hire more labor, \(\Delta L\), its labor cost \(C(L)\) would change by:
\(\Delta C(L)=\)\(w \Delta L\) \(+\) \(L \Delta w\)
Output effect: increases number of labor hired \((\Delta L)\) times wage \(w\) per worker
Price effect: raises wage per worker \((\Delta w)\) on all workers hired \((L)\)
Monopsony and Marginal Cost of Labor I
- If monopsonist wants to hire more labor, \(\Delta L\), its labor cost \(C(L)\) would change by:
\(\Delta C(L)=\)\(w \Delta L\) \(+\) \(L \Delta w\)
Output effect: increases number of labor hired \((\Delta L)\) times wage \(w\) per worker
Price effect: raises wage per worker \((\Delta w)\) on all workers hired \((L)\)
Divide both sides by \(\Delta L\) to get Marginal Cost of Labor, \(MC(L)\):
$$\frac{\Delta C(L)}{\Delta L}=\color{#6A5ACD}{MC(L)=w+\frac{\Delta w}{\Delta L}L}$$
Monopsony and Marginal Cost of Labor I
- If monopsonist wants to hire more labor, \(\Delta L\), its labor cost \(C(L)\) would change by:
\(\Delta C(L)=\)\(w \Delta L\) \(+\) \(L \Delta w\)
Output effect: increases number of labor hired \((\Delta L)\) times wage \(w\) per worker
Price effect: raises wage per worker \((\Delta w)\) on all workers hired \((L)\)
Divide both sides by \(\Delta L\) to get Marginal Cost of Labor, \(MC(L)\):
$$\frac{\Delta C(L)}{\Delta L}=\color{#6A5ACD}{MC(L)=w+\frac{\Delta w}{\Delta L}L}$$
- Compare: supply for a price-taking firm is perfectly elastic: \(\color{#6A5ACD}{\frac{\Delta w}{\Delta L}}=0\), so we saw \(\color{#6A5ACD}{MC(L)=w}\)!
Monopsony and Marginal Cost of Labor II
- If we have a linear inverse supply function for labor of the form
$$\color{#e64173}{w=a+bL}$$
- \(a\) is the choke price (intercept)
- \(b\) is the slope
Monopsony and Marginal Cost of Labor II
- If we have a linear inverse supply function for labor of the form
$$\color{#e64173}{w=a+bL}$$
- \(a\) is the choke price (intercept)
- \(b\) is the slope
- Marginal cost of labor again is defined as: $$MC(L)=w+\color{#44C1C4}{\frac{\Delta w}{\Delta L}}L$$
Monopsony and Marginal Cost of Labor II
- If we have a linear inverse supply function for labor of the form
$$\color{#e64173}{w=a+bL}$$
- \(a\) is the choke price (intercept)
- \(b\) is the slope
- Marginal cost of labor again is defined as: $$MC(L)=w+\color{#44C1C4}{\frac{\Delta w}{\Delta L}}L$$
- Recognize that \(\color{#44C1C4}{\frac{\Delta w}{\Delta L}}\) is the slope, \(b\), \(\left(\frac{rise}{run} \right)\)
Monopsony and Marginal Cost of Labor II
- If we have a linear inverse supply function for labor of the form
$$\color{#e64173}{w=a+bL}$$
- \(a\) is the choke price (intercept)
- \(b\) is the slope
- Marginal cost of labor again is defined as: $$MC(L)=w+\color{#44C1C4}{\frac{\Delta w}{\Delta L}}L$$
- Recognize that \(\color{#44C1C4}{\frac{\Delta w}{\Delta L}}\) is the slope, \(b\), \(\left(\frac{rise}{run} \right)\)
$$\begin{align*} MC(L)&=w+(\color{#44C1C4}{b})L\\ MC(L)&=(\color{#e64173}{a+bL})+bL\\ \color{#6A5ACD}{MC(L)}&=\color{#6A5ACD}{a+2bL}\\ \end{align*}$$
Monopsony and Marginal Cost of Labor IV
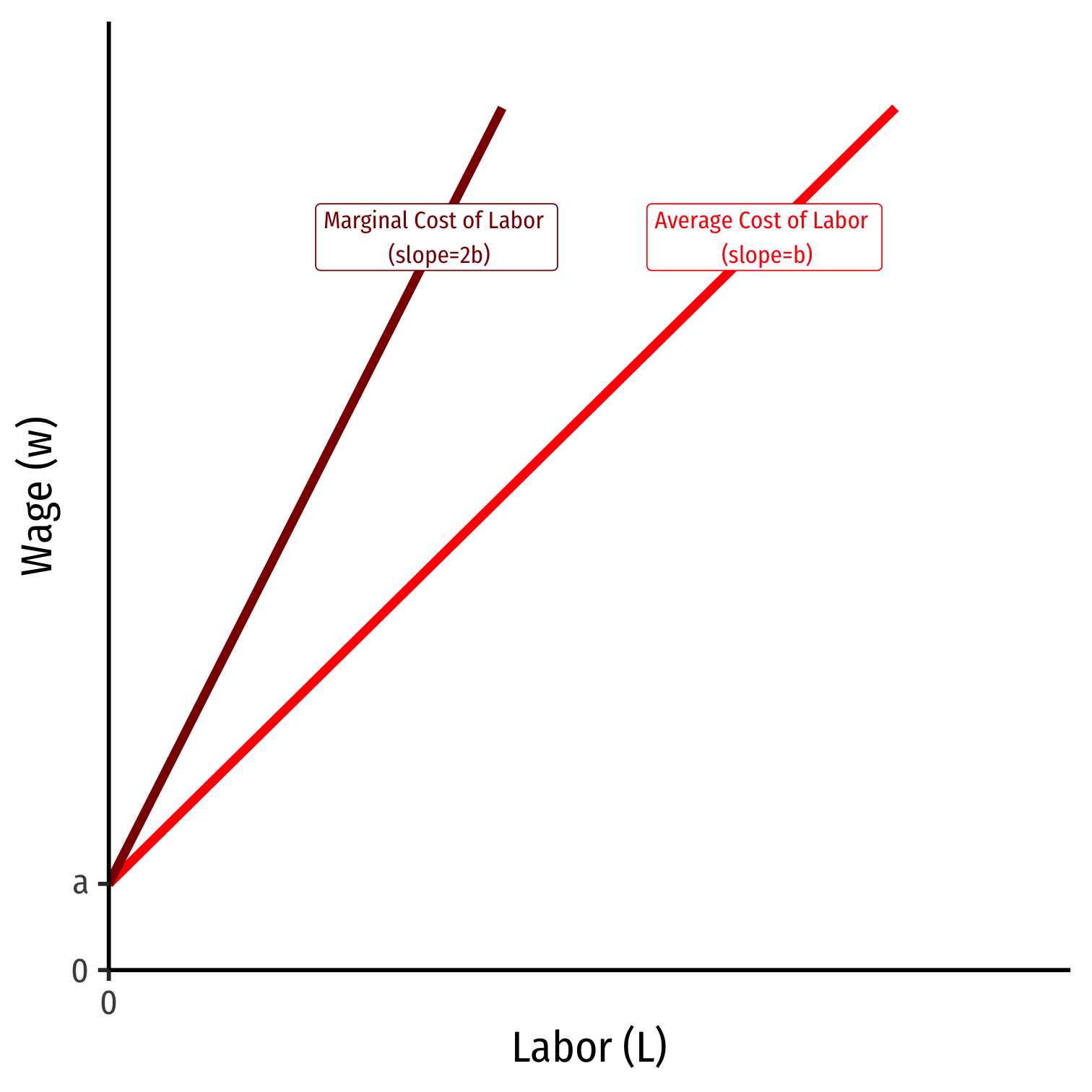
$$\begin{align*} \color{#D7250E}{w(L)}&\color{#D7250E}{=a+bL}\\ \color{#8b1a1a}{MC(L)}&\color{#8b1a1a}{=a+2bL}\\ \end{align*}$$
- Marginal cost of labor starts at same intercept as Supply (average cost of labor) \((a)\) with twice the slope \((2b)\)
Note: If these past few slides have sounded familiar, this is the exact same process by which we derived a monopolist’s marginal revenue curve!
Monopsony's Hiring Decisions
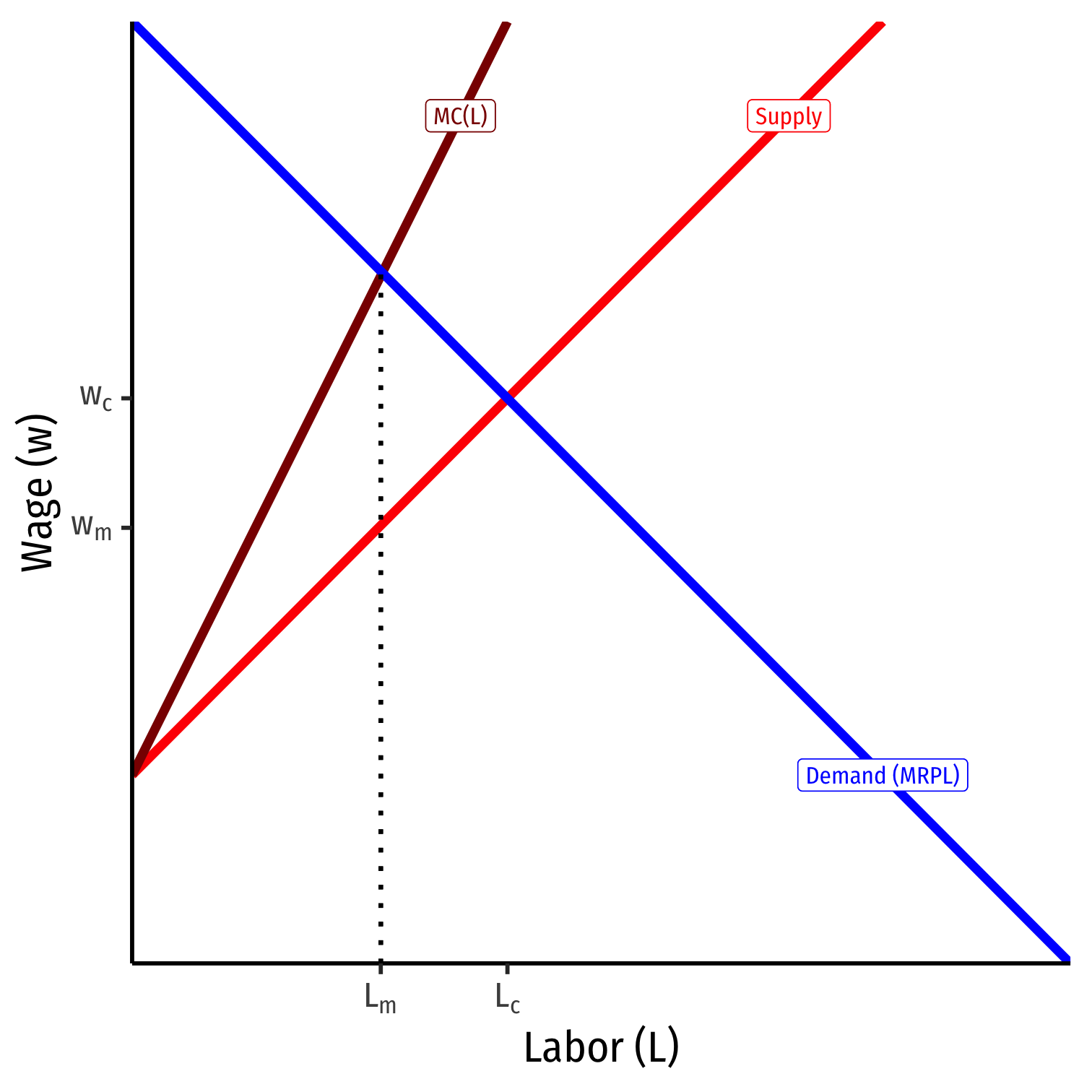
- Optimal quantity is where \(MC=MR\)
- Firm's \(MC(L)=MRP_L\)
Monopsony's Hiring Decisions
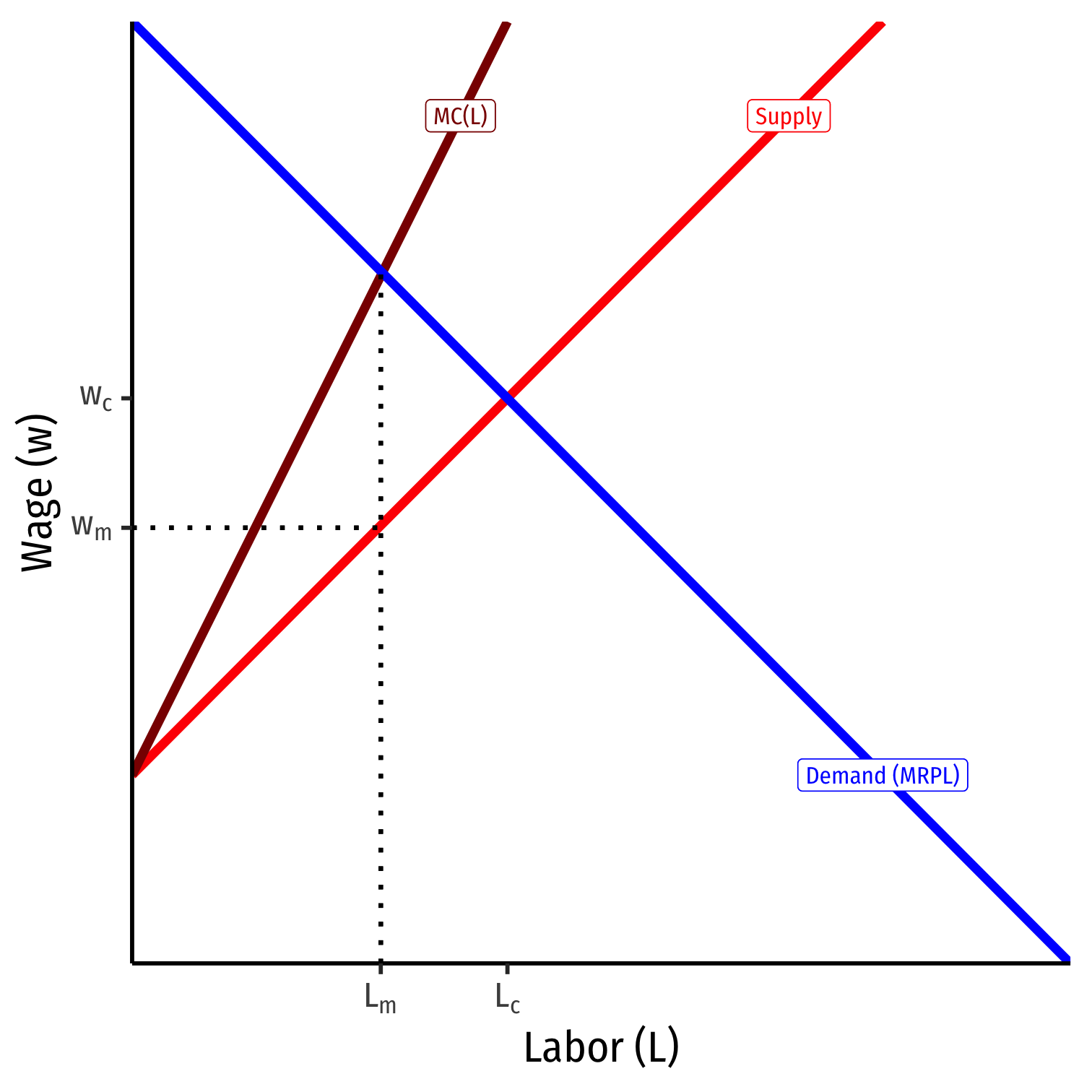
Optimal quantity is where \(MC=MR\)
- Firm's \(MC(L)=MRP_L\)
Monopsonist faces entire market supply
- Can lower wages as low as workers’ minimum WTA (Supply)
Monopsonist’s Hiring Decisions
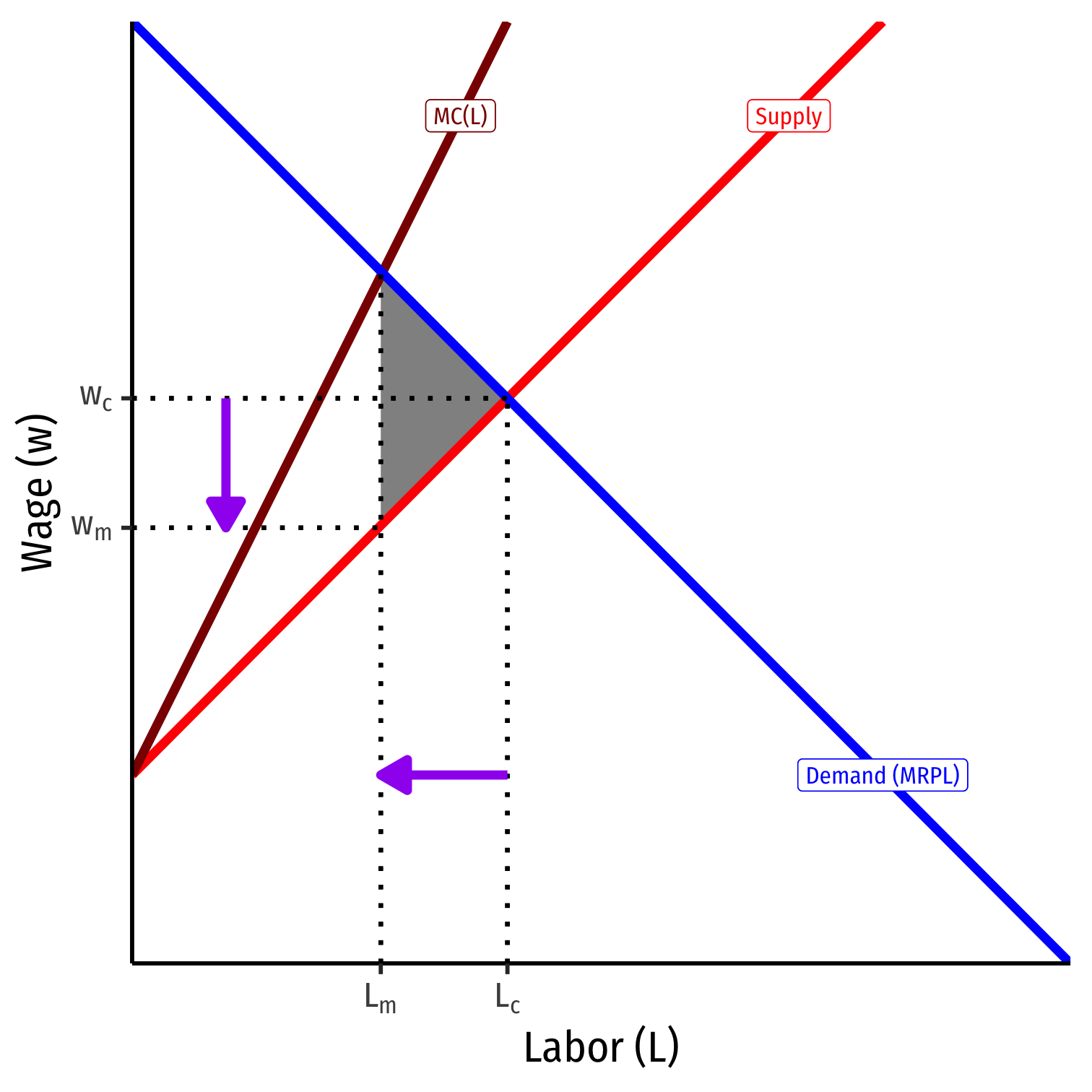
Optimal quantity is where \(MC=MR\)
- Firm's \(MC(L)=MRP_L\)
Monopsonist faces entire market supply
- Can lower wages as low as workers' minimum WTA (Supply)
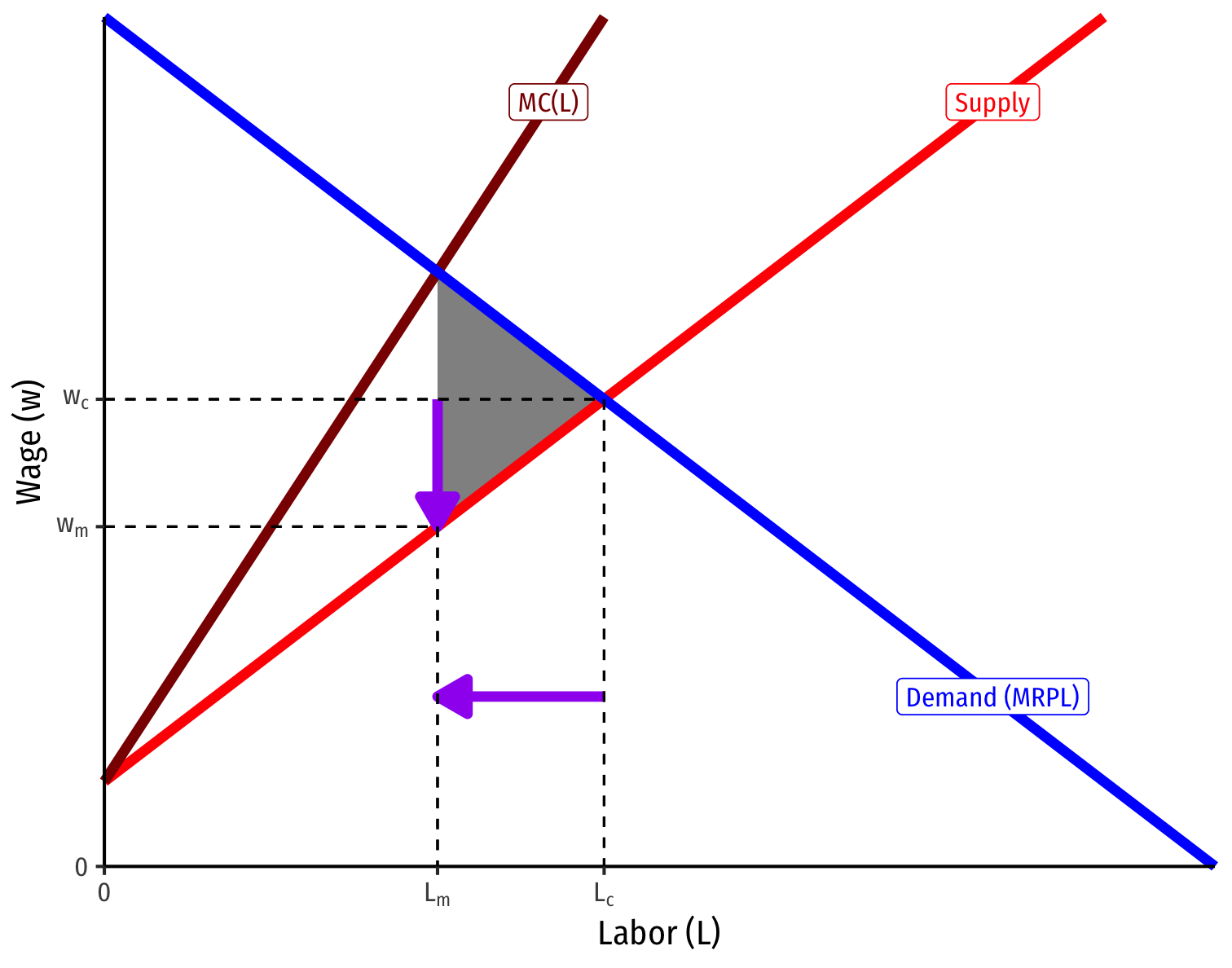
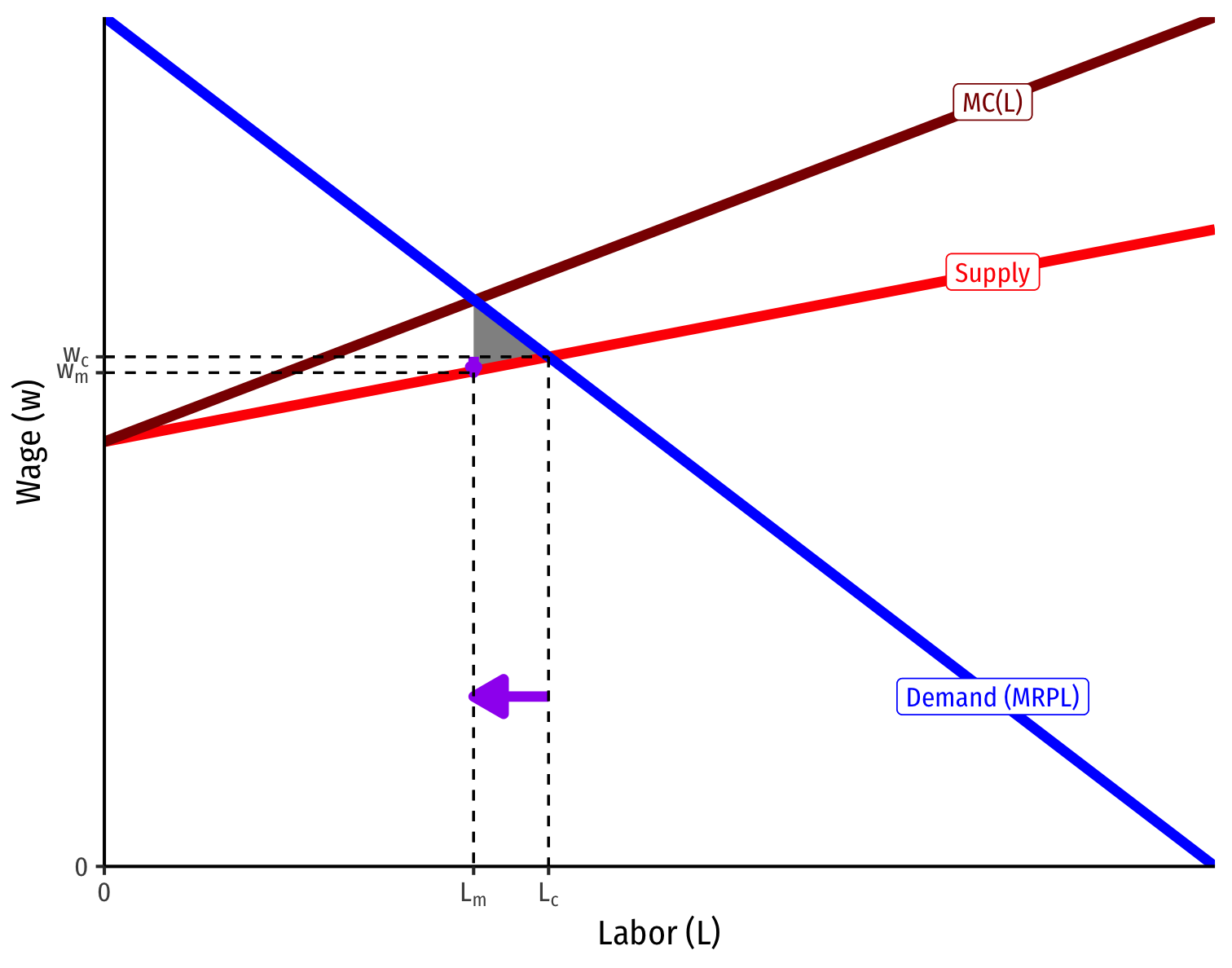
Compared to a competitive labor market \((L_c,w_c)\), monopsonist hires fewer workers and pays them lower wages \((L_m,w_m)\); creates deadweight loss
Monopsony Example II
Example: Now suppose that Victoria’s Tours is the only travel company that offers guided tours in the broader region. Its marginal revenue product of labor over the whole region, is given by $$MRP_L = 1,000 – 4L$$
where \(L\) is the number of tour-guide weeks it hires and \(MRP_L\) is measured in dollars per tour-guide week.
The market (inverse) supply of local tour guide labor is equal to $$w=200+4L$$
If this market were competitive, what would the equilibrium number of workers and the market wage be?
As a monopsonist, how many workers will Victoria's Tours hire, and what will they pay them?
Monopsony Example II
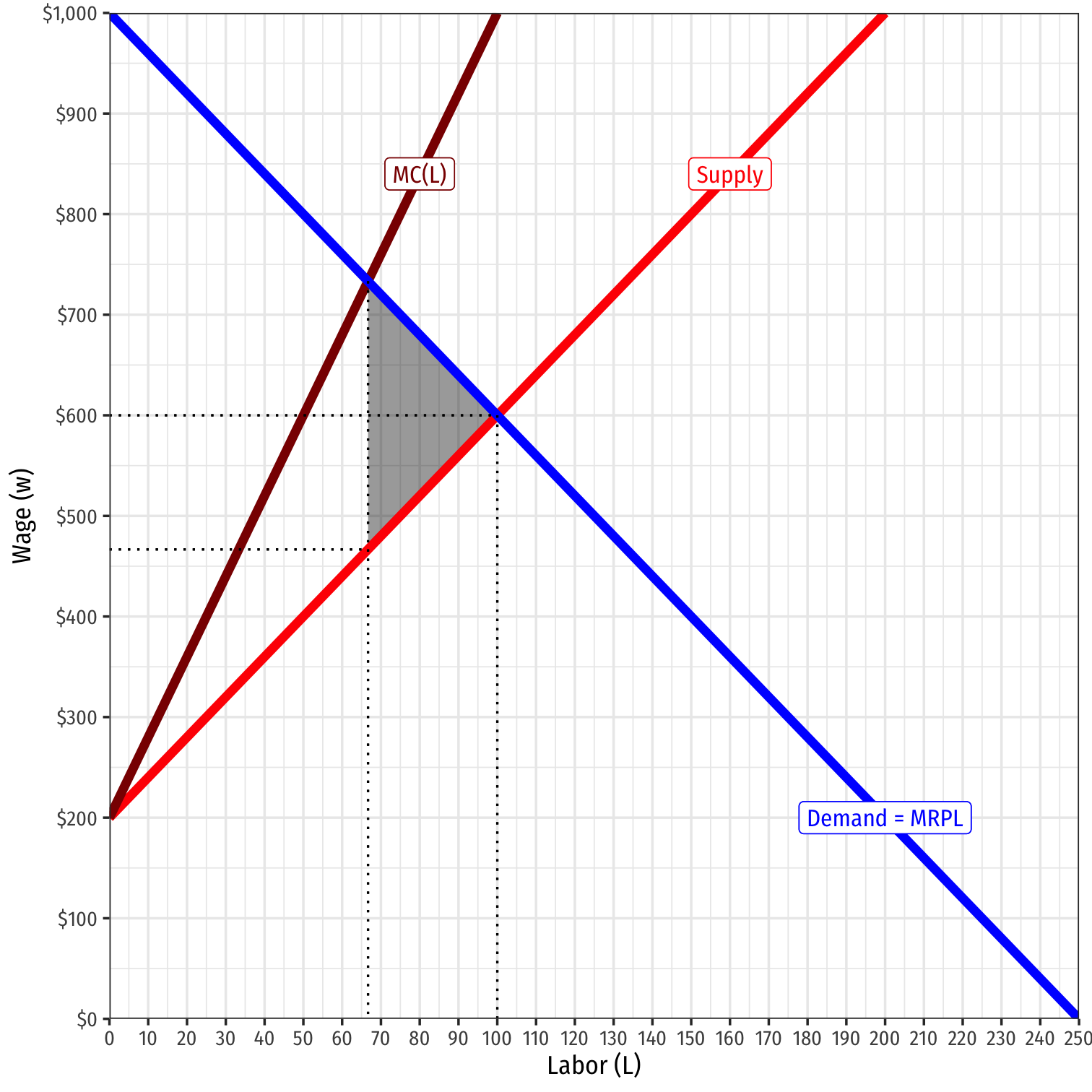
Monopsony Power Depends on Price Elasticity
The more (less) elastic labor supply, the less (more) monopsony power (and DWL)
Less Elastic Labor Supply Curve
More Elastic Labor Supply Curve
Monopoly Power in Labor Markets: Unions
Monopoly Power in Labor Markets: Unions
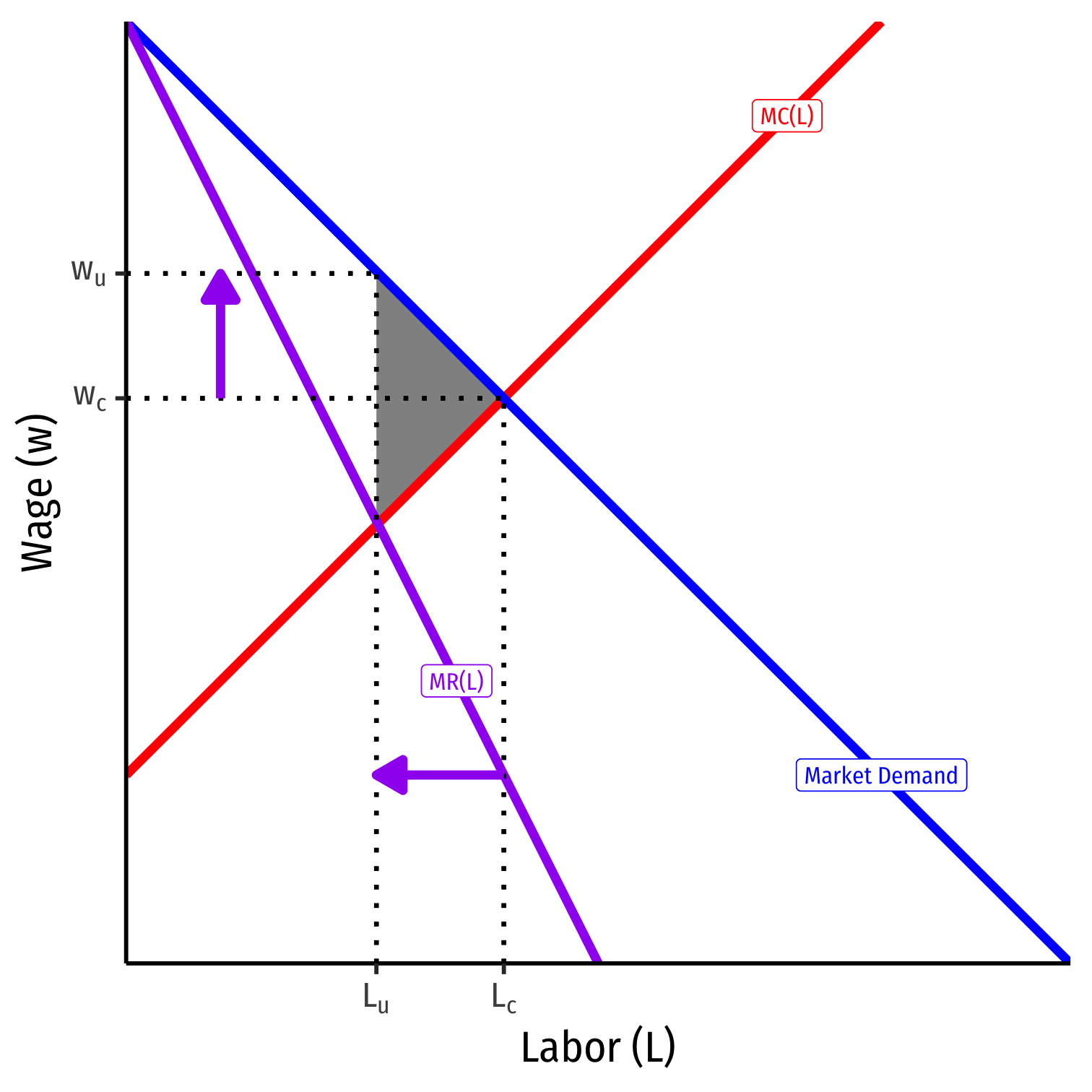
If seller/s of labor (workers) has market power, can act like a monopolist on the labor market
Example: A labor union
Faces entire market demand for labor, and thus its marginal revenue curve too
Acts like a monopolist, restricts \(L_u < L_c\) to push up \(w_u > w_c\)
The Problem of Bilateral Monopoly
What if both sides of the market have market power?
- A downstream monopsonist buyer vs. an upstream monopolist seller
This is the problem of bilateral monopoly
- We’ll examine later this semester
- One solution is vertical integration: merge into a single firm across both markets