Processing math: 33%
+ - 0:00:00
Notes for current slide
Notes for next slide

2.3 — Bertrand Competition

ECON 326 • Industrial Organization • Spring 2023

Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/ioS23
ioS23.classes.ryansafner.com

Bertrand Competition: Moblab

Bertrand Competition: Moblab

  • Each of you selling identical Economics course notes

  • You will be put into a market with one other player

  • Each term, both of you simultaneously choose your price

  • Firm(s) choosing the lowest price get all the customers

Bertrand Competition: Moblab

  • The lowest price pL determines the market demand q=3600−200pL

  • Both firms have $2 cost per unit sold

  • p=10 maximizes total market profits

Bertrand Competition: Moblab

q=3600−200pL

Example:

  • Suppose Firm 1 sets $p=\$9$ and Firm 2 sets $p=\$10$

  • Firm 2 sells 0, makes $0

  • Firm 1 sells $q=3,600-200(\$9)=1,800$ and earns $1,800(\$9-\$2)=\$12,600$ profit

Bertrand Competition

Joseph Bertrand

1822-1890

“Such is the study made in chapter VII of the rivalry between two proprietors, who without having to worry about any competition, manage two springs of identical quality. It would be in their mutual interest to associate [collude] or at least to set a common price so as to make the largest possible revenue from all the buyers, but this solution is rejected. Cournot assumes that one of the proprietors will reduce his prices to attract buyers to him and that the other will, in turn, reduce his prices even more to attract business back to him. They will only stop undercutting each other in this way when either proprietor, even if the other abandoned the struggle, has nothing more to gain from reducing his prices. One major objection to this is that there is no solution under this assumption, in that there is no limit in the downward movement. Indeed, whatever the common price adopted, if one of the proprietors, alone, reduces his price he will, ignoring any minor exceptions, attract all the buyers and thus double his revenue if his rival lets him do so. If Cournot’s formulation conceals this obvious result, it is because he most inadvertently introduces as D [q1] and D′ [q2] the two proprietors’ respective outputs and by considering them as independent variables he assumes that should either proprietor change his output then the other proprietor’s output could remain constant. It quite obviously could not,” (503).

Bertrand, Joseph, 1883, “Book review of theorie mathematique de la richesse sociale and of recherches sur les principles mathematiques de la theorie des richesses”, Journal de Savants 67: 499–508

Bertrand Competition

Joseph Bertrand

1822-1890

  • "Bertrand competition": two (or more) firms compete on price to sell identical goods

  • Firms set their prices simultaneously

  • Consumers are indifferent between the brands and always buy from the seller with the lowest price

Bertrand Competition: Example

  • Consider Coke and Pepsi again, with a constant marginal cost of $0.50

  • Denote Coke's price as pc and Pepsi's price as pp

  • Let each firm’s sales Q qc and qp be determined by the price each chose, QD(pc) and QD(pp)

Bertrand Competition: Example

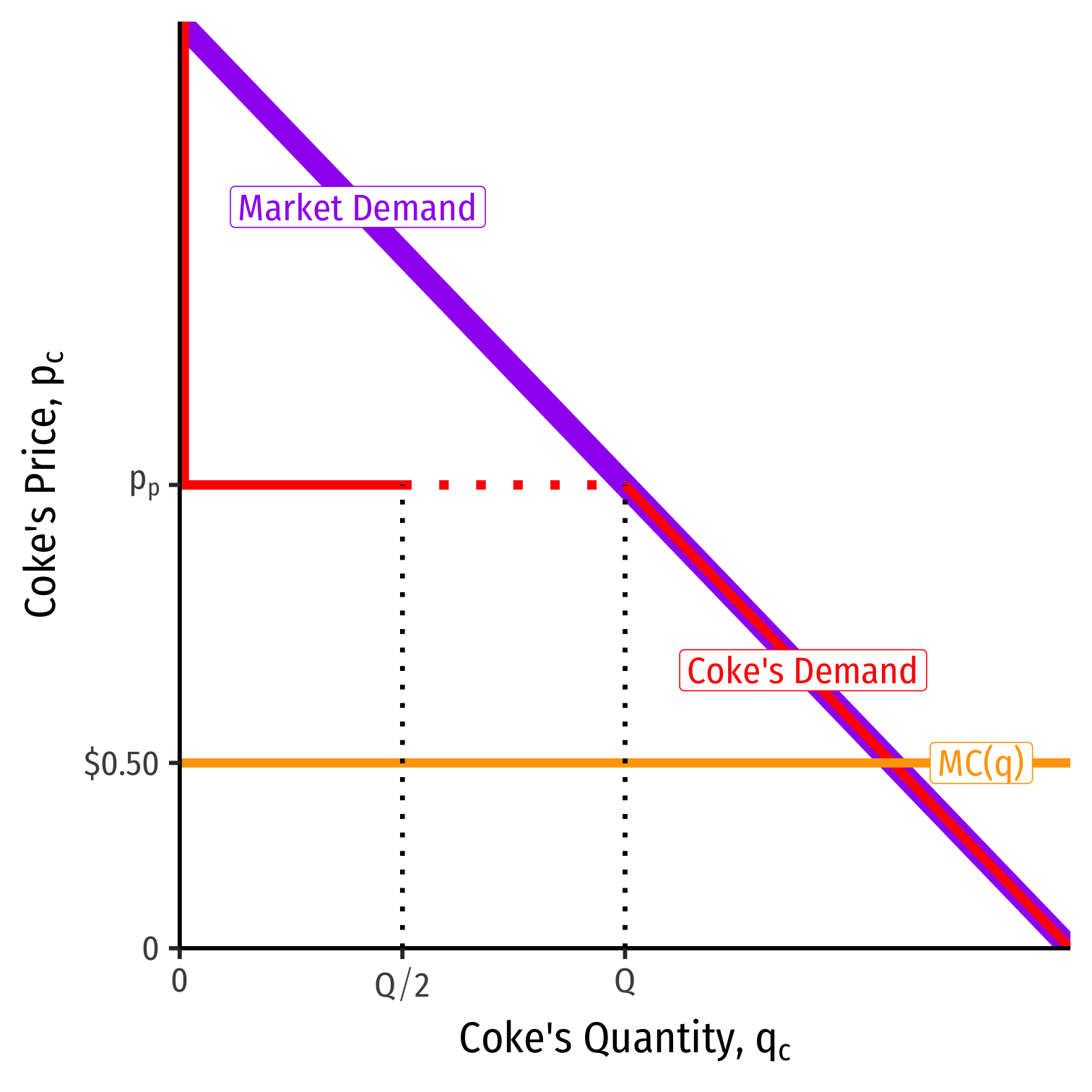
  • Demand for soda from Coke:

Bertrand Competition: Example

  • Demand for soda from Coke:
    • Q if pc < pp

Bertrand Competition: Example

  • Demand for soda from Coke:
    • Q if pc < pp
    • Q2 if pc = pp

Bertrand Competition: Example

  • Demand for soda from Coke:
    • Q if pc < pp
    • Q2 if pc = pp
    • 0 if pc > pp

Bertrand Competition: Example

  • Demand for soda from Coke:
    • Q if pc < pp
    • Q2 if pc = pp
    • 0 if pc > pp

Bertrand Competition: Example

  • Demand for soda from Coke:
    • Q if pc < pp
    • Q2 if pc = pp
    • 0 if pc > pp
  • Demand for soda from Pepsi:
    • 0 if pc < pp
    • Q2 if pc = pp
    • Q if pc > pp

Bertrand Competition: Example

  • The only way to sell any soda is to match or beat your competitor's price

Bertrand Competition: Example

  • The only way to sell any soda is to match or beat your competitor's price

  • Suppose you are Coke

  • For a given pp, setting your price pc=pp−ϵ for any arbitrary ϵ>0 captures you the entire market Q

  • Same for Pepsi for pc

Bertrand Competition: Example

  • Won't charge p<MC, earn losses

  • Firms continue undercutting one another until pc = pp =MC

    • No incentive for either firm to raise or lower price, given other firm‘s price

  • Nash Equilibrium: (pc=MC,pp=MC)

    • Firms earn no profits!

Bertrand Paradox

  • Bertrand Paradox: when firms compete on price, the perfectly competitive outcome can be achieved with just 2 firms!
    • p=MC
    • Q=Q(p=MC)
    • π=0
    • L=p−MCp=0!

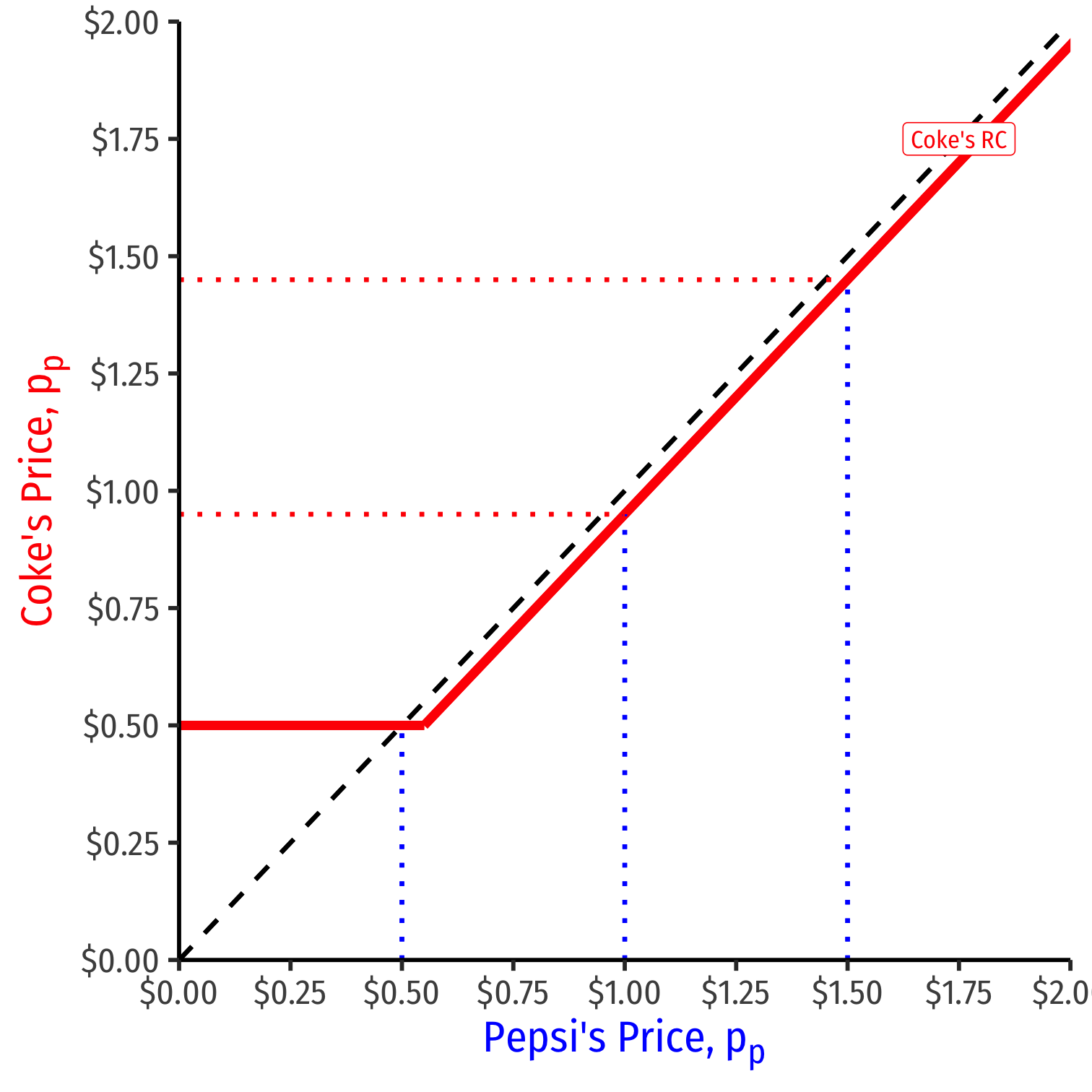
Coke's Reaction Curve

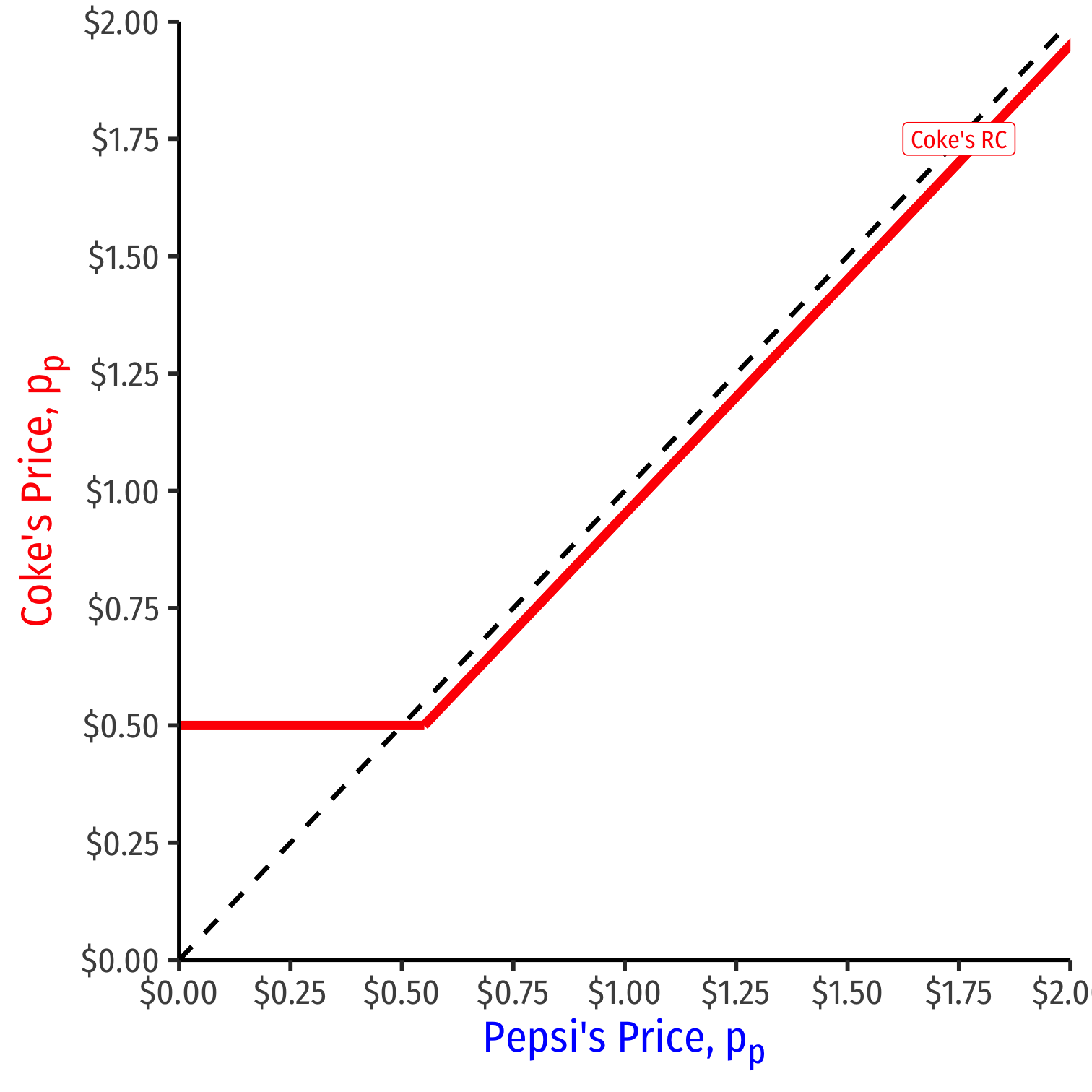
We can graph Coke's reaction curve to Pepsi's price

Coke's Reaction Curve

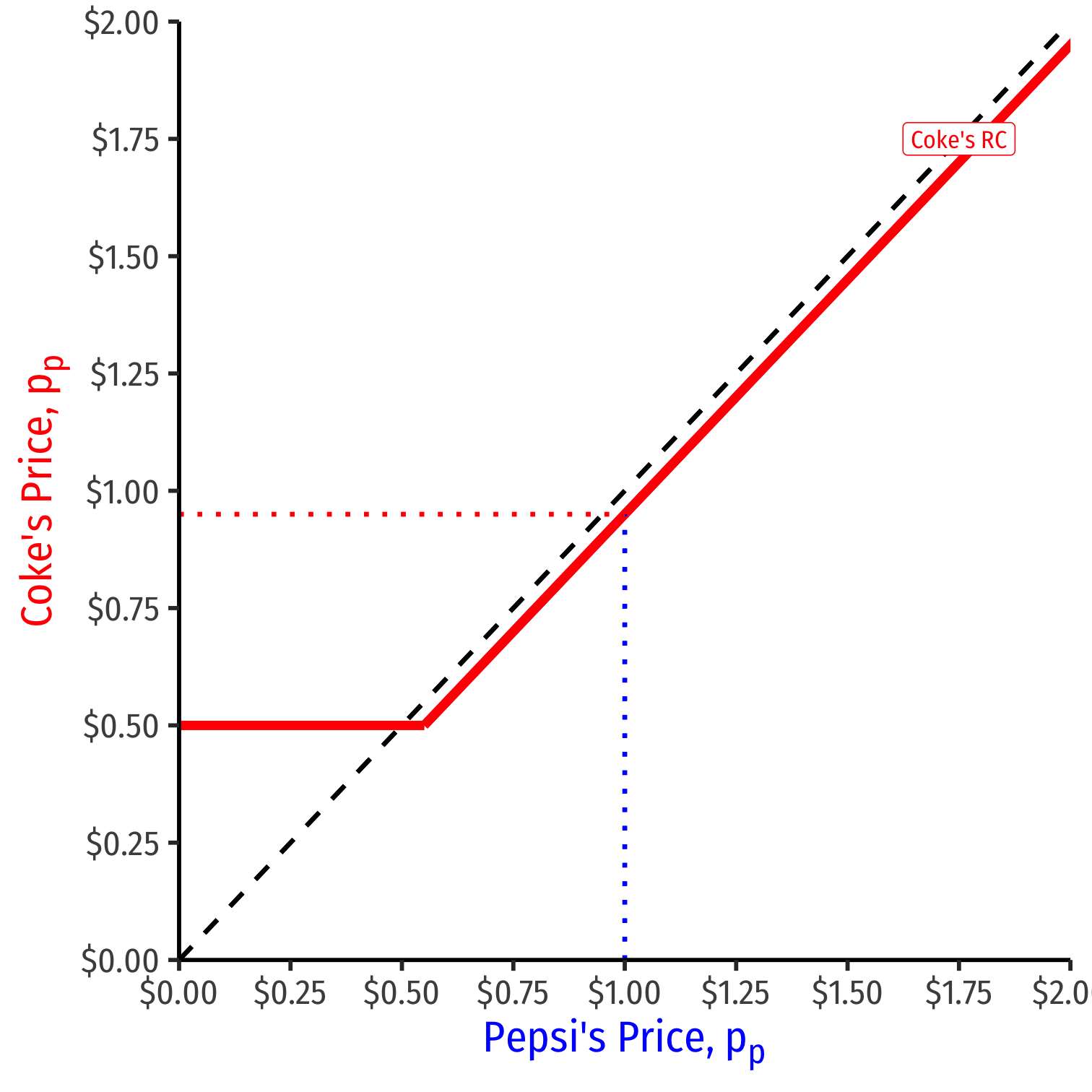
We can graph Coke's reaction curve to Pepsi's price

pc={pp−ϵif pp>cppif pp=c

  • e.g. if Pepsi sets a price of $1.00, Coke's best response is $1.00−ϵ

Coke's Reaction Curve

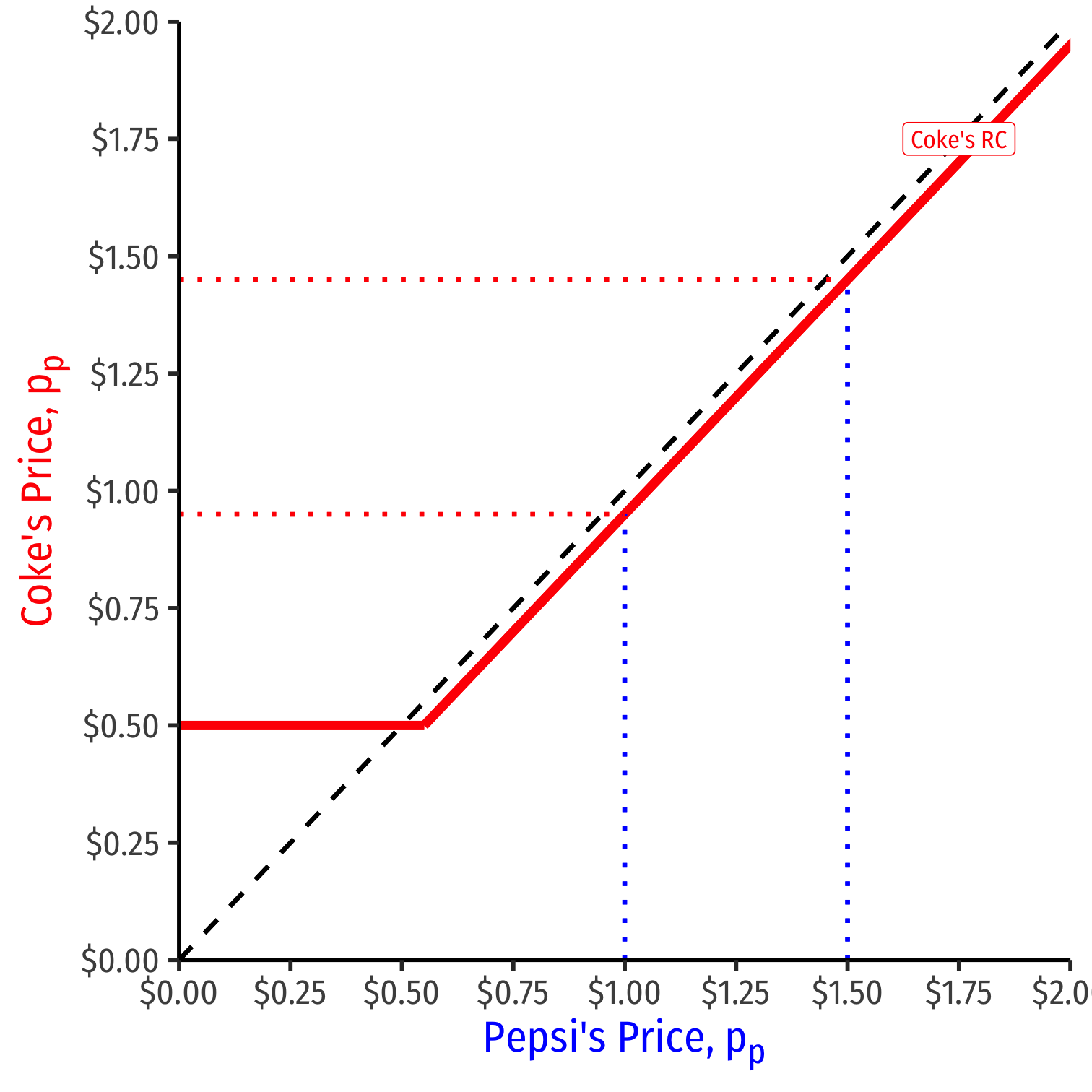
We can graph Coke's reaction curve to Pepsi's price pc={pp−ϵif pp>cppif pp=c

  • e.g. if Pepsi sets a price of $1.50, Coke's best response is $1.50−ϵ
  • e.g. if Pepsi sets a price of $1.50, Coke's best response is $1.50−ϵ

Coke's Reaction Curve

We can graph Coke's reaction curve to Pepsi's price pc={pp−ϵif pp>cppif pp=c

  • e.g. if Pepsi sets a price of $1.50, Coke's best response is $1.50−ϵ
  • e.g. if Pepsi sets a price of $1.50, Coke's best response is $1.50−ϵ
  • e.g. if Pepsi sets a price of $0.50, (MC) Coke's best response is $0.50 (MC)

Pepsi's Reaction Curve

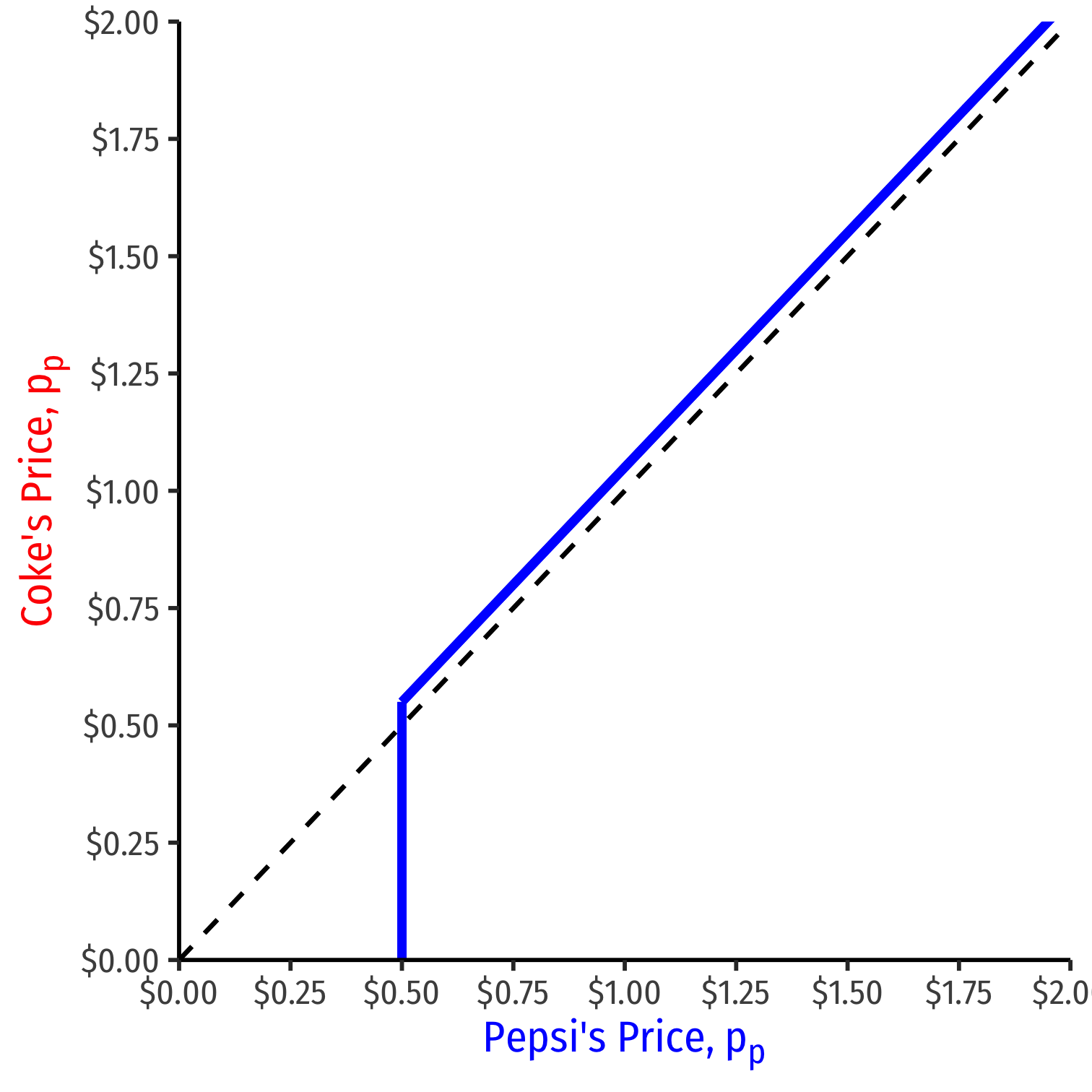
We can graph Pepsi's reaction curve to Coke's price

Pepsi's Reaction Curve

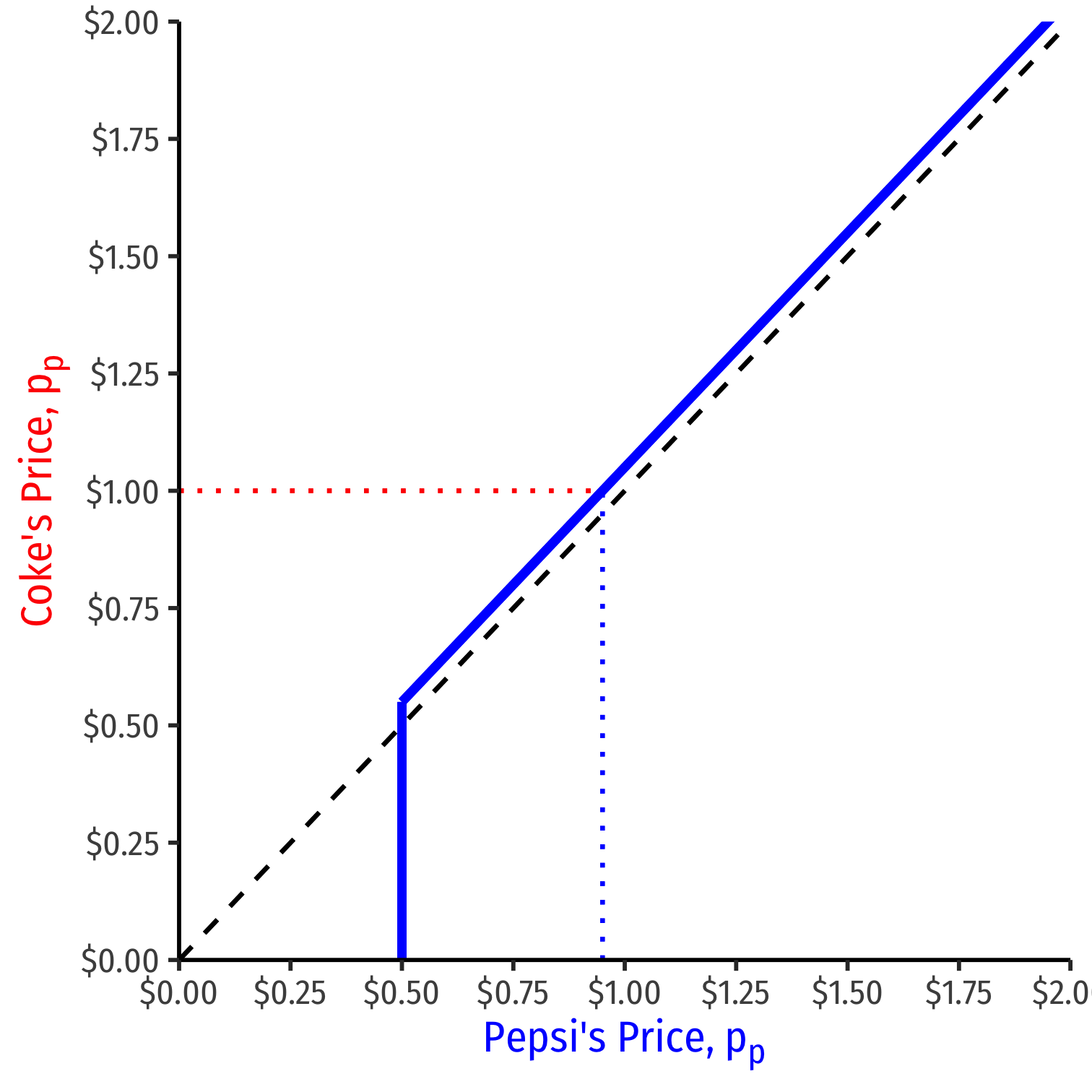
We can graph Pepsi's reaction curve to Coke's price pp={pc−ϵif pc>cpxif pc=c

  • e.g. if Coke sets a price of $1.00, Pepsi's best response is $1.00−ϵ

Pepsi's Reaction Curve

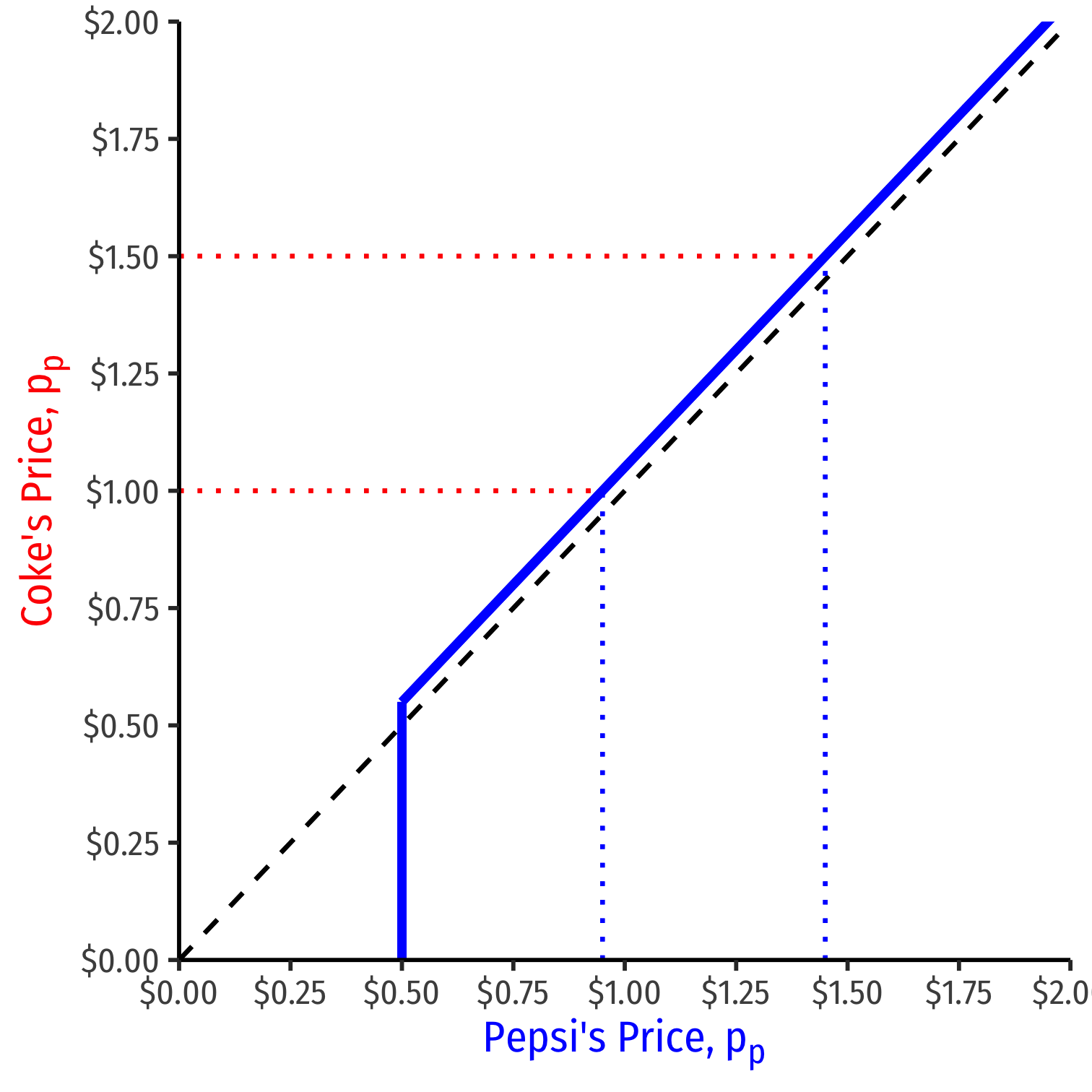
We can graph Pepsi's reaction curve to Coke's price pp={pc−ϵif pc>cpxif pc=c

  • e.g. if Coke sets a price of $1.00, Pepsi's best response is $1.00−ϵ
  • e.g. if Coke sets a price of $1.50, Pepsi's best response is $1.50−ϵ

Pepsi's Reaction Curve

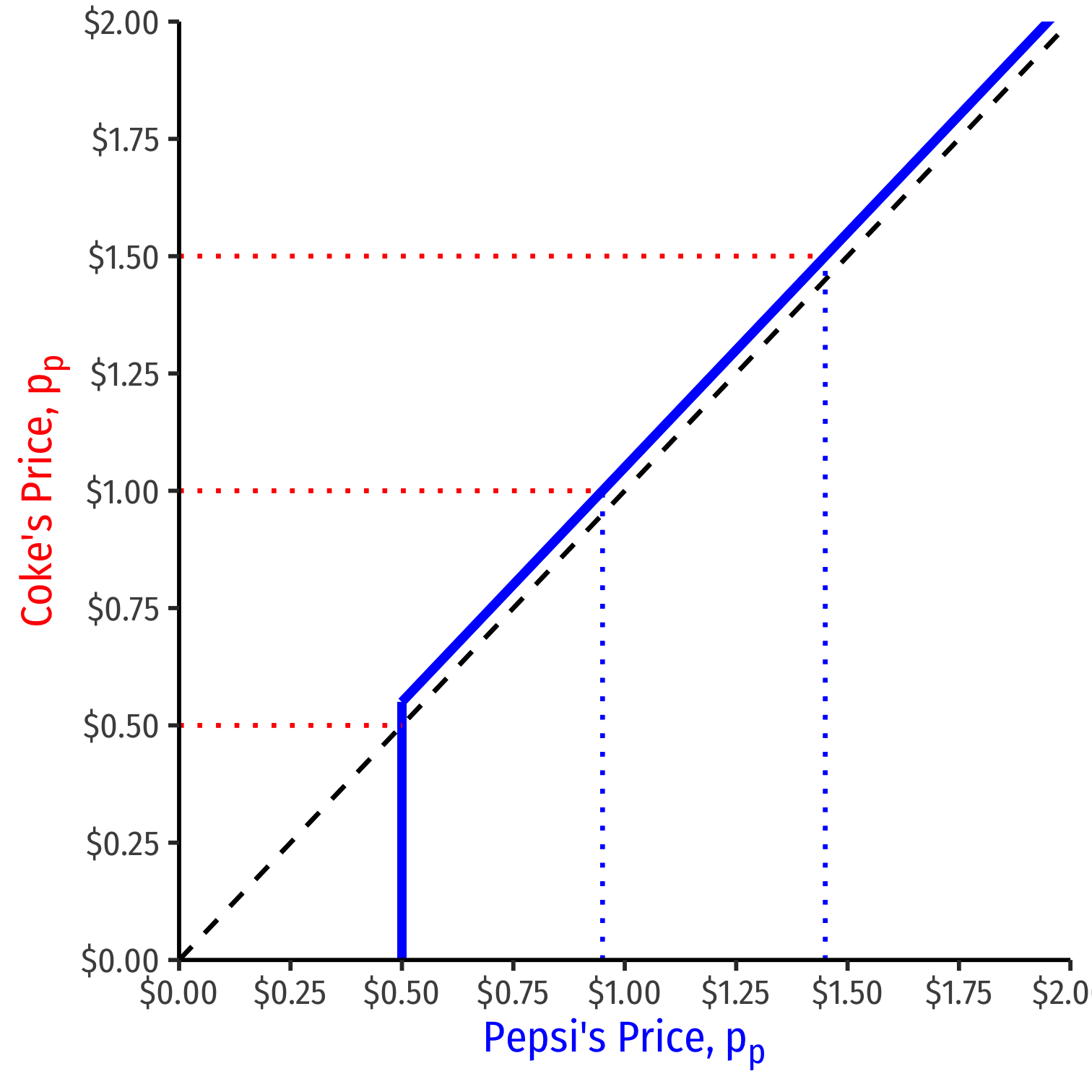
We can graph Pepsi's reaction curve to Coke's price pp={pc−ϵif pc>cpxif pc=c

  • e.g. if Coke sets a price of $1.00, Pepsi's best response is $1.00−ϵ
  • e.g. if Coke sets a price of $1.50, Pepsi's best response is $1.50−ϵ
  • e.g. if Coke sets a price of $0.50 (MC), Pepsi's best response is $0.50 (MC)

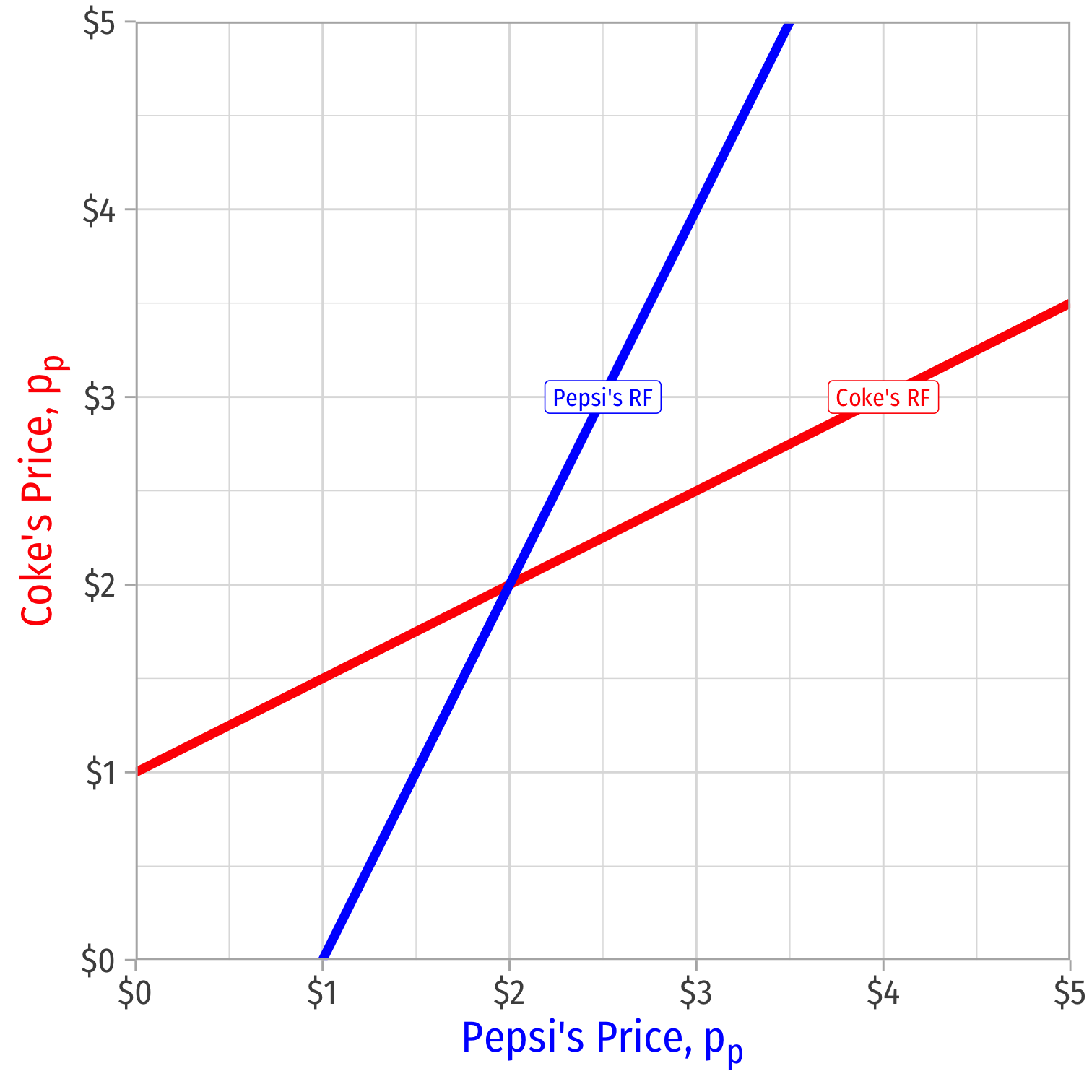
Nash Equilibrium with Reaction Curves

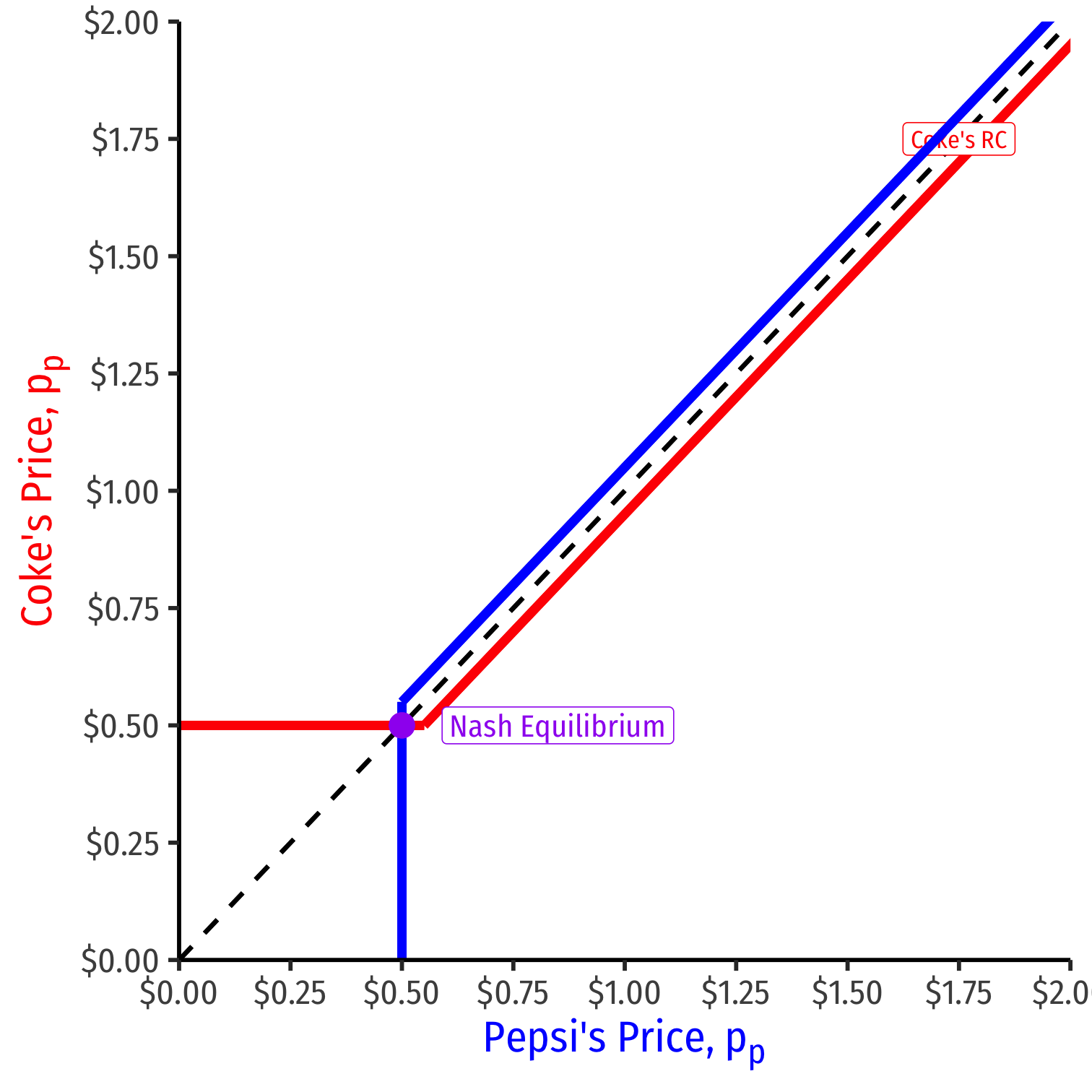
  • Combine both curves on the same graph

  • Nash Equilibrium: (pc=MC,pp=MC)

    • Where both reaction curves intersect

  • No longer an incentive to undercut or change price

Bertrand Competition: The Market

  • We can find the industry price & quantity of output (and profits), like in the Cournot model

  • Here, set p=MC

Bertrand Competition: The Market

  • We can find the industry price & quantity of output (and profits), like in the Cournot model

  • Here, set p=MC

5−0.05Q=0.50

Bertrand Competition: The Market

  • We can find the industry price & quantity of output (and profits), like in the Cournot model

  • Here, set p=MC

5−0.05Q=0.50

Q∗=90

q⋆1=q⋆2=45

Bertrand Competition: The Market

  • We can find the industry price & quantity of output (and profits), like in the Cournot model

  • Here, set p=MC

5−0.05Q=0.50

Q∗=90

q⋆1=q⋆2=45 P∗=c=$0.50

Bertrand Competition: The Market

  • We can find the industry price & quantity of output (and profits), like in the Cournot model

  • Here, set p=MC

5−0.05Q=0.50

Q∗=90

q⋆1=q⋆2=45 P∗=c=$0.50

π1=π2=Π=0

Bertrand Competition: The Market

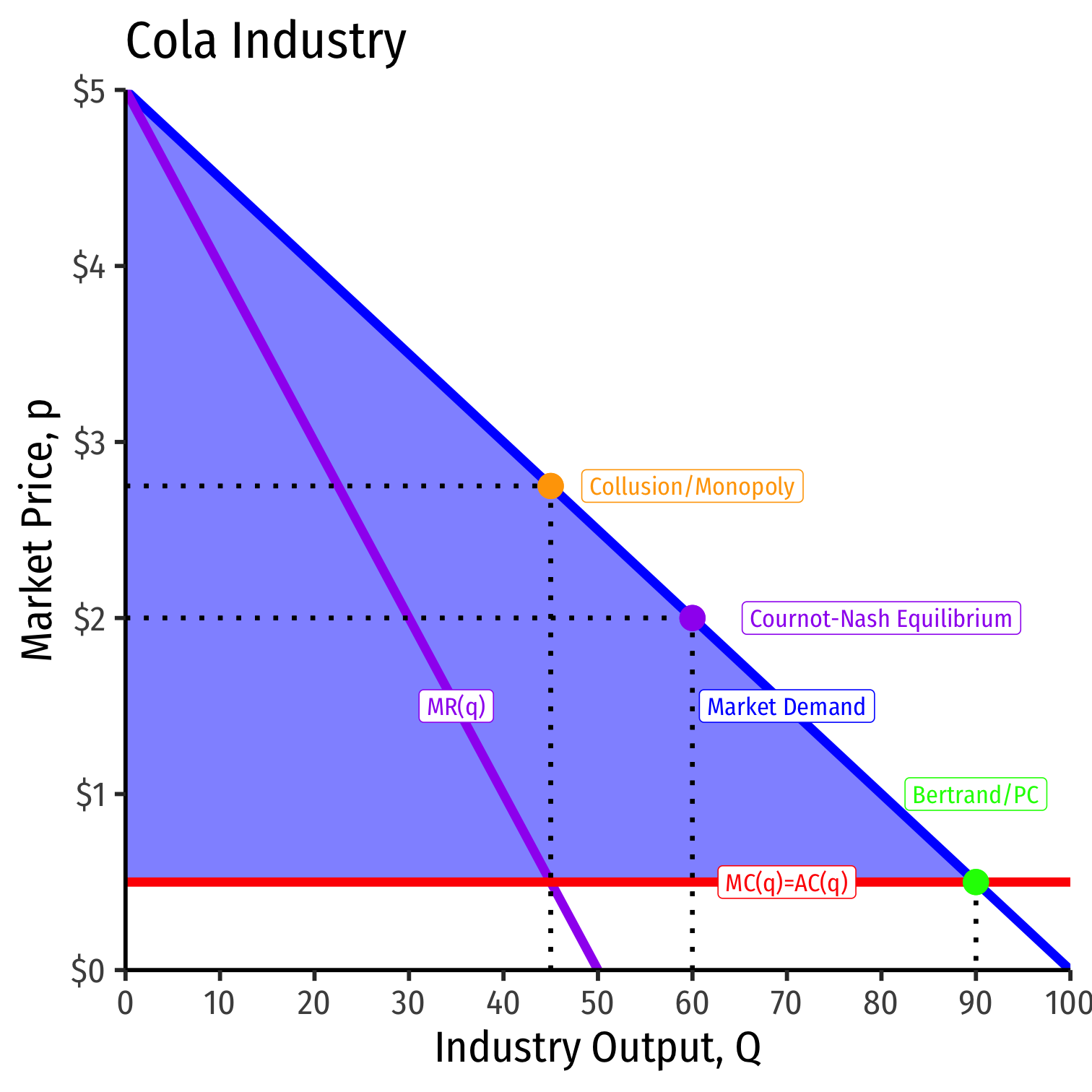
Cournot vs. Bertrand Competition

Competition qi Q p πi
Collusion 22.5 45.0 $2.75 $50.63
Cournot 30.0 60.0 $2.00 $45.00
Bertrand 45.0 90.0 $0.50 $0.00
  • Output: Qm<Qc<Qb
  • Market price: Pb=c<Pc<Pm
  • Profit: πb=0<πc<πm

Where subscripts m is monopoly (collusion), c is Cournot, b is Bertrand

Resolving the Bertrand Paradox

Joseph Bertrand

1822-1890

  • The paradox happens due to pretty strict assumptions about the model

    • No capacity constraints
    • Homogeneous goods; consumers only buy from the lower-priced seller

  • We can extend the Bertrand model in a few ways and see the paradox resolved, we'll examine two:

    1. Bertrand competition with capacity constraints
    2. Bertrand competition with differentiated products

Bertrand Competition with Capacity Constraints

Capacity Constraints

  • One way to resolve the paradox is to assume that each firm has limited capacity to produce, and cannot supply the entire market

    • certainly can't “flood” the market in a price war to drive price to MC

  • Consider in the short run we assume capital is fixed

  • Many goods/services are constrained by capacity: hotels, movie theaters, restaurants, etc.

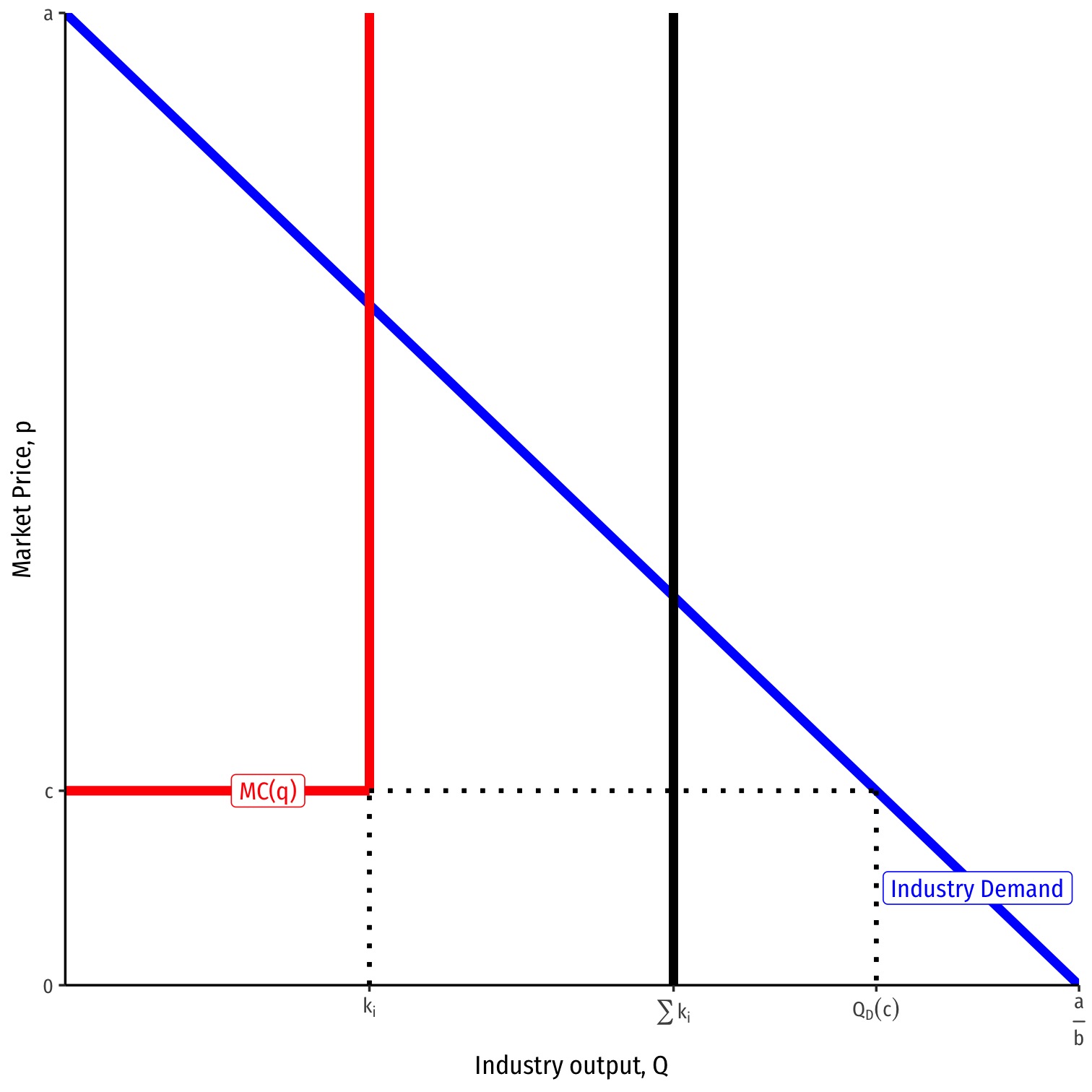
Capacity Constraints

  • Suppose each firm can only supply, at most:

q1≤k1q2≤k2k1+k2<QD(c)

  • Neither firm, nor both of them combined, can supply the entire market at marginal cost

  • Cost per unit for firm i is c up for qi<ki, then increases rapidly (if not ∞)

Capacity Constraints Change the Game

  • Suppose Pepsi charges a price pp>c.

  • Coke would simply have to charge pc=pp−ϵ to capture the market

    • But Coke does not have the capacity to serve the whole market!
    • Some customers would still buy Pepsi!
    • So Pepsi can charge a price above marginal cost

  • pc=pp=c is not a Nash equilibrium any more

Capacity Constraints

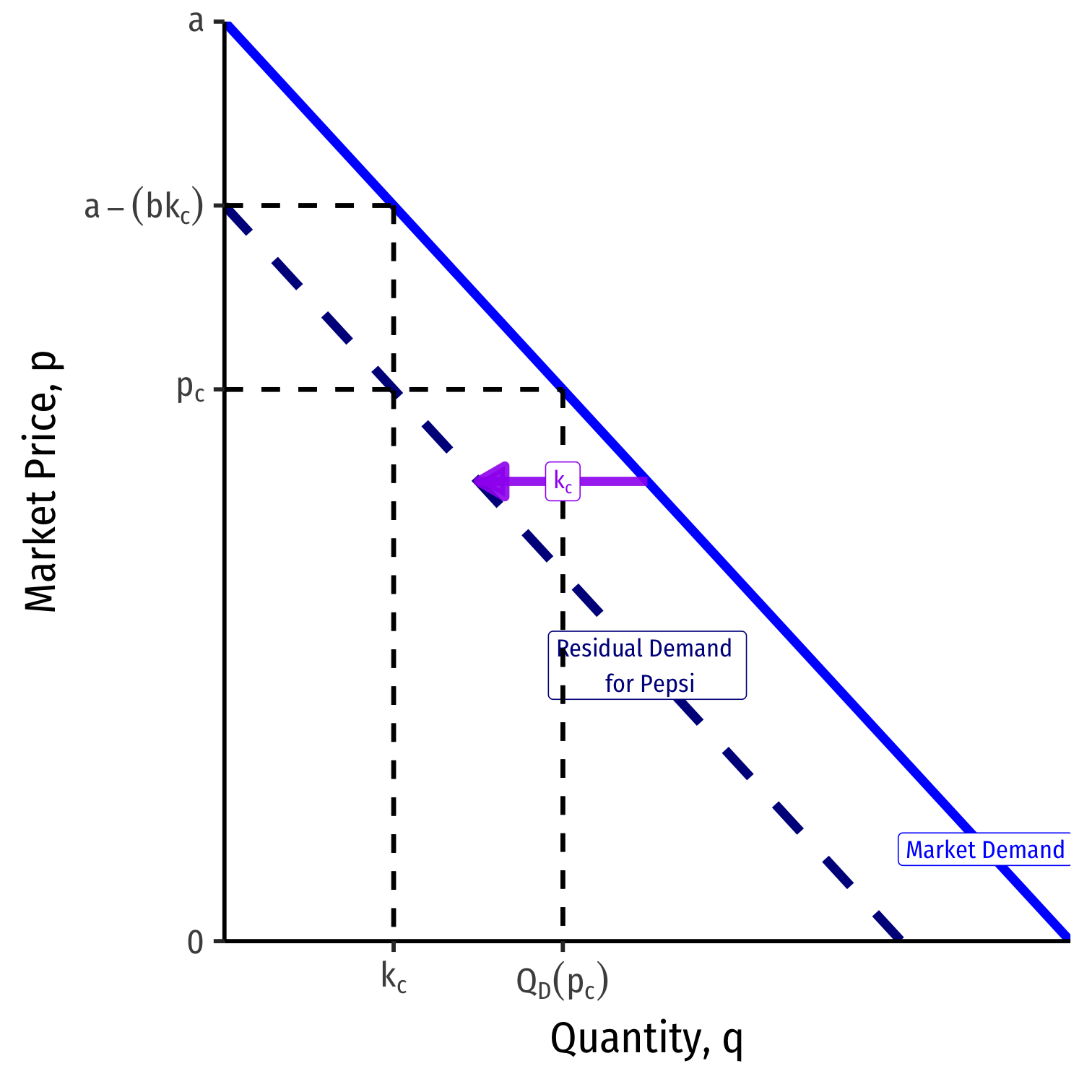
  • Suppose Coke charges a price lower than Pepsi pc<pp.

    • But Coke does not have the capacity to serve the whole market, kc<QD(pc)!
    • Some customers will still buy Pepsi!

  • Since neither firm can serve the whole market, we assume that they ration efficiently, that is, Coke only serve the customers with highest willingness to pay (first)

  • Pepsi's residual demand is thus subtracting kc from the market demand

    • Note: the same as Cournot model residual demand, assuming qc=qk, i.e. Coke sells at capacity

Capacity Constraints

  • Consider the perspective of Coke:

  • If it charges pc<pp, then it will sell min

    • Either fulfills entire market demand (if its capacity \color{red}{k_c} exceeds demand); or its capacity (if \color{red}{k_c} is less than demand)
    • Q_D is quantity demanded at that price

  • If it charges \color{red}{p_c}>\color{blue}{p_p}, then it will sell \min \left\{\color{red}{k_c}, Q_D(\color{red}{p_c})-\color{blue}{k_p} \right\}

    • Pepsi sells its full capacity; Coke meets whatever demand is left (either sells its full capacity) or the remaining demand (if less than its capacity)

  • If \color{red}{p_c}=\color{blue}{p_p} then we assume demand is allocated according to relative capacities, Coke sells \min \left\{\color{red}{k_c}, \frac{\color{red}{k_c}}{(\color{red}{k_c}+\color{blue}{k_c})D(p)}\right\}

    • e.g. if Coke has 45% of total industry capacity, it takes 45% of industry demand

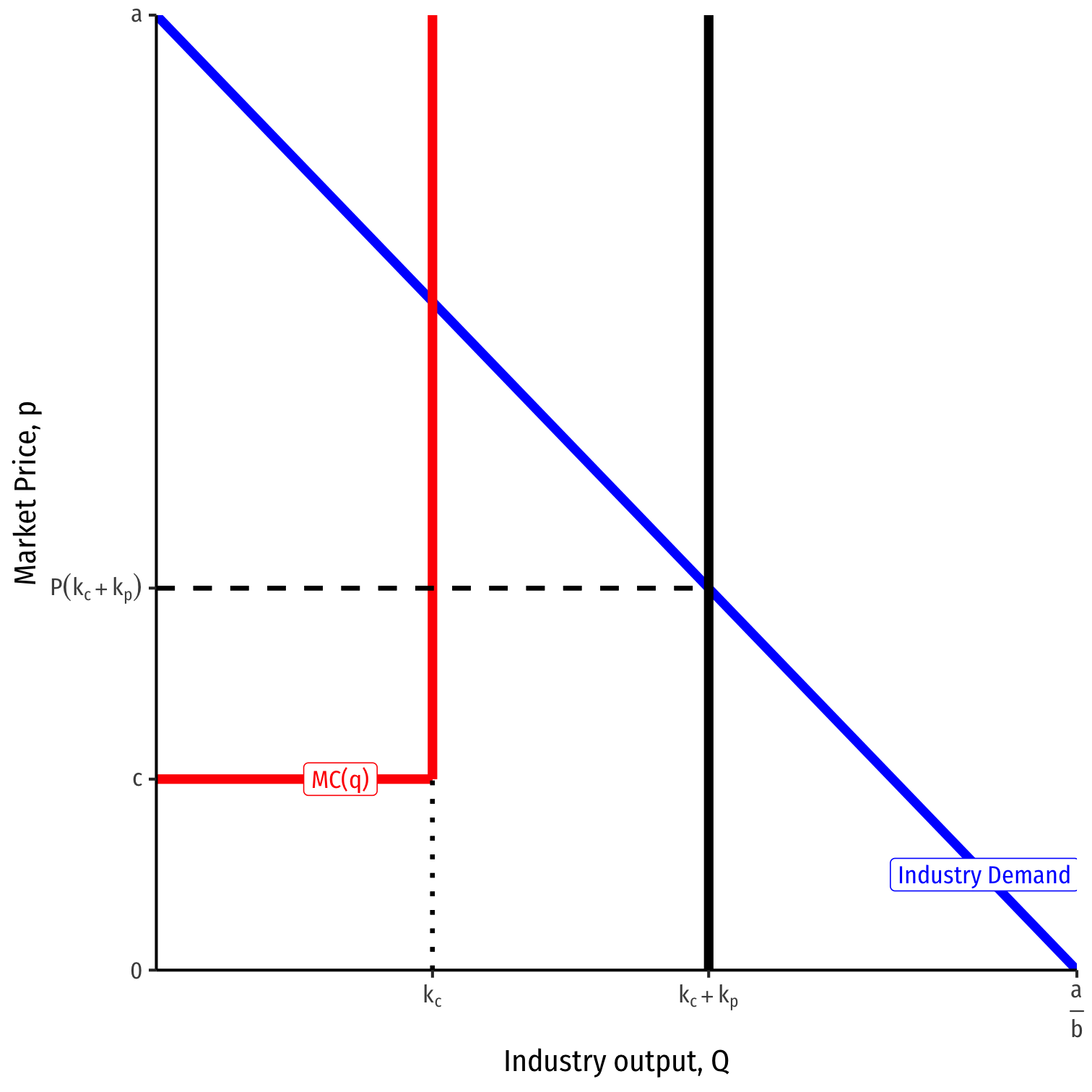
Nash Equilibrium Under Capacity Constraints

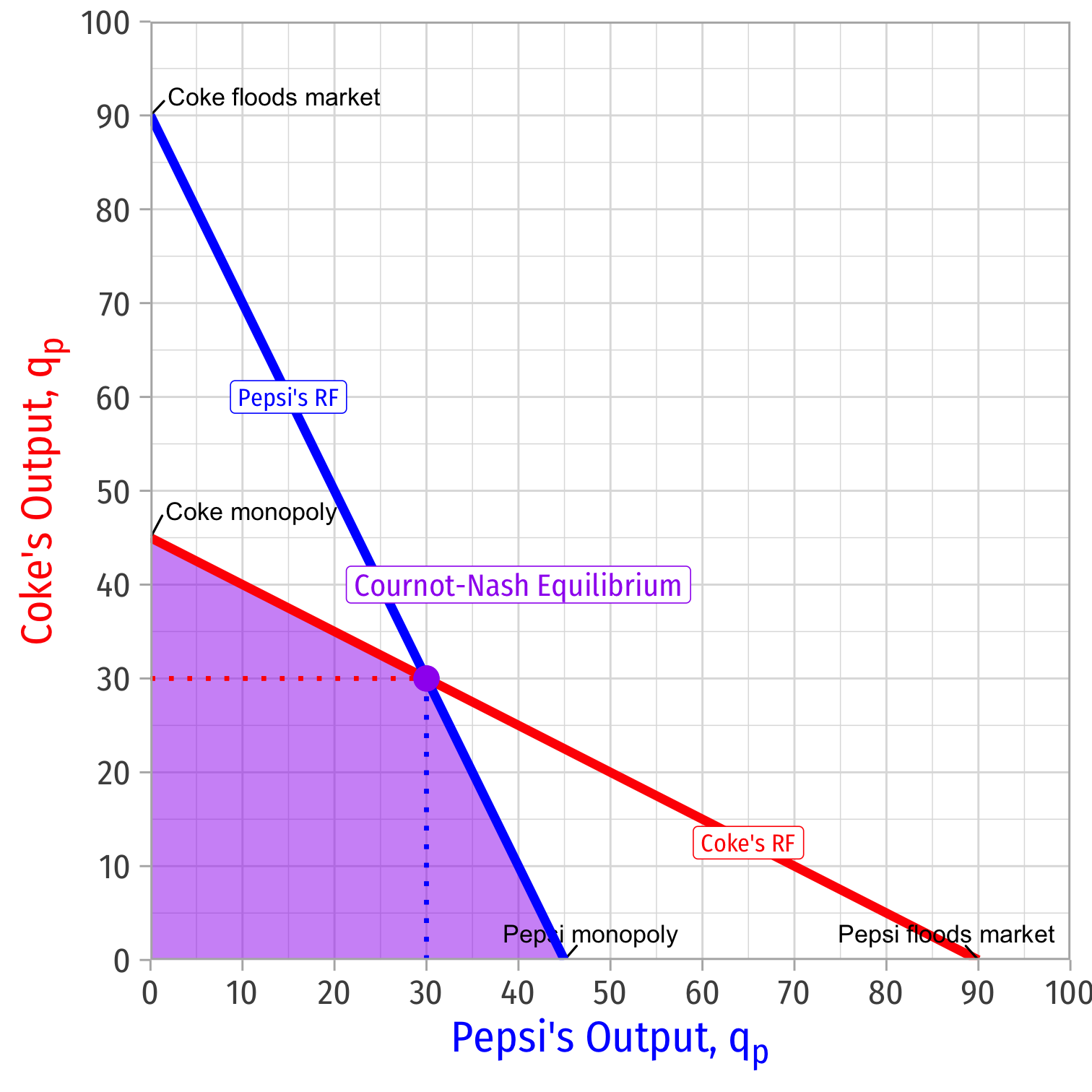
  • Case 1 (small capacities): Suppose each firm’s capacity is no larger than its Cournot best response to its competitor producing at capacity \begin{align*}k_c &\leq 30-0.5k_p \\ k_p &\leq 30-0.5k_c \\ \end{align*}

Nash Equilibrium Under Capacity Constraints

  • Nash equilibrium: p_c = p_ p = P(k_1+k_2)

    • Each firm charges the same price, produces at capacity, and the price is the market demand at their combined capacities

  • No incentive to lower price, can't produce more output (each at capacity)!

  • No incentive to raise price either

    • Best response to other firm producing at k is your Cournot best response; but not possible (beyond your capacity); raising price makes you worse off (in fact you'd like to sell more and lower your price, but you can't!)

Nash Equilibrium Where Not Capacity Constrained

  • Case 2 (no capacity constraints): Suppose each firm’s capacity is sufficient to meet the entire market demand at marginal cost pricing

  • Nash equilibrium: p_c = p_p = c

  • Both firms flood the market, charging marginal cost (back to classic Bertrand game)

Bertrand Competition with Product Differentiation

Product Differentiation

  • Now consider instead of homogenous goods, each seller is selling differentiated products (i.e. imperfect substitutes)

    • Consumers have preferences between Coke and Pepsi

  • Same assumptions of Bertrand model:

    • Firms set their own prices simultaneously

  • But now each firm faces its own downward-sloping demand curve

Product Differentiation

  • Suppose the demand for Coke and for Pepsi, respectively, are: q_c = 1.00-0.25p_c+0.25p_p \\ q_p = 1.00+0.25p_c-0.25p_p

  • Notice the positive relationship between p_p and q_c (and p_c and q_p): imperfect substitutes

Product Differentiation

  • Suppose the demand for Coke and for Pepsi, respectively, are: q_c = 1.00-0.25p_c+0.25p_p \\ q_p = 1.00+0.25p_c-0.25p_p

  • Notice the positive relationship between p_p and q_c (and p_c and q_p): imperfect substitutes

  • Solving for Coke:

MR_c = 1.00+0.25p_p-0.50p_c

Product Differentiation

  • Solving for Coke:

\begin{align*} MR_c &= MC_c \\ 1.00+0.25p_p-0.50p_c & = 0.50 \\ p_c & = 1.00 + 0.5p_p\end{align*}

  • Coke's reaction function to Pepsi's price

Product Differentiation

  • Solving for Coke:

\begin{align*} MR_c &= MC_c \\ 1.00+0.25p_p-0.50p_c & = 0.50 \\ p_c & = 1.00 + 0.5p_p\end{align*}

  • Coke's reaction function to Pepsi's price

  • Eqivalently for Pepsi:

p_p = 1.00 + 0.5 p_c

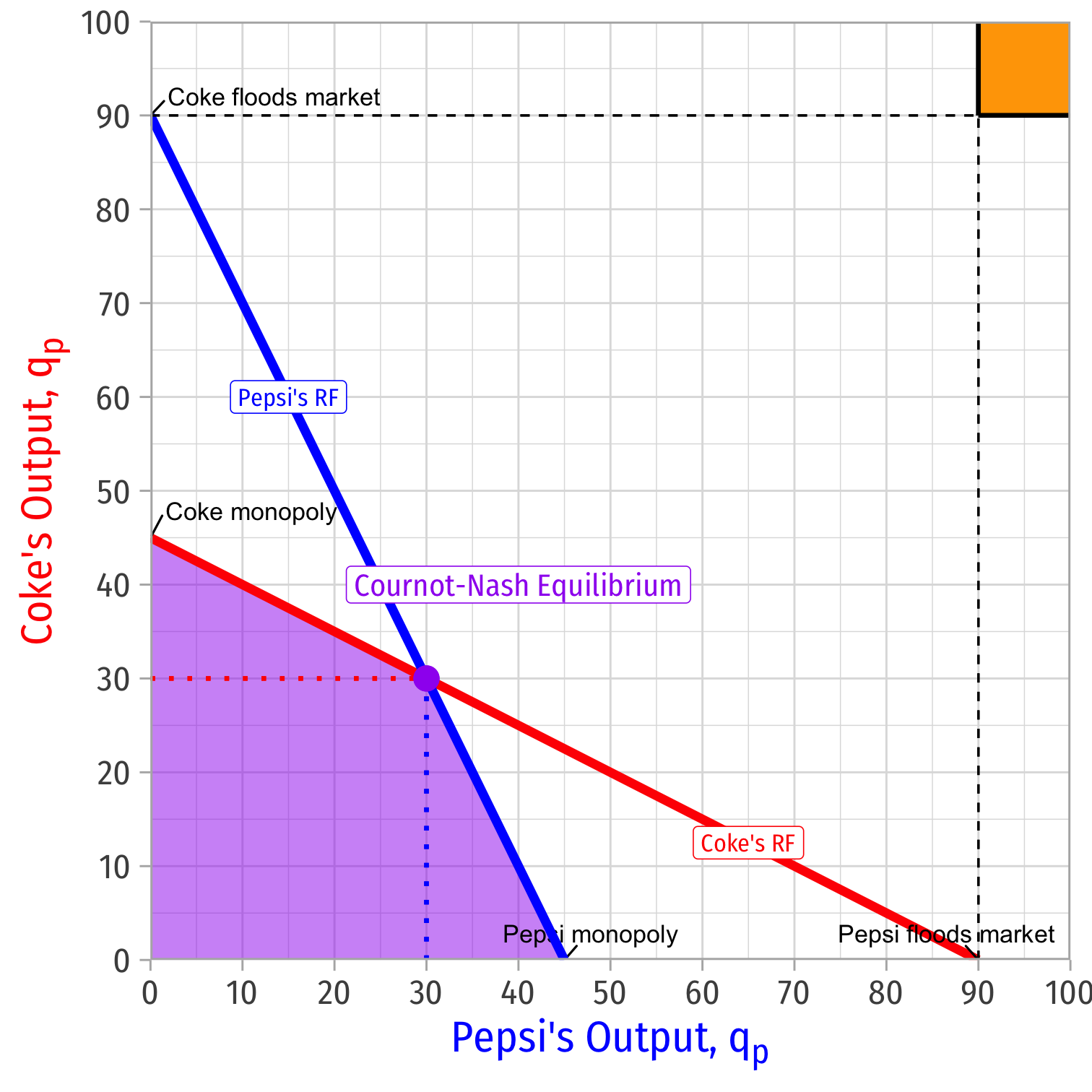
Reaction Functions and Nash Equilibrium

Reaction Functions and Nash Equilibrium: Algebraically

  • Nash Equilibrium algebraically: plug one firm's reaction function into the other's

\begin{align*} p_{c}^*&=1.00+0.5p_{p}\\ p_{p}^*&=1.00+0.5p_{c}\\ \end{align*}

Reaction Functions and Nash Equilibrium: Algebraically

  • Nash Equilibrium algebraically: plug one firm's reaction function into the other's

\begin{align*} p_{c}^*&=1.00+0.5p_{p}\\ p_{p}^*&=1.00+0.5p_{c}\\ \end{align*}

p_p^* = p_c^* = 2.00

Conjectural Variations

Cournot vs Bertrand

  • Outcomes are very different between Cournot and Bertrand competition (with homogeneous products and no capacity constraints)

    • Market power & profits with Cournot; decreases with competitors and \varepsilon
    • Perfect competition with Bertrand

  • Why? In Bertrand, firm anticipates that if it undercuts rival, can drive its sales to zero; but in Cournot it believes its rival will not change its output

Cournot vs Bertrand

  • One interpretation: consider a two-stage game between firms with homogeneous products:

    1. Firms invest in capacity (setting k_i)
    2. Firms compete over price

  • We can consider this once we learn more game theory

  • Nash equilibrium: each firm invests in capacity k_i = q_i^c, equal to it's Cournot quantity; then prices equal to producing capacity

    • Limit capacity to reduce price competition in second stage! (Larger capacity \implies more aggressive price cutting)
    • In this case, Cournot model is a “shorthand” or reduced form of this 2 stage game

Conjectural Variations

  • Cournot's best response function is traditionally called a reaction function - from his discussion about how firms respond to another's output, assuming the other firm does not change its output

Conjectural Variations

  • Cournot's best response function is traditionally called a reaction function - from his discussion about how firms respond to another's output, assuming the other firm does not change its output

  • Bowley (1924) calls this a conjecture: firm's belief about how its rivals will react to changes in its output

Conjectural Variations

  • Cournot's best response function is traditionally called a reaction function - from his discussion about how firms respond to another's output, assuming the other firm does not change its output

  • Bowley (1924) calls this a conjecture: firm's belief about how its rivals will react to changes in its output

  • Consider Cournot competition with homogenous goods, identical costs. Firm 1's marginal revenue is:

MR_1 = P + \frac{\Delta P}{\Delta Q} \frac{\Delta Q}{\Delta q_1}q_1

Conjectural Variations

MR_1(Q) = P + \frac{\Delta P}{\Delta Q} \color{#e64173}{\frac{\Delta Q}{\Delta q_1}}q_1

  • \color{#e64173}{\frac{\Delta Q}{\Delta q_1}} is the rate of change in industry output that firm 1 expects when it increases its output
    • \Delta Q = \Delta q_1 + \color{#6A5ACD}{\frac{\Delta q_2}{\Delta q_1}} \Delta q_1
    • where \color{#6A5ACD}{\frac{\Delta q_2}{\Delta q_1}} is Firm 1’s conjecture about how Firm 2 will respond to Firm 1's output change

Conjectural Variations

MR_1(Q) = P + \frac{\Delta P}{\Delta Q} \color{#e64173}{\frac{\Delta Q}{\Delta q_1}}q_1

  • \color{#e64173}{\frac{\Delta Q}{\Delta q_1}} is the rate of change in industry output that firm 1 expects when it increases its output

    • \Delta Q = \Delta q_1 + \color{#6A5ACD}{\frac{\Delta q_2}{\Delta q_1}} \Delta q_1

    • where \color{#6A5ACD}{\frac{\Delta q_2}{\Delta q_1}} is Firm 1’s conjecture about how Firm 2 will respond to Firm 1's output change

    • Divide everything by \Delta q_1:

\frac{\Delta Q}{\Delta q_1} = 1 + \color{#6A5ACD}{\nu_1}

  • where \color{#6A5ACD}{\nu_1 = \frac{\Delta q_2}{\Delta q_1}}, Firm 1's conjecture

Conjectural Variations

  • Substituting this back in, we get

MR_1(Q) = P(Q) + \frac{\Delta P(Q)}{\Delta Q} (1+ \color{#6A5ACD}{\nu_1})q_1

  • Equilibrium: each firm is profit-maximizing, given its conjecture about its rival

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu_1})q_1 = MC(q_1)

And likewise for firm 2

Conjectural Variations

  • Substituting this back in, we get

MR_1(Q) = P(Q) + \frac{\Delta P(Q)}{\Delta Q} (1+ \color{#6A5ACD}{\nu_1})q_1

  • Equilibrium: each firm is profit-maximizing, given its conjecture about its rival

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu_1})q_1 = MC(q_1)

And likewise for firm 2

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu_2})q_2 = MC(q_2)

Conjectural Variations

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu_1})q_1 = MC(q_1)

  • We can characterize effects of different conjectures on equilibrium output

  • Larger values of \color{#6A5ACD}{\nu} (more aggressive response by other firm) reduce firm's MR(q) and therefore its output

Conjectural Variations

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu})q_1 = MC(q_1)

  • Assume a common conjecture between firms \color{#6A5ACD}{\nu}=\nu_1=\nu_2

Conjectural Variations

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu})q_1 = MC(q_1)

  • Assume a common conjecture between firms \color{#6A5ACD}{\nu}=\nu_1=\nu_2
  • \nu = 0: the Cournot conjecture† (reduces to the simple Cournot model)
    • rival does not change their output when you increase yours

† Recall the definition of MR(q)= p + \frac{\Delta p}{\Delta q}q; or double the slope as demand.

Conjectural Variations

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu})q_1 = MC(q_1)

  • Assume a common conjecture between firms \color{#6A5ACD}{\nu}=\nu_1=\nu_2
  • \nu = 0: the Cournot conjecture† (reduces to the simple Cournot model)
    • rival does not change their output when you increase yours

† Recall the definition of MR(q)= p + \frac{\Delta p}{\Delta q}q; or double the slope as demand.

  • \nu = -1: the Bertrand conjecture; firm is a price-taker, setting p=MC
    • rival reduces their output to offset each increase in yours (leaving price unchanged)

Conjectural Variations

P + \frac{\Delta P}{\Delta Q} (1+ \color{#6A5ACD}{\nu})q_1 = MC(q_1)

  • Assume a common conjecture between firms \color{#6A5ACD}{\nu}=\nu_1=\nu_2
  • \nu = 1: the Collusive/monopoly conjecture, firm(s) acts like a monopolist over the industry (since 2q_1 is the total industry output)
    • rival changes their output exactly same as yours (collusive)
    • you can affect total industry output but not your market share (it will always remain constant)
    • one firm can't increase its profits at the expense of the other (i.e. cheating cartel is counterproductive)

P + \frac{\Delta P}{\Delta Q} 2q_1 = MC(q_1)

Conjectural Variations: Flaws & Benefits

  • Logical flaw in the conjectural variations model: assumes firms make decisions simultaneously, not “reacting” to each other in real time!

    • We’ll deal with dynamic responses later

  • But a useful empirical framework to explore market power and competitiveness

    • interpret and estimate \nu as a conduct parameter to see if industry performing closer to Cournot/Bertrand/Collusion
    • in general, the greater \nu is, the greater market power and markups are

Bertrand Competition: Moblab

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow