3.1 — Repeated Games & Collusion
ECON 326 • Industrial Organization • Spring 2023
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/ioS23
ioS23.classes.ryansafner.com
Reframing Oligopoly Theory
Reframing Oligopoly Theory

The “classic” models of oligopoly (Cournot & Bertrand) have significant flaws
- Primarily: static games where players only interact once
- In reality, players continue interacting and change behavior in response to previous observed behavior!
Cournot ignored the possibility of collusion (we considered it alongside Cournot's model)
- Introduced by Edward Chamberlin (1933) — The Theory of Monopolistic Competition
- It's in the interest of the firms to find a way to collude!
Reaching a Collusive Bargain
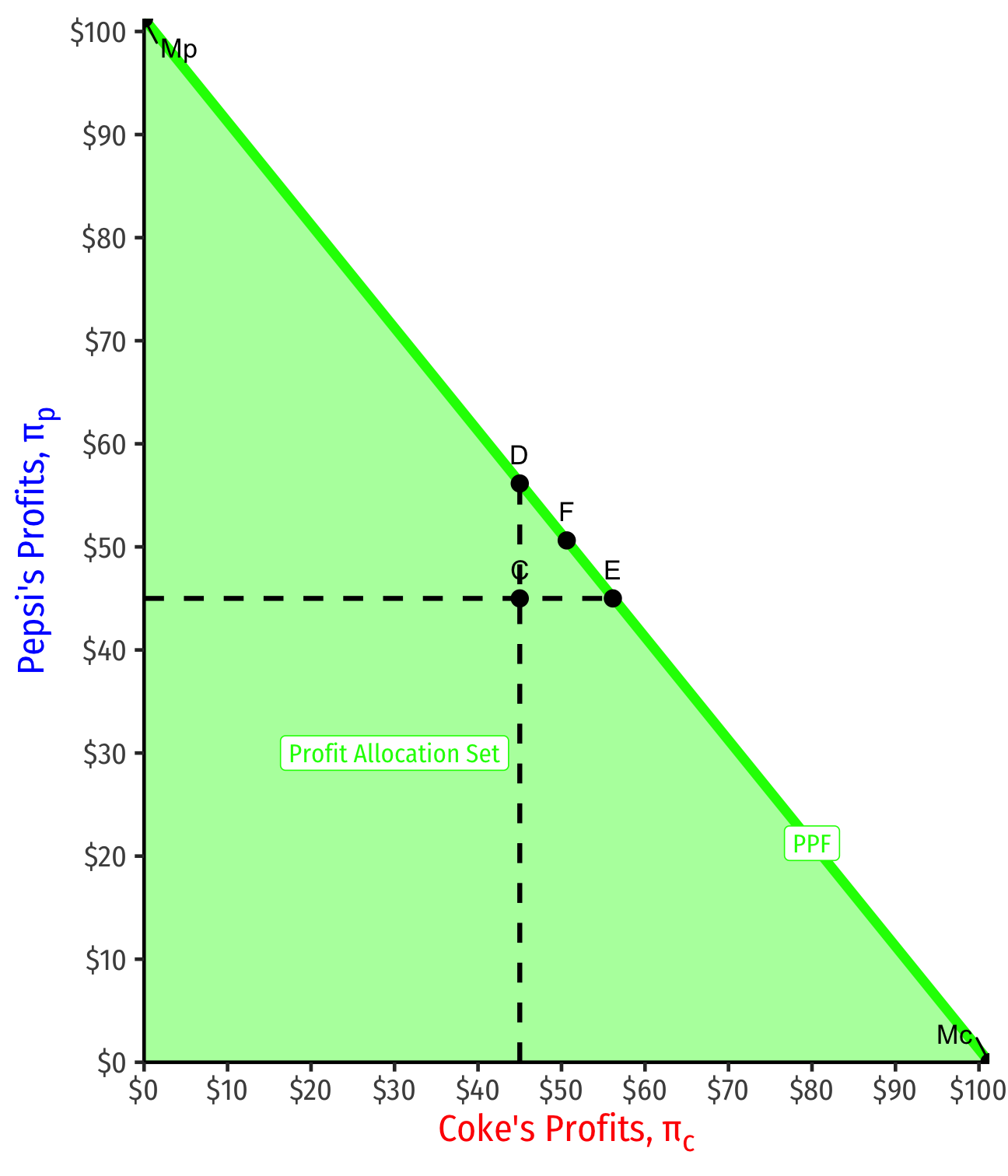
Consider a profit possibilities frontier between Coke and Pepsi should they collude
- Using our conditions from Cournot (2.2)
Point C: Cournot-Nash equilibrium
- Each firm produces 30, gets $45 in profit
Points Mc, Mp, if Coke or Pepsi were a monopolist, respectively
- One firm produces 45 (other 0), gets $101.25 in profit
Reaching a Collusive Bargain
Anything northeast of C is a Pareto improvement (for the firms)
A bargaining problem between Coke and Pepsi
Coke would prefer point E, Pepsi point D, point F is a 50:50 split
But in any case, a lot of room for a mutually-beneficial agreement to cooperate instead of (Cournot) competing
Reframing Oligopoly Theory

George Stigler
1911—1991
Economics Nobel 1982
“The present paper accepts the hypothesis that oligopolists wish to collude to maximize joint profits. It seeks to reconcile this wish with the facts, such as that collusion is impossible for many firms and collusion is much more effective in some circumstances than in others. The reconciliation is found in the problem of policing a collusive agreement, which proves to be a problem in the theory of information,” (44).
Stigler, George J, 1964, “A Theory of Oligopoly,” Journal of Political Economy 72(1): 44-61
Reframing Oligopoly Theory

George Stigler
1911—1991
Economics Nobel 1982
“We shall show that collusion normally involves much more than ‘the’ price...The colluding firms must agree upon the price structure appropriate to the transaction classes which they are prepared to recognize. A complete profit-maximizing price structure may have almost infinitely numerous price classes: the firms will have to decide upon the number of price classes in the light of the costs and returns from tailoring prices to the diversity of transactions,” (44-46).
Reframing Oligopoly Theory

George Stigler
1911—1991
Economics Nobel 1982
“Let us assume that the collusion has been effected, and a price structure agreed upon. It is a well-established proposition that if any member of the agreement can secretly violate it, he will gain larger profits than by conforming to it. It is, moreover, surely one of the axioms of human behavior that all agreements whose violation would be profitable to the violator must be enforced. The literature of collusive agreements...is replete with instances of the collapse of conspiracies because of ‘secret’ price-cutting. This literature is biased: conspiracies that are successful in avoiding an amount of price-cutting which leads to collapse of the agreement are less likely to be reported or detected. But no conspiracy can neglect the problem of enforcement,” (46)
Reframing Oligopoly Theory

George Stigler
1911—1991
Economics Nobel 1982
“Enforcement consists basically of detecting significant deviations from the agreed-upon prices. Once detected, the deviations will tend to disappear because they are no longer secret and will be matched by fellow conspirators if they are not withdrawn. If the enforcement is weak, however — if price-cutting is detected only slowly and incompetently — the conspiracy must recognize its weakness: it must set prices not much above the competitive level so the inducements to price-cutting are small...” (46).
Reframing Oligopoly Theory

George Stigler
1911—1991
Economics Nobel 1982
“Policing the collusion sounds very much like the subtle and complex problem presented in a good detective story. [But] there is a difference: In our case the man who murders the collusive price will recieve the bequest of patronage. The basic method of detection of a price-cutter must be the fact that he is getting business he would not otherwise obtain,” (47).
Reframing Oligopoly Theory

George Stigler
1911—1991
Economics Nobel 1982
We should focus oligopoly theory less on static models of Cournot/Bertrand/etc competition
Focus more on examining the types of conditions where firms can effectively form and maintain collusive agreements, and conditions where agreements break down into competition
- Stigler (1964) specifically focused on the problem of a cartel policing against “secret price cutting”
Consider more of a dynamic game of cooperation and/or competition between firms
More Game Theory
Game Theory: Some Generalizations

See my game theory course for more
There's a lot more to game theory than a one-shot prisoners' dilemma:
one shot vs. repeated game
discrete vs. continuous strategies
perfect vs. imperfect vs. incomplete/asymmetric information
simultaneous vs. sequential games
Solution Concepts

We use various “solution concepts” to allow us to predict an equilibrium of a game
Nash Equilibrium is the primary solution concept
- Note it has many variants depending on type of game!
Recall, Nash Equilibrium: no players want to change their strategy given what everyone else is playing
- All players are playing a best response to each other
Solution Concepts: Nash Equilibrium

- Important about Nash equilibrium:
N.E. ≠ the “best” or optimal outcome
- Recall the Prisoners' Dilemma!
Game may have multiple N.E.
Game may have no N.E. (in “pure” strategies)
Example: Coordination Game

- A Coordination Game
- No dominant strategies
Example: Coordination Game

- Two Nash equilibria: (A,A) and (B,B)
- Either just as good
- Coordination is most important
Example: Coordination Game

- Two general methods to solve for Nash equilibria:
1) Cell-by-Cell Inspection: look in each cell, does either player want to deviate?
- If no: a Nash equilibrium
- If yes: not a Nash equilibrium
Example: Coordination Game

- Two general methods to solve for Nash equilibria:
2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?
- Ties are allowed
- Any cell where both players are playing a best response is a Nash Equilibrium
Example: Coordination Game

Player 1's best responses
- Two general methods to solve for Nash equilibria:
2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?
- Ties are allowed
- Any cell where both players are playing a best response is a Nash Equilibrium
Example: Coordination Game

Player 2's best responses
- Two general methods to solve for Nash equilibria:
2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?
- Ties are allowed
- Any cell where both players are playing a best response is a Nash Equilibrium
Example: Coordination Game

N.E.: each player is playing a best response
- Two general methods to solve for Nash equilibria:
2) Best-Response Analysis: take the perspective of each player. If the other player plays a particular strategy, what is your strategy(s) that gets you the highest payoff?
- Ties are allowed
- Any cell where both players are playing a best response is a Nash Equilibrium
A Change in the Game

Two Nash equilibria again: (A,A) and (B,B)
But here (A,A) ≻ (B,B)!
A Change in the Game

Path Dependence: early choices may affect later ability to choose or switch
Lock-in: the switching cost of moving from one equilibrium to another becomes prohibitive
Suppose we are currently in equilibrium (B,B)
Inefficient lock-in:
- Standard A is superior to B
- But too costly to switch from B to A
Introduction to Sequential Games
Sequential Games
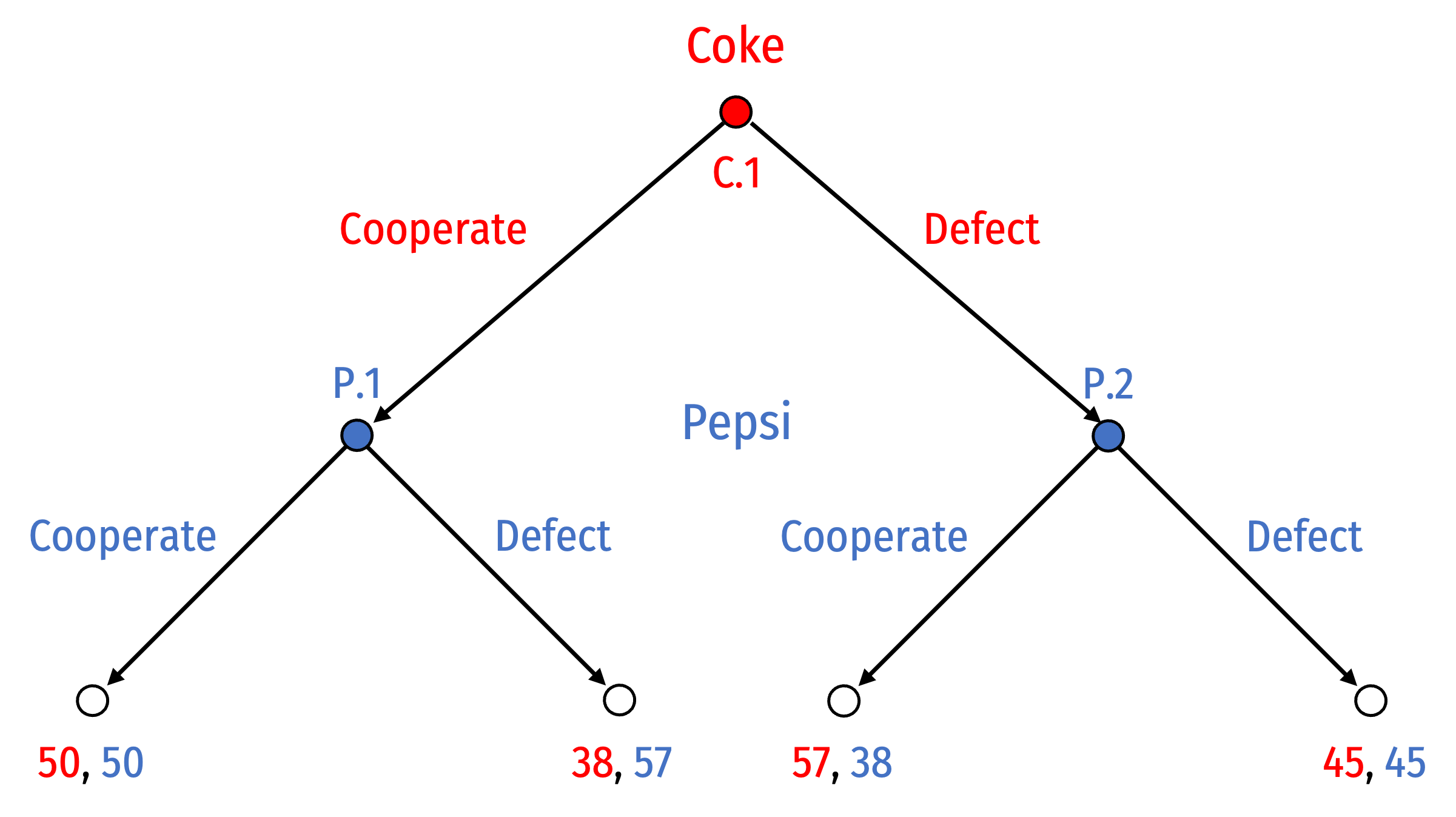
Consider a sequential game of Cournot competition between Coke and Pepsi
Coke moves first, then Pepsi, then the game ends
Each player can:
- Cooperate: produce cartel quantity (22.5)
- Defect: produce Cournot quantity (30)
Sequential Games
Designing a game tree:
Decision nodes: decision point for each player
- Solid nodes, I've labeled and color-coded by player (C.1, P.1, P.2)
Terminal nodes: outcome of game, with payoff for each player (profits)
- Hollow nodes, no further choices

Sequential Games
- Four possible outcomes:
- (Cooperate, Cooperate): 50, 50
- (Cooperate, Defect): 38, 57
- (Defect, Cooperate): 57, 38
- (Defect, Defect): 45, 45

Strategies
(“Pure”) strategy†: a player’s complete plan of action for every possible contingency
- i.e. what player will choose at every possible decision node, even if it’s never reached
Think of a strategy like an algorithm:
If we reach node 1, then I will play X; if we reach node 2, then I will play Y; if...

† “Pure” is meant to contrast against “mixed” strategies, where players take a range of actions according to a probability distribution. That's beyond the scope of this class.
Strategies
- Coke has 21=2 possible strategies:
- Cooperate at C.1
- Defect at C.1

Strategies
Coke has 21=2 possible strategies:
- Cooperate at C.1
- Defect at C.1
Pepsi has 22=4 possible strategies:
- (Cooperate at P.1, Cooperate at P.2)
- (Cooperate at P.1, Defect at P.2)
- (Defect at P.1, Cooperate at P.2)
- (Defect at P.1, Defect at P.2)

Solving the Game: Backward Induction
Solve a sequential game by “backward induction” or “rollback”
To determine the outcome of the game, start with the last-mover (i.e. decision nodes just before terminal nodes) and work to the beginning
A process of considering “sequential rationality”:
“If I play X, my opponent will respond with Y; given their response, do I really want to play X?”
- What is that mover's best choice to maximize their payoff?

Solving the Game: Backward Induction
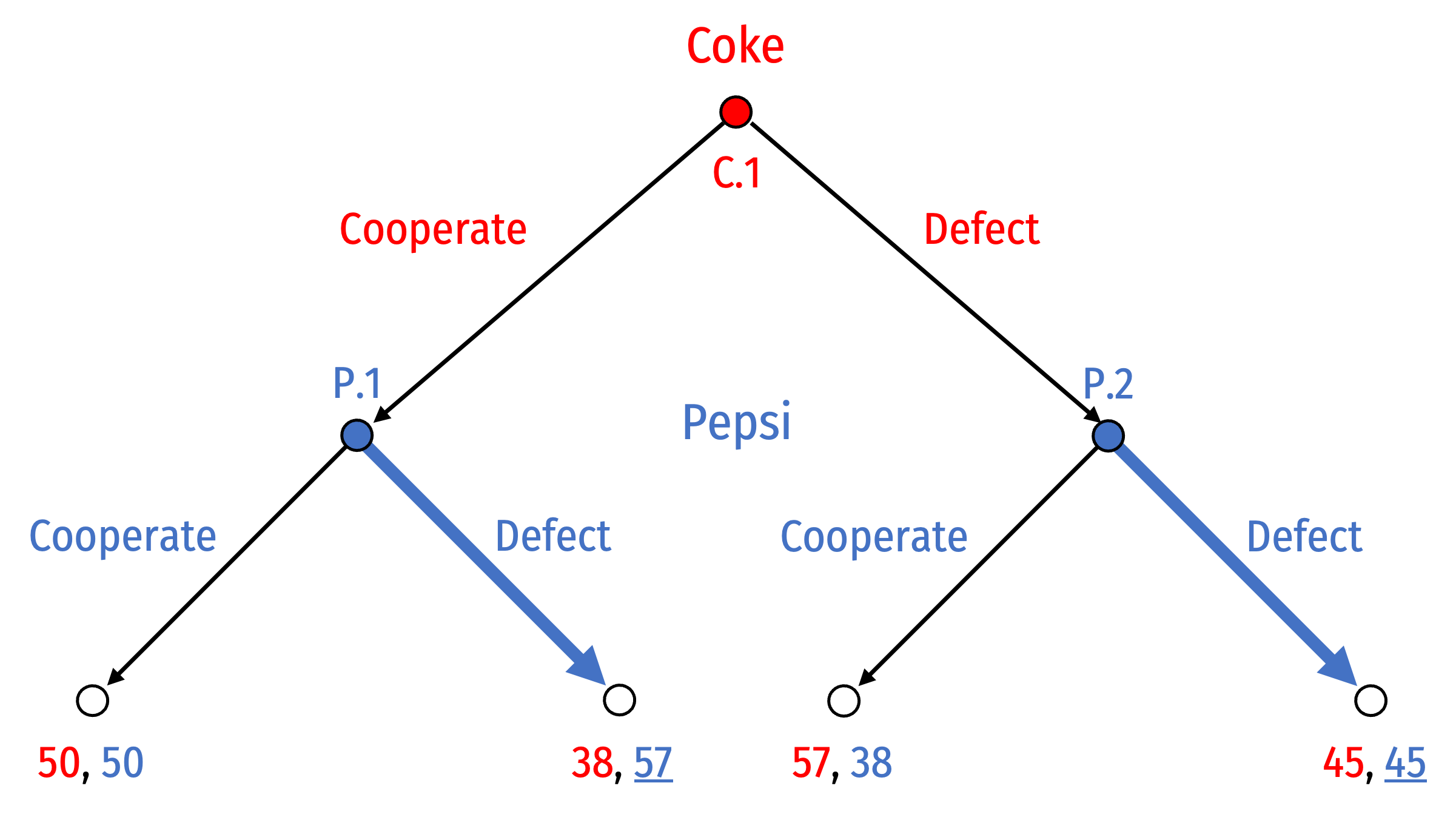
We start at P.1 where Pepsi can:
- Cooperate to yield outcome (50, 50)
- Defect to yield outcome (38, 57)
And P.2 where Pepsi can:
- Cooperate to yield outcome (57, 38)
- Defect to yield outcome (45, 45)
Solving the Game: Backward Induction
Pepsi will Defect if the game reaches node P.1 and Defect if the game reaches node P.2
Recognizing this, what will Coke do?

Solving the Game: Backward Induction
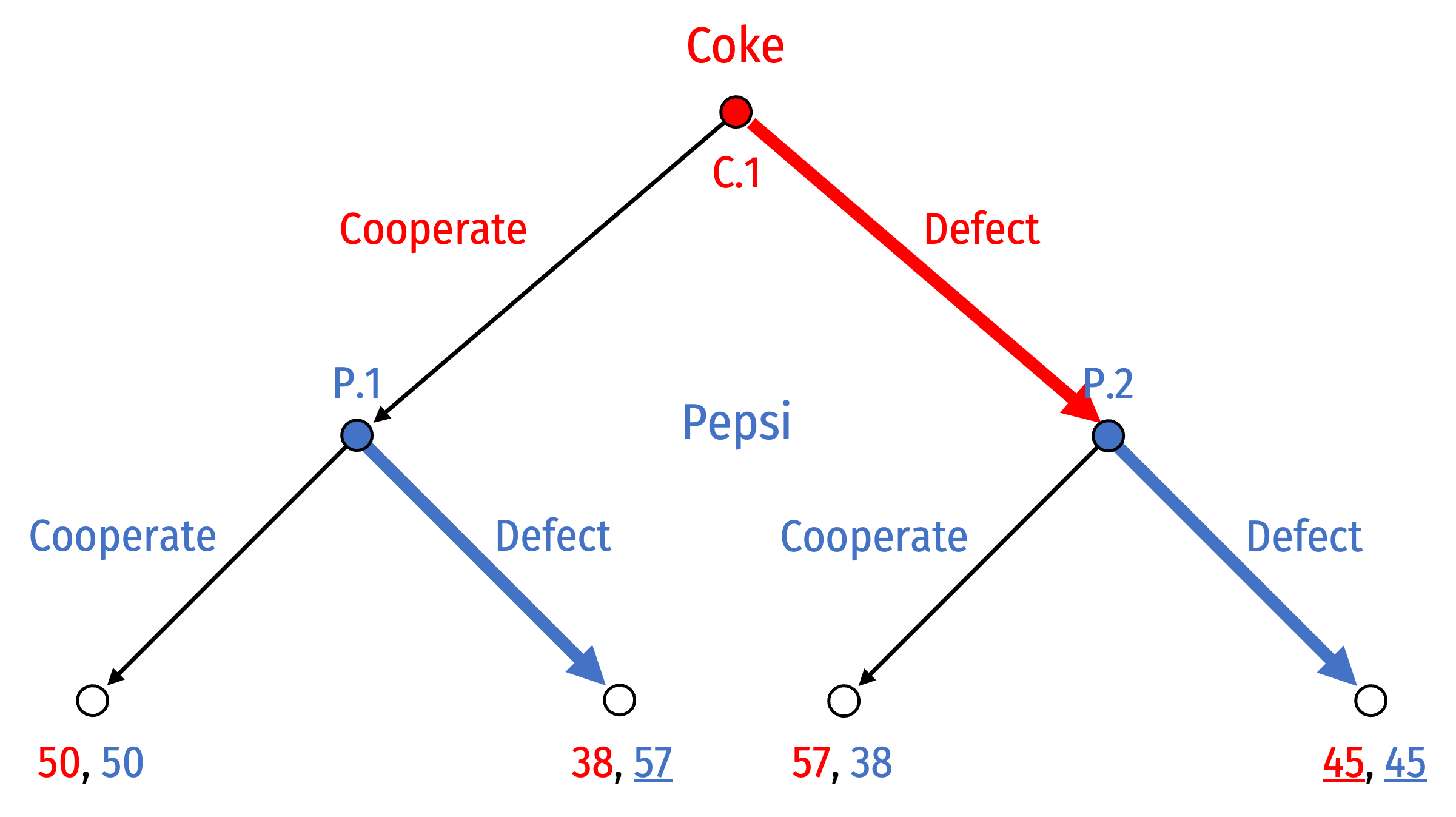
- Work our way up to C.1 where Coke can:
- Cooperate, knowing Pepsi will Defect, to yield outcome (38, 57)
- Defect, knowing Pepsi will Defect, to yield outcome (45, 45)
Solving the Game: Backward Induction
- Nash Equilibrium:
(Defect, (Defect, Defect))

Solving the Game: Pruning the Tree
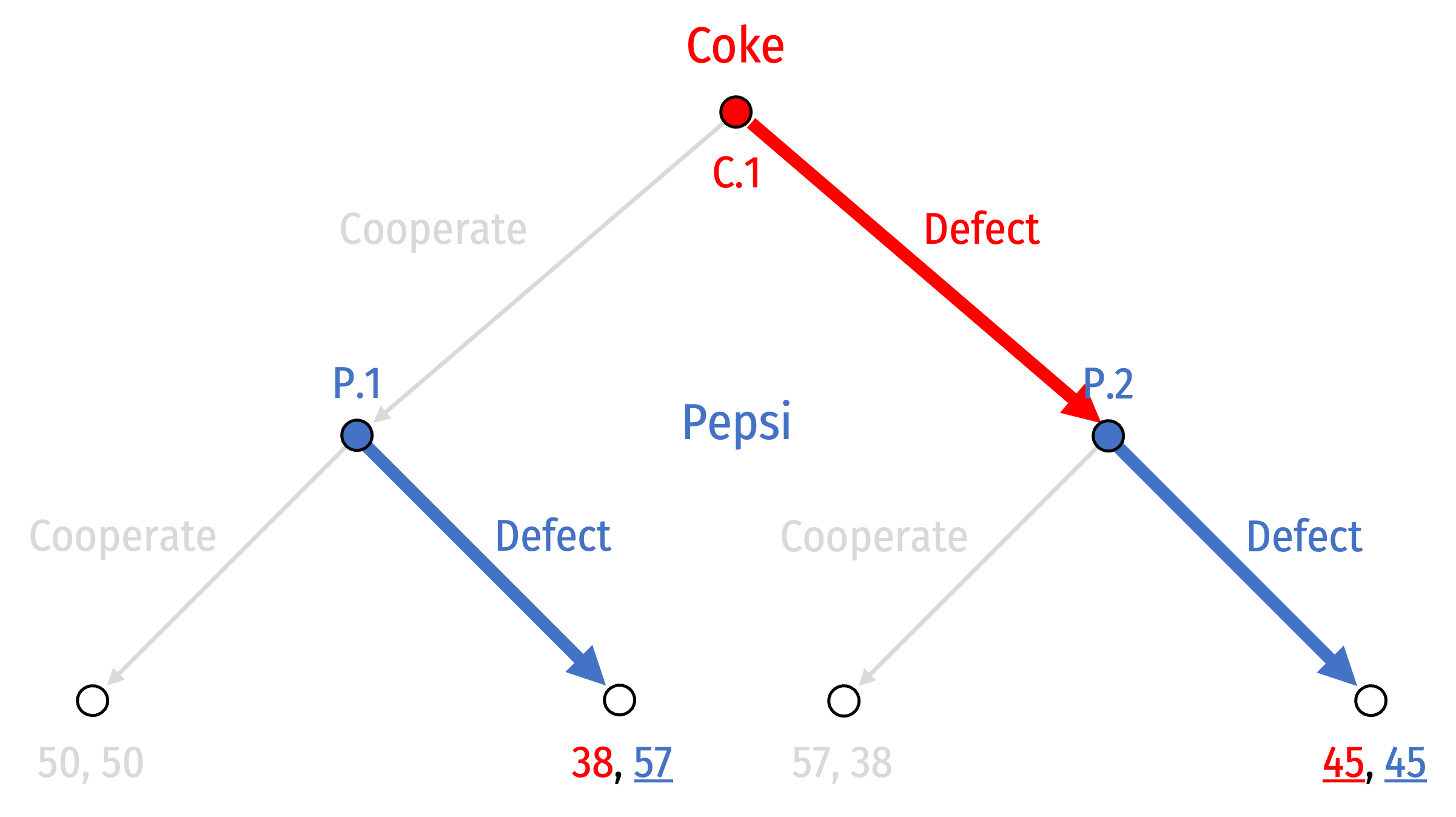
As we work backwards, we can prune the branches of the game tree
- Highlight branches that players will choose
- Cross out branches that players will not choose
Equilibrium path of play is highlighted from the root to one terminal node
- All other paths are not taken
Repeated Games
Prisoners' Dilemma, Reprise
A true prisoners' dilemma: a>b>c>d
Each player's preferences:
- 1st best: you Defect, they Coop. ("temptation payoff")
- 2nd best: you both Coop.
- 3rd best: you both Defect
- 4th best: you Coop., they Defect ("sucker's payoff")
Nash equilibrium: (Defect, Defect)
- (Coop., Coop.) an unstable Pareto improvement
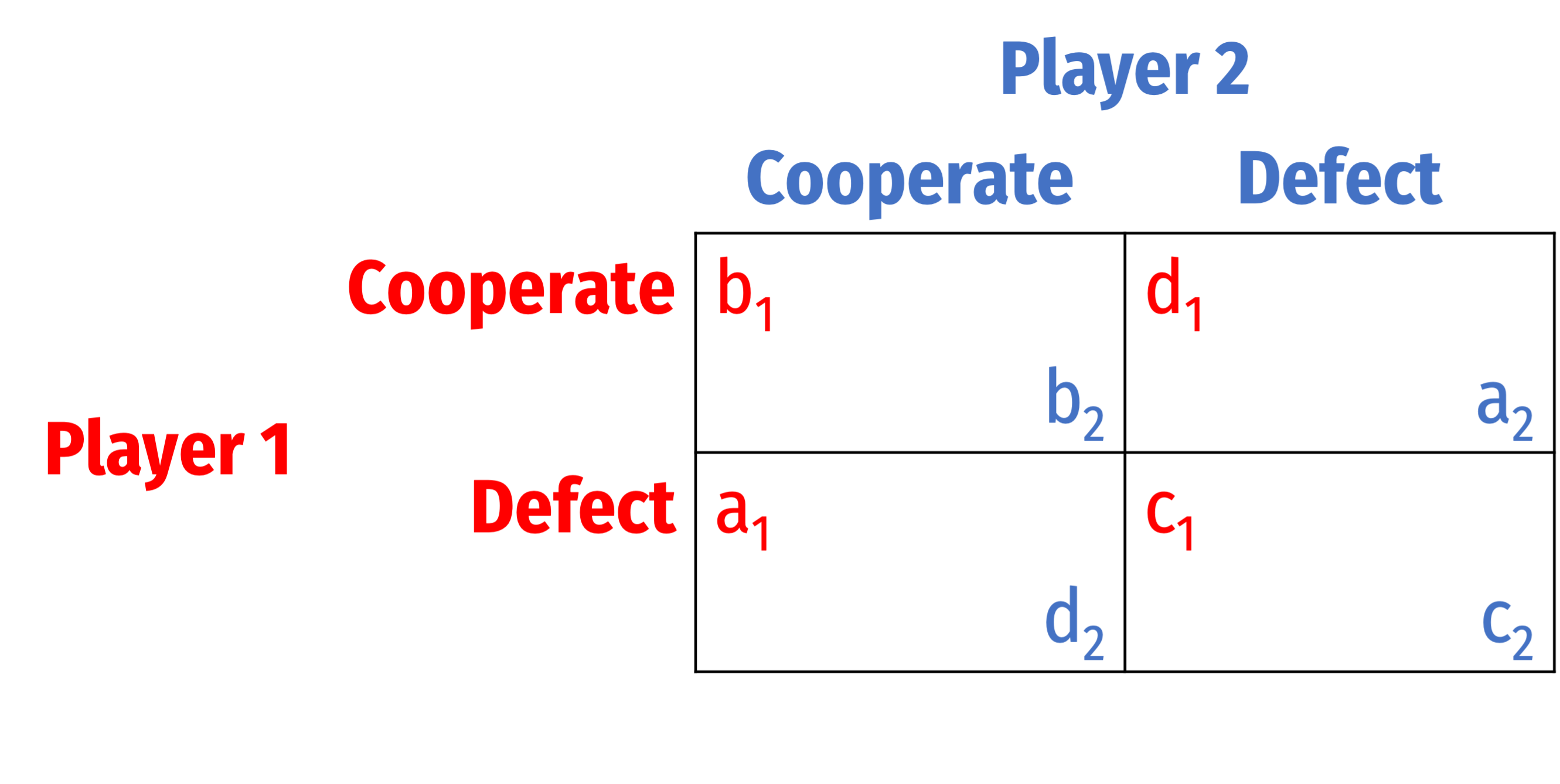
Prisoners' Dilemma: How to Sustain Cooperation?
We'll stick with these specific payoffs for this lesson
How can we sustain cooperation in Prisoners' Dilemma?

Repeated Games: Finite and Infinite
Analysis of games can change when players encounter each other more than once
Repeated games: the same players play the same game multiple times, two types:
Players know the history of the game with each other
Finitely-repeated game: has a known final round
Infinitely-repeated game: has no (or an unknown) final round
Finitely-Repeated Games
Finitely-Repeated Prisoners' Dilemma
Suppose a prisoners' dilemma is played for 2 rounds
Apply backwards induction:
- What should each player do in the final round?

Finitely-Repeated Prisoners' Dilemma
Suppose a prisoners' dilemma is played for 2 rounds
Apply backwards induction:
- What should each player do in the final round?
- Play dominant strategy: Defect
- Knowing each player will Defect in round 2/2, what should they do in round 1?

Finitely-Repeated Prisoners' Dilemma
Suppose a prisoners' dilemma is played for 2 rounds
Apply backwards induction:
- What should each player do in the final round?
- Play dominant strategy: Defect
- Knowing each player will Defect in round 2/2, what should they do in round 1?
- No benefit to playing Cooperate
- No threat punish Defection!

Finitely-Repeated Prisoners' Dilemma
Suppose a prisoners' dilemma is played for 2 rounds
Apply backwards induction:
Both Defect in round 1 (and round 2)
No value in cooperation over time!

Finitely-Repeated Prisoners' Dilemma
Paradox of repeated games: for any game with a unique Nash equilibrium (in pure strategies) in a one-shot game, as long as there is a known, finite end, Nash equilibrium is the same
Sometimes called Selten’s “chain-store paradox” from a famous paper by Reinhard Selten (1978)
In experimental settings, we tend to see people cooperate in early rounds, but close to the final round (if not the actual final round), defect on each other
Selten, Reinhard, (1978), “The chain store paradox,” Theory and Decision 9(2): 127–159

Infinitely-Repeated Games
“Infinitely”-Repeated Games
Finitely-repeated games are interesting, but rare
- How often do we know for certain when a game/relationship we are in will end?
Some predictions for finitely-repeated games don't hold up well in reality
We often play games or are in relationships that are indefinitely repeated (have no known end), we call them infinitely-repeated games
Infinitely-Repeated Games
- There are two nearly identical interpretations of infinitely repeated games:
- Players play forever, but discount (payoffs in) the future by a constant factor
- Each round the game might end with some constant probability
First Intepretation: Discounting the Future
Since we are dealing with payoffs in the future, we have to consider players' time preferences
Easiest to consider with monetary payoffs and the time value of money that underlies finance
PV=FV(1+r)t
FV=PV(1+r)t

Present vs. Future Goods
- Example: what is the present value of getting $1,000 one year from now at 5% interest?
PV=FV(1+r)nPV=1000(1+0.05)1PV=10001.05PV=$952.38
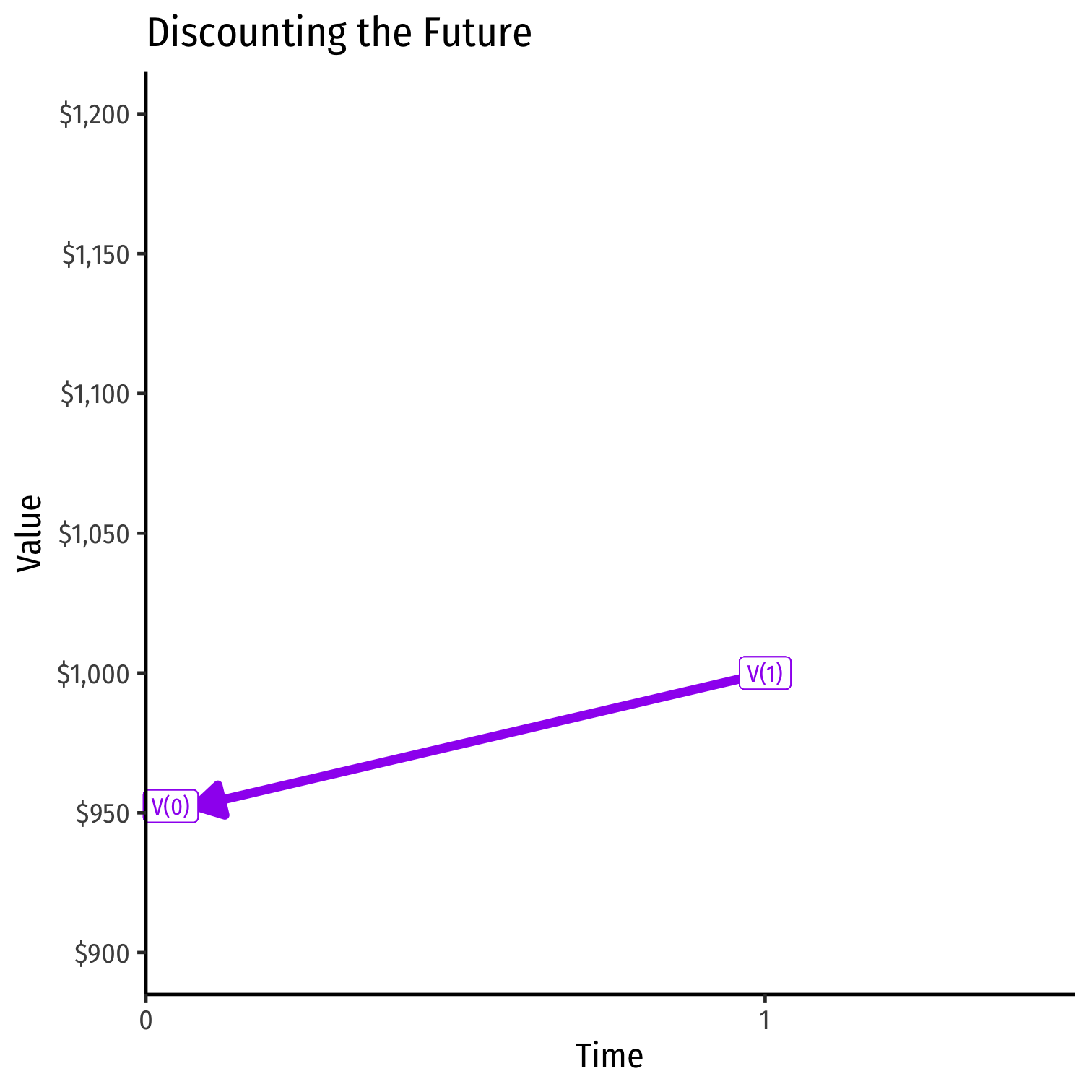
Present vs. Future Goods
- Example: what is the future value of $1,000 lent for one year at 5% interest?
FV=PV(1+r)nFV=1000(1+0.05)1FV=1000(1.05)FV=$1,050
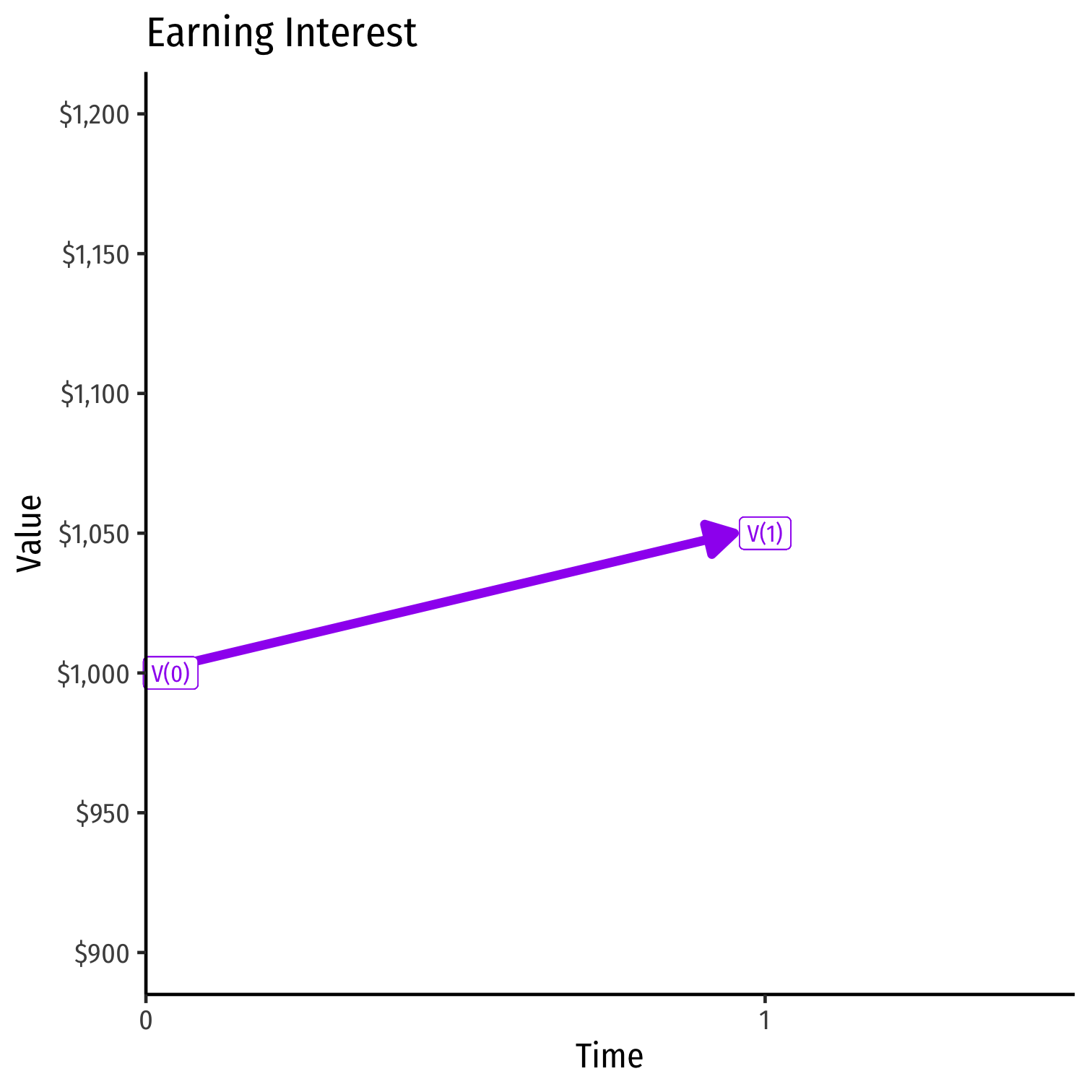
Discounting the Future
Suppose a player values $1 now as being equivalent to some amount with interest 1(1+r) one period later
- i.e. $1 with an r% interest rate over that period
The “discount factor” is δ=11+r, the ratio that future value must be multiplied to equal present value

Discounting the Future
$1 now=δ$1 later
If δ is low (r is high)
- Players regard future money as worth much less than present money, very impatient
- Example: δ=0.20, future money is worth 20% of present money
If δ is high (r is low)
- Players regard future money almost the same as present money, more patient
- Example: δ=0.80, future money is worth 80% of present money

Discounting the Future
Example: Suppose you are indifferent between having $1 today and $1.10 next period
Discounting the Future
Example: Suppose you are indifferent between having $1 today and $1.10 next period
$1 today=δ$1.10 next period$1$1.10=δ0.91≈δ
Discounting the Future
Example: Suppose you are indifferent between having $1 today and $1.10 next period
$1 today=δ$1.10 next period$1$1.10=δ0.91≈δ
There is an implied interest rate of r=0.10
$1 at 10% interest yields $1.10 next period
δ=11+rδ=11.10 ≈0.91
Discounting the Future
- Now consider an infinitely repeated game
Discounting the Future
- Now consider an infinitely repeated game
- If a player receives payoff p in every future round, the present value of this infinite payoff stream is
p(δ1+δ2+δ3+⋯+δT)
- This is due to compounding interest over time
Discounting the Future
- Now consider an infinitely repeated game
- If a player receives payoff p in every future round, the present value of this infinite payoff stream is
p(δ1+δ2+δ3+⋯+δT)
- This is due to compounding interest over time
- This infinite sum converges to:
∞∑t=1=p1−δ
- Thus, the present discounted value of receiving p forever is (p1−δ)
Prisoners' Dilemma, Infinitely Repeated
- With these payoffs, the present value of both cooperating forever is (501−δ)
- Present value of both defecting forever is (451−δ)

Alternatively: Game Continues Probabilistically
Alternate interpretation: game continues with some (commonly known among the players) probability θ each round
Assume this probability is independent between rounds (i.e. one round continuing has no influence on the probability of the next round continuing, etc)
Alternatively: Game Continues Probabilistically
Then the probability the game is played T rounds from now is θT
A payoff of p in every future round has a present value of p(θ1+θ2+θ3+⋯)=(p1−θ)
Note this is similar to discounting of future payoffs (at a constant rate); equivalent if θ=δ
Strategies in Infinitely Repeated Games
Recall, a strategy is a complete plan of action that describes how you will react under all possible circumstances (i.e. moves by other players)
- i.e. “if other player plays x, I'll play a, if they play y, I'll play b, if, ..., etc”
- think about it as a(n infinitely-branching) game tree, “what will I do at each node where it is my turn?”
For an infinitely-repeated game, an infinite number of possible strategies exist!
We will examine a specific set of contingent or trigger strategies


Trigger Strategies
Consider one (the most important) trigger strategy for an infinitely-repeated prisoners' dilemma, the “Grim Trigger” strategy:
- On round 1: Cooperate
- Every future round: so long as the history of play has been (Coop, Coop) in every round, play Cooperate. Otherwise, play Defect forever.
“Grim” trigger strategy leaves no room for forgiveness: one deviation triggers infinite punishment, like the sword of Damocles

Payoffs in Grim Trigger Strategy
- If you are playing the Grim Trigger strategy, consider your opponent's incentives:
- If you both Cooperate forever, you receive an infinite payoff stream of 50 per round
50+50δ1+50δ2+50δ3+⋯+50δ∞=501−δ

Payoffs in Grim Trigger Strategy
- This strategy is a Nash equilibrium as long there's no incentive to deviate:
Payoff to cooperation>Payoff to one-time defection501−δ>57+45δ1−δδ>0.583
- If δ>0.583, then player will cooperate and a one-time defection is not profitable

Payoffs in Grim Trigger Strategy
- δ>0.583 is sufficient to sustain cooperation under the grim trigger strategy
- This is the most extreme strategy with the strongest threat

Payoffs in Grim Trigger Strategy
- Two interpretations of δ>0.583 as a sufficient condition for cooperation:
- δ as sufficiently high discount rate
- Players are patient enough and care about the future (reputation, etc), will not defect
- δ as sufficiently high probability of repeat interaction
- Players expect to encounter each other again and play future games together

Cooperation with the Grim Trigger Strategy, In General
In general, can sustain cooperation (under grim trigger strategy) when δ>b−ac−a
Thus, cooperation breaks down (or is strengthened) when:
- a (the temptation payoff) increases (decreases)
- b (the cooperative payoff) decreases (increases)
- c (the defection payoff) increases (decreases)

Other Trigger Strategies
- “Grim Trigger” strategy is, well, grim: a single defection causes infinite punishment with no hope of redemption
- Very useful in game theory for understanding the “worst case scenario” or the bare minimum needed to sustain cooperation!
- Empirically, most people aren't playing this strategy in life
- Social cooperation hangs on by a thread: what if the other player makes a mistake? Or you mistakenly think they Defected?
- There are “nicer” trigger strategies

"Nicer" Strategies
- Consider the "Tit for Tat" strategy:
- On round 1: Cooperate
- Every future round: Play the strategy that the other player played last round
- .hi-green[Example]: if they Cooperated, play Cooperate; if they Defected, play Defect

The Evolution of Cooperation

Robert Axelrod
1943—
- Research in explaining the evolution of cooperation
- Use prisoners' dilemma to describe human societies and evolutionary biology of animal behaviors
- Hosted a series of famous tournaments for experts to submit a strategy to play in an infinitely1 repeated prisoners' dilemma
“The contestants ranged from a 10-year-old computer hobbyist to professors of computer science, economics, psychology, mathematics, sociology, political science, and evolutionary biology.”
- The Evolution of Cooperation (1984)
- Among the most cited works in all of political science
1 Each round had a 0.00346 probability of ending the game, ensuring on average 200 rounds of play
Axelrod, Robert, 1984, *The Evolution of Cooperation
The Evolution of Cooperation

Robert Axelrod
1943—
Axelrod's discussion of successful strategies based on four properties:
- Niceness: cooperate, never be the first to defect
- Be Provocable: don't be suckered by being too nice, return defection with defection
- Don't be envious: focus on maximizing your own score, rather than ensuring your score is higher than your "partner's"
- Don't be too clever: clarity is essential for others to cooperate with you
The winning strategy was, famously, TIT FOR TAT, submitted by Anatol Rapoport
Folk Theorem: Simply Put
- Folk theorem (simplified): Many strategies can sustain long-run cooperation if:
- Each player can observe history
- The value of future interactions must be sufficiently important to players
- sufficiently high discount rate δ
- sufficiently high probability of game continuing θ
- If this is true, many strategies can sustain long-run cooperation
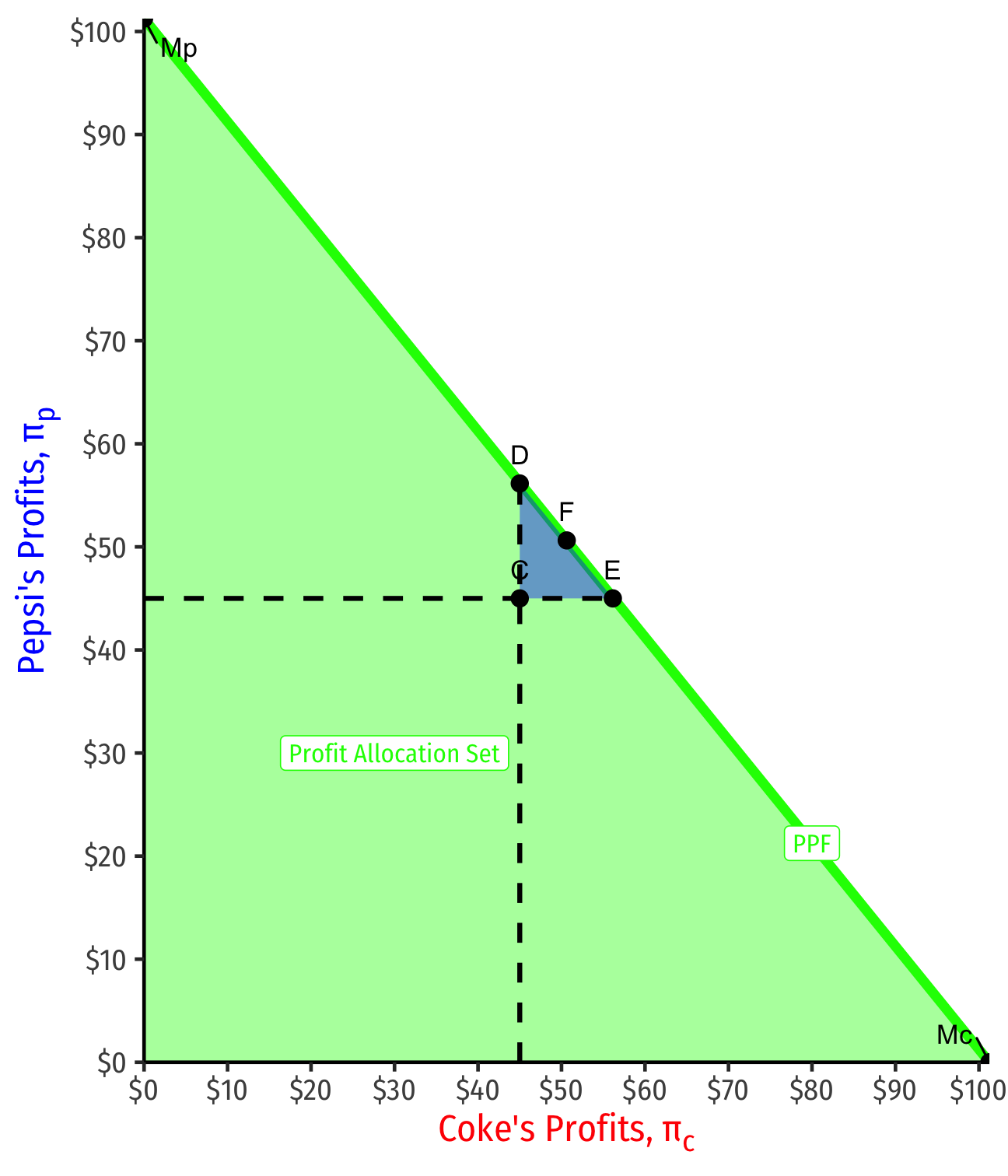
- Any in the teal set in the diagram before
- Grim trigger is simply the bare minimum/worst case scenario (and, importantly, easiest to model!)