3.3 — Entry Deterrence
ECON 326 • Industrial Organization • Spring 2023
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/ioS23
ioS23.classes.ryansafner.com
Limit Pricing
Accommodation vs. Deterrence

Henrich von Stackelberg
1905-1946
In the Stackelberg game, we implicitly assumed the Leader (Coke) would accommodate the Follower (Pepsi)
- Consider the Leader as the incumbent (firm already in the industry) and the Follower as a (potential) Entrant
In Stackelberg, Leader produced more than Cournot, but anticipated follower still entering and producing (pushing down the market price and profits below the monopoly level)
Accommodation vs. Deterrence
But there is another possibility, that the Incumbent can deter entry (a “blockaded monopoly”)
- Follower will stay out if it expects zero or negative post-entry profits π2(R2(qL1),qL1)=0
- R2 is Firm 2's Cournot reaction function
- qL1 is the “limit output”
We can find the limit output qL1 and limit price P(qL1) that successfully deters Firm 2 from entering

Entry Deterrence Example: Constant Returns to Scale
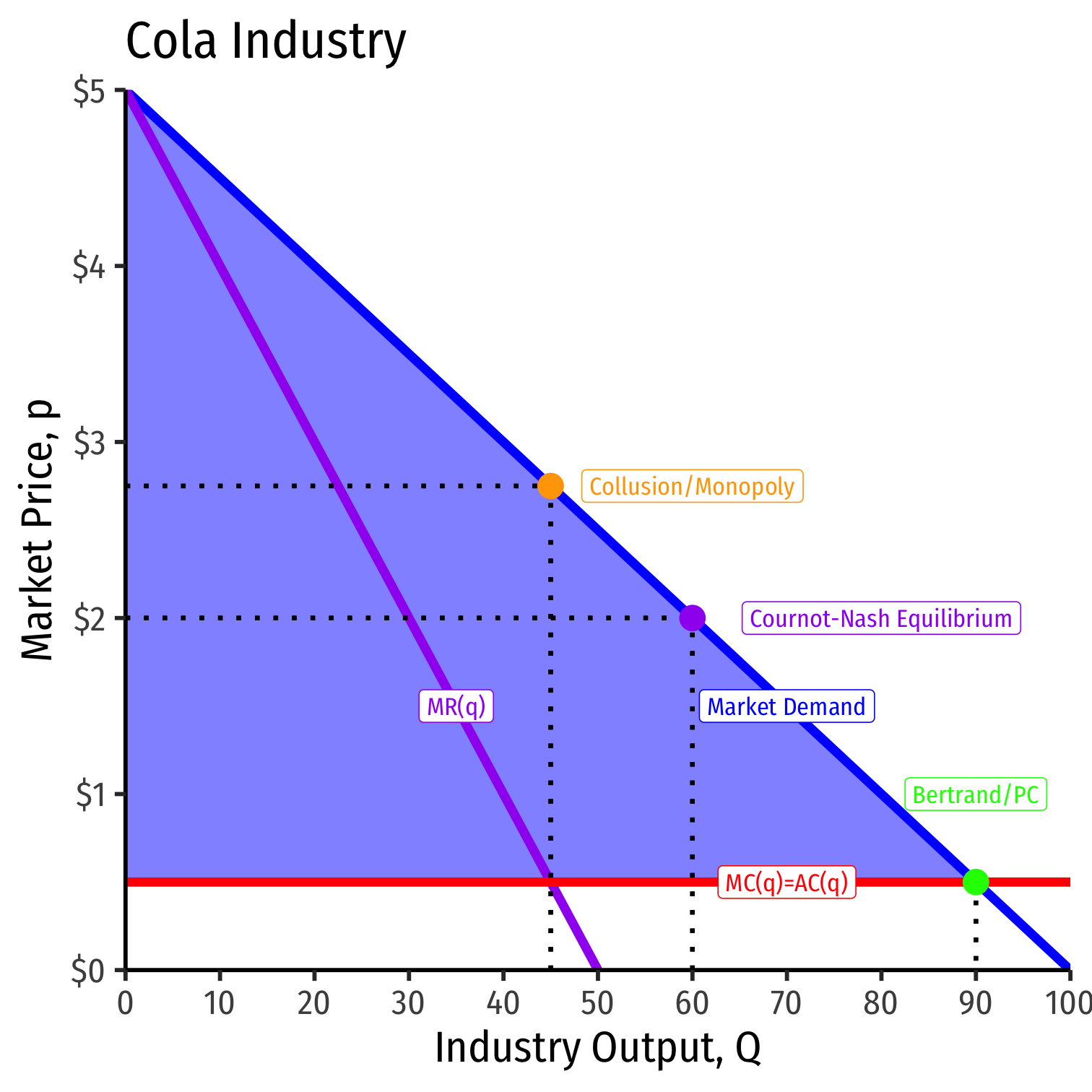
Example: Return to Coke and Pepsi again, with a constant marginal cost of $0.50 and the (inverse) market demand:
P=5−0.05QQ=qc+qp
- With Coke moving first, what level of output qLc will deter Pepsi from entering?

Entry Deterrence Example: Constant Returns to Scale
- Recall the reaction functions:
q∗c=45−0.5qpq∗p=45−0.5qc
Entry Deterrence Example: Constant Returns to Scale
- Recall the reaction functions:
q∗c=45−0.5qpq∗p=45−0.5qc
- Take Pepsi’s profit function and substitute in the demand for P, and Pepsi’s reaction function into its output qp; set profit equal to 0
- Solve carefully! (Need the quadratic formula!)
πp=(p−c)qpπp=(a−bqc−bqp−c)qpπp=(5−0.05qc−0.05qp−0.50)qpπp=(5−0.05qc−0.05[45−0.5qc]−0.50)[45−0.5qc]=(5−0.05qc−2.25+0.025qc−0.5)[45−0.5qc]=(2.25−0.025qc)[45−0.5qc]=(101.25−1.125qc−1.125qc+0.0125q2c)=(0.0125q2c−2.25qc+101.25)0=0.0125q2c−2.25qc+101.25=2.25±√−2.252−4(0.0125)(101.25)2(0.0125)=2.25±√00.025qLc=90
Entry Deterrence Example: Constant Returns to Scale
qLc=90
This sets the market price to
p=5−0.05(90)p=0.50
i.e. marginal cost!
- This is the Bertrand/perfectly competitive outcome, but with one firm!
- p=MC=0.50, πc=πp=0
Entry Deterrence Example: Constant Returns to Scale
At qLc=90, Pepsi's best response is to produce 0 (i.e. stay out of the market)
But Coke earns πc=0!
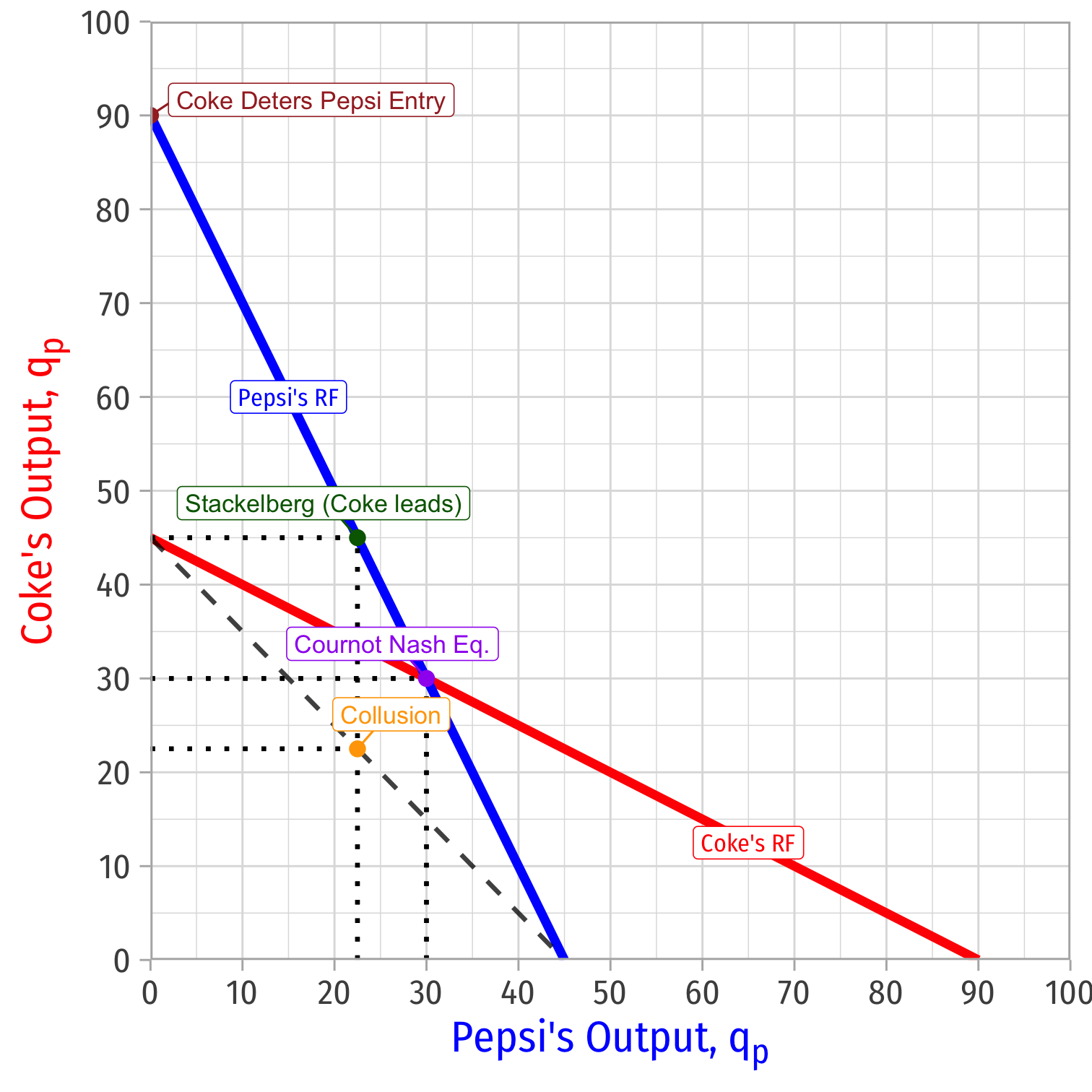
Entry Deterrence Example: Constant Returns to Scale
With constant returns to scale (and identical technology), Leader cannot credibly deter entry by Follower (and itself earn profits)!
- No penalty for small scale production (Follower could produce even a tiny amount and earn positive profits!)
Limit price is MC and profits for both firms are zero, i.e. the Bertrand or Perfectly Competitive outcome!
It is rational for Leader to optimally accommodate (produce Stackelberg amount!) as opposed to deter entry

Entry Deterrence Example: Economies of Scale
- With economies of scale and fixed costs, consider if both firms have the same technology: C(qi)=cqi+f
- c is variable (marginal) costs
f represents entry costs; as ↑f, the greater the economies of scale
Follower considering entry must weigh its post-entry profits π2=(p−c)q2 vs. the cost of entry f
Example: If c=0.50 (again), and f is 20, find the limit output for Firm 1 (Coke)
πp=(p−c)qpπp=(a−bqc−bqp−c)qp−fπp=(5−0.05qc−0.05qp−0.50)qp−20πp=(5−0.05qc−0.05[45−0.5qc]−0.50)[45−0.5qc]−20=(5−0.05qc−2.25+0.025qc−0.5)[45−0.5qc]−20=(2.25−0.025qc)[45−0.5qc]−20=(101.25−1.125qc−1.125qc+0.0125q2c)−20=(0.0125q2c−2.25qc+101.25)−200=0.0125q2c−2.25qc+81.25=2.25±√−2.252−4(0.0125)(81.25)2(0.0125)=2.25±√5.0625−4.06250.025=2.25±10.025qLc=50
Entry Deterrence Example: Economies of Scale
With Coke producing 50, Pepsi's best response would be to produce 20
This would set p=5−0.05(70)=1.50
Coke's gross profit would be πc=(1.50−0.50)50=50.
- Less the $20 fixed cost, a total profit of $30
Pepsi's gross profit would be πp=(1.50−0.50)20=20
- Less the $20 fixed cost, a total profit of $0
Fixed cost moves Pepsi up and to the left on its best response curve
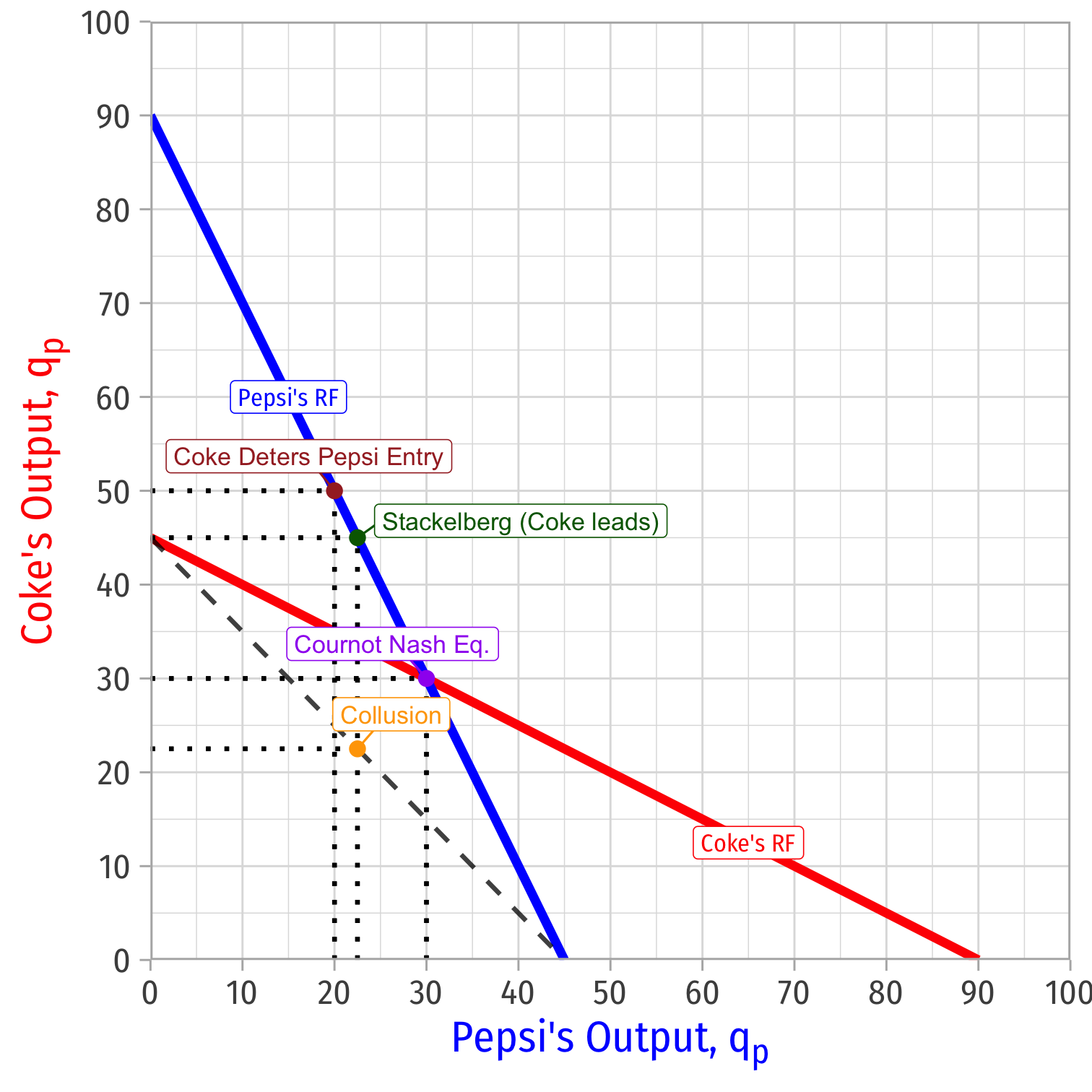
Entry Deterrence Example: Economies of Scale
Since Pepsi stays out of the market at Coke's limit output of 50, Coke's profits with deterrence are:
This would set the limit price of
p=5−0.05(50)p=2.50
- Coke’s total profits (including fixed costs):
πc=(2.50−0.50)50−20=80.

Entry Deterrence Example: Economies of Scale
- In general, qL1=(a−c−√4bf)b, as ↑f, ↓qL1
| f | Coke's Stackelberg Profits | Coke's Entry Deterrence Profits |
|---|---|---|
| 0.25 | 50.38 | 18.87 |
| 0.50 | 50.13 | 25.96 |
| 3.00 | 47.63 | 54.71 |
| 5.00 | 45.63 | 65.00 |
| 10.00 | 40.63 | 77.28 |
| 20.00 | 30.63 | 80.00 |
| 50.00 | 0.63 | 34.60 |
| 64.00 | -13.37 | 1.99 |
Coke prefers entry deterrence over accommodation when f > 3
But as f gets too large, even a Coke monopoly becomes less profitable
Dixit Model
Textbook provides a good example of a more complex model of entry deterrence (based on Dixit 1980), p.488-507, a two-stage game:
- Incumbent (firm 1) can sink (nonrecoverable) investment in a capacity size k1 at cost r
- Entrant observes k1, then decides whether to enter at entry cost f, and then both compete Cournot-style
Essentially, investing in excess capacity creates an opportunity to deter potential entrants through a price war
Alternatively, investments in capacity may lower incumbent’s MC below entrant’s
Investments in capacity are sunk costs

Dixit Model
Essentially, investment in capacity is a sunk cost, used to potentially deter entry
- Firm 1 invests in capacity to ensure it can produce the limit output to deter Firm 2 from entry
With significant economies of scale (fixed costs), need not invest in excess capacity since monopoly output may be at least as large as the limit output to deter Firm 2
With limited economies of scale, firm 1 would need to strategically over-invest in capacity (beyond monopoly level) to commit to deterring firm 2

Takeaways about Deterrence
Suggests necessary requirements for profitable strategic entry deterrence (with identical products and costs):
- ability of incumbents to reduce their marginal costs postentry via sunk expenditures
- economies of scale
If the incumbent’s capacity investments are not sunk, then Firm 1 can’t commit to producing more than Cournot (no credible threat)
Without economies of scale, there is no profitable entry deterrence (as we saw above)

Deterrence and Credibility
So we saw how economies of scale can change the game, why?
Return to the constant returns to scale case, and let’s buckle up for some more game theory

A Simple Entry Game
Entry Game: Extensive Form
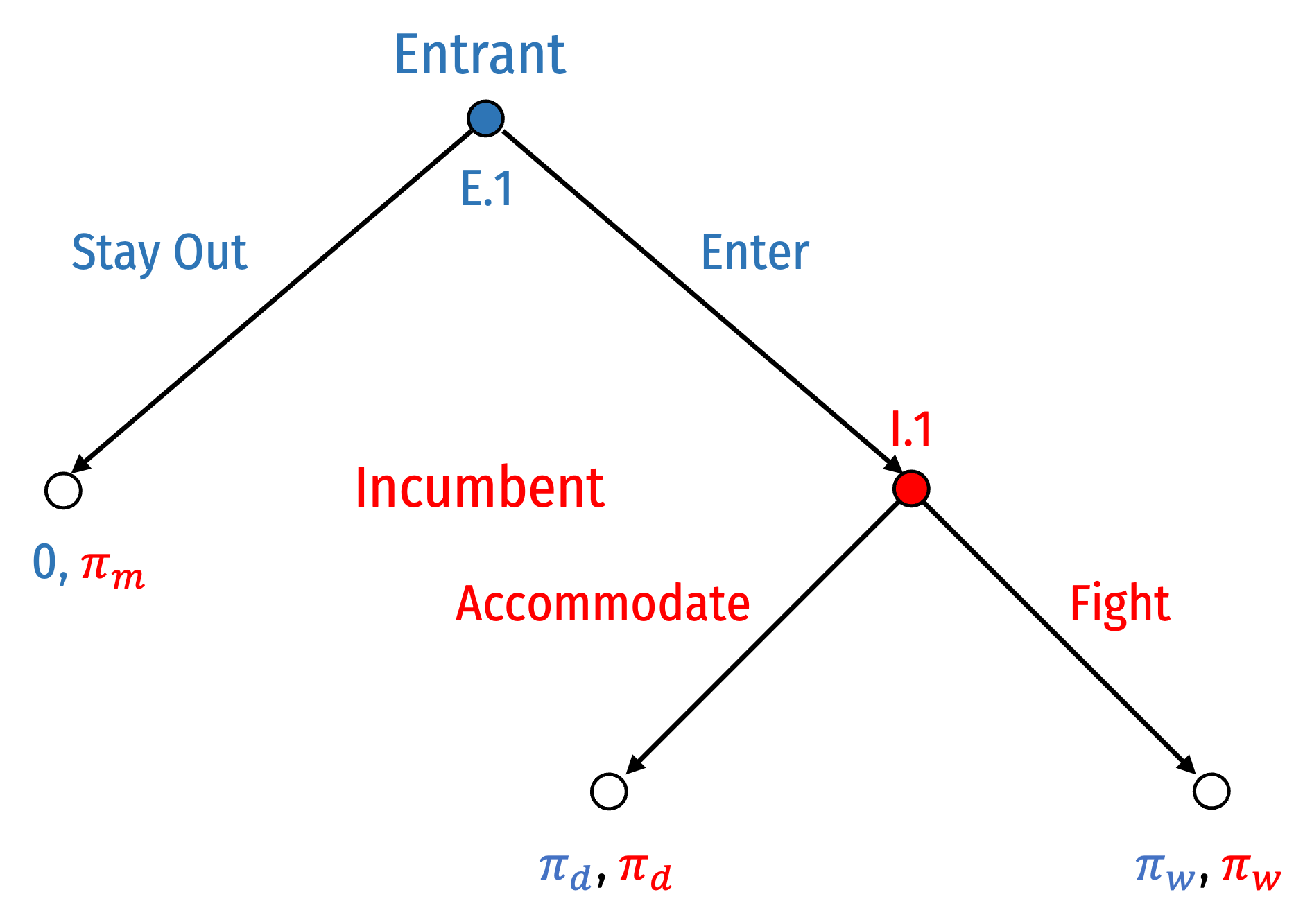
Consider a stylized Entry Game†, between an Incumbent (Coke) and a (potential) Entrant (Pepsi)
A sequential game: Entrant moves first, Incumbent moves second
Payoffs:
- πm: monopoly profits
- πd: duopoly (Cournot) profits
- πw: profits during a price war
† Famously based on Dixit 1982
Dixit, Avinash, 1982, “Recent Developments in Oligopoly Theory,” American Economic Review 72(2): 12-17
Entry Game: Extensive Form
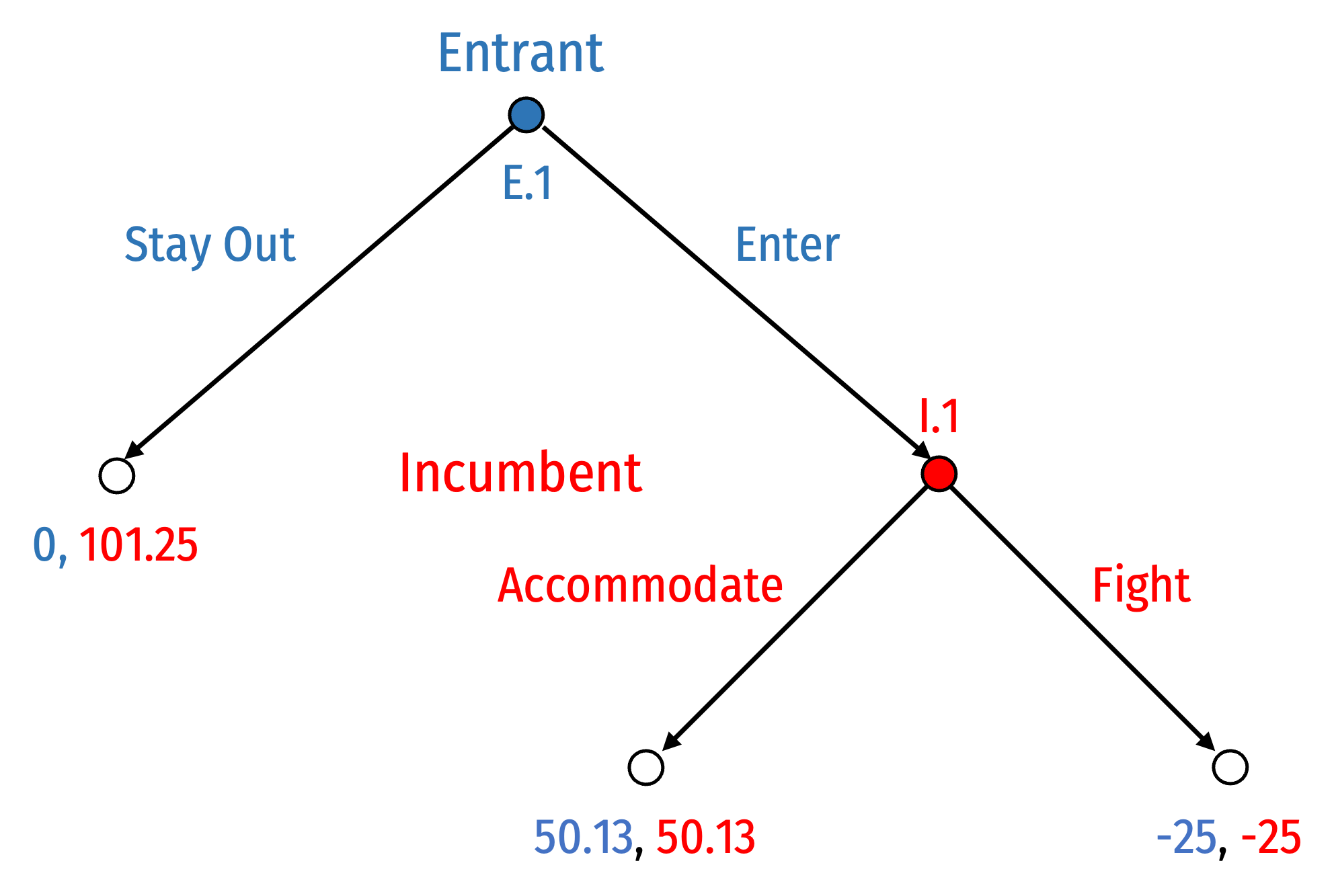
Let’s use the monopoly and Cournot payoffs from lesson 2.2
Suppose in a price war, each firm loses $25
Pure Strategies

Entrant has 2 pure strategies:
- Stay Out at E.1
- Enter at E.1
Incumbent has 2 pure strategies:
- Accommodate at I.1
- Fight at I.1
Note Incumbent's strategy only comes into play if Entrant plays Enter and the game reaches node I.1
Solving via Backward Induction

Backwards induction: to determine the outcome of the game, start with the last-mover (i.e. decision nodes just before terminal nodes)
What is that mover's best choice to maximize their payoff?
i.e. we start at I.1 where Incumbent can:
- Accommodate to earn 50.13
- Fight to earn -25
Solving via Backward Induction
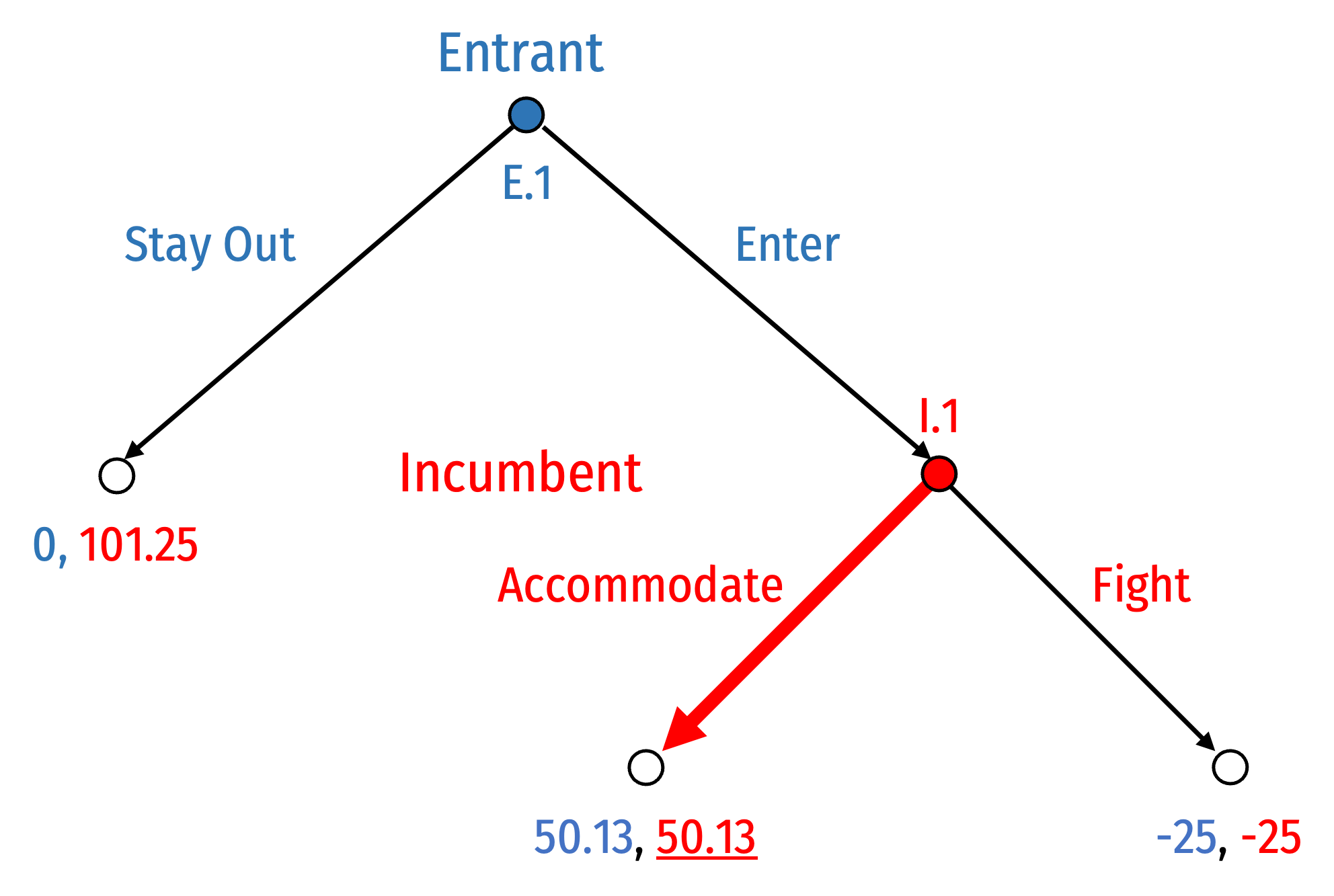
Incumbent will Accommodate if game reaches I.1
Given this, what will Entrant do at E.1?
- Stay Out to earn 0
- Enter, knowing Incumbent will Accommodate, and so will earn 50.13
Solving via Backward Induction
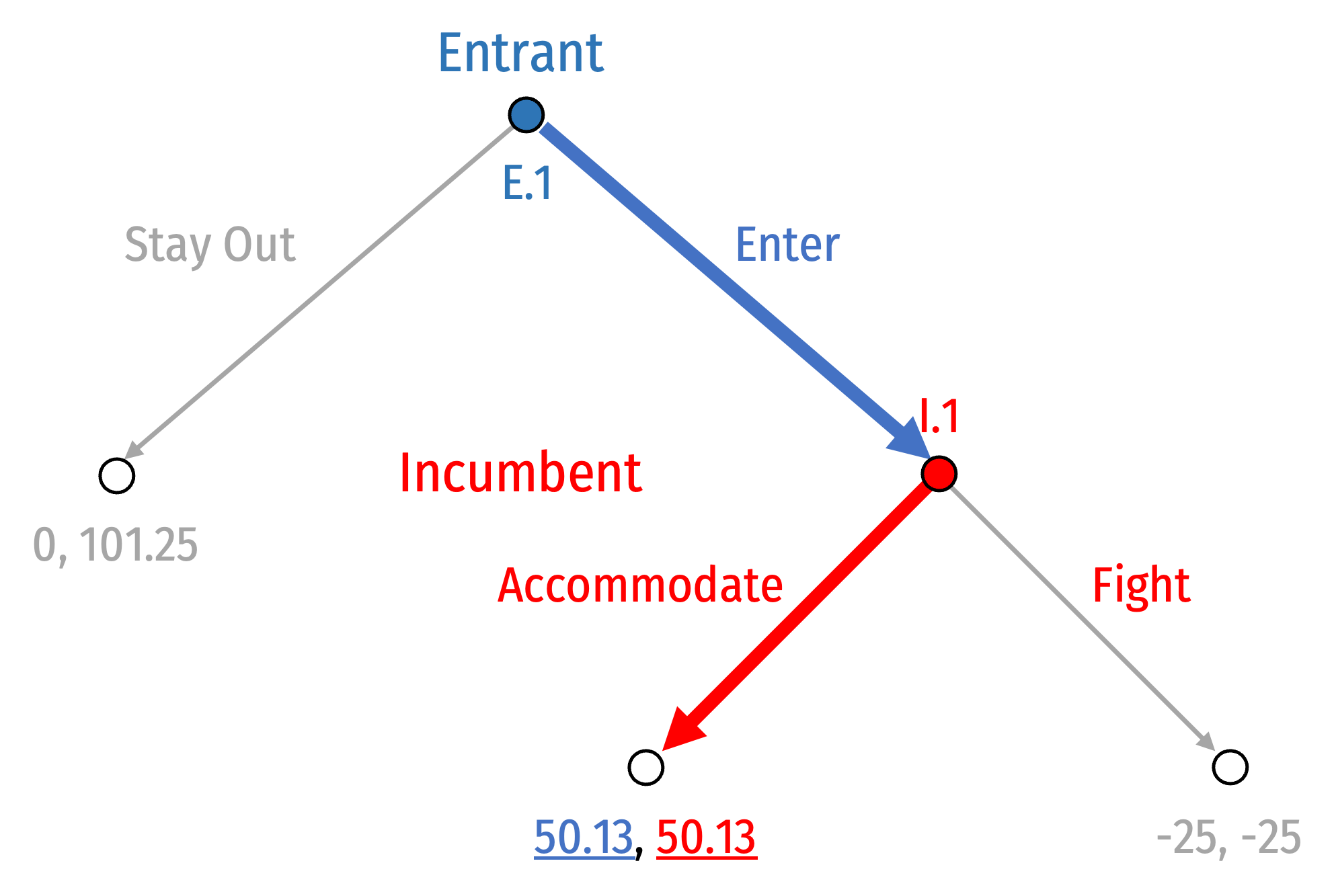
Entrant will Enter
Continue until we've reached the initial node (beginning)
We have the Nash equilibrium:
(Enter, Accommodate)
Sequential Games: Normal vs. Extensive Form

Any game in extensive form can also be depicted in “normal” or “strategic” form (a payoff matrix)
Note, if Entrant plays Stay Out, doesn't matter what Incumbent plays, payoffs are the same
Sequential Games: Normal vs. Extensive Form

- Solve this for Nash Equilibrium...
Sequential Games: Normal vs. Extensive Form

Solve this for Nash Equilibrium...
Two Nash Equilibria:
- (Enter, Accommodate)
- (Stay Out, Fight)
But remember, we ignored the sequential nature of this game in normal form
- Which Nash equilibrium is “sequentially rational?”
New solution concept: “subgame perfect Nash equilibrium” (SPNE)
Subgame Perfection
Subgames

Subgame: any portion of a full game initiated at one node and continuing until all terminal nodes
- i.e. any decision node starts a subgame containing all the “branches” of that decision node
Every full game is itself a subgame
How many subgames does this game have?
Subgames
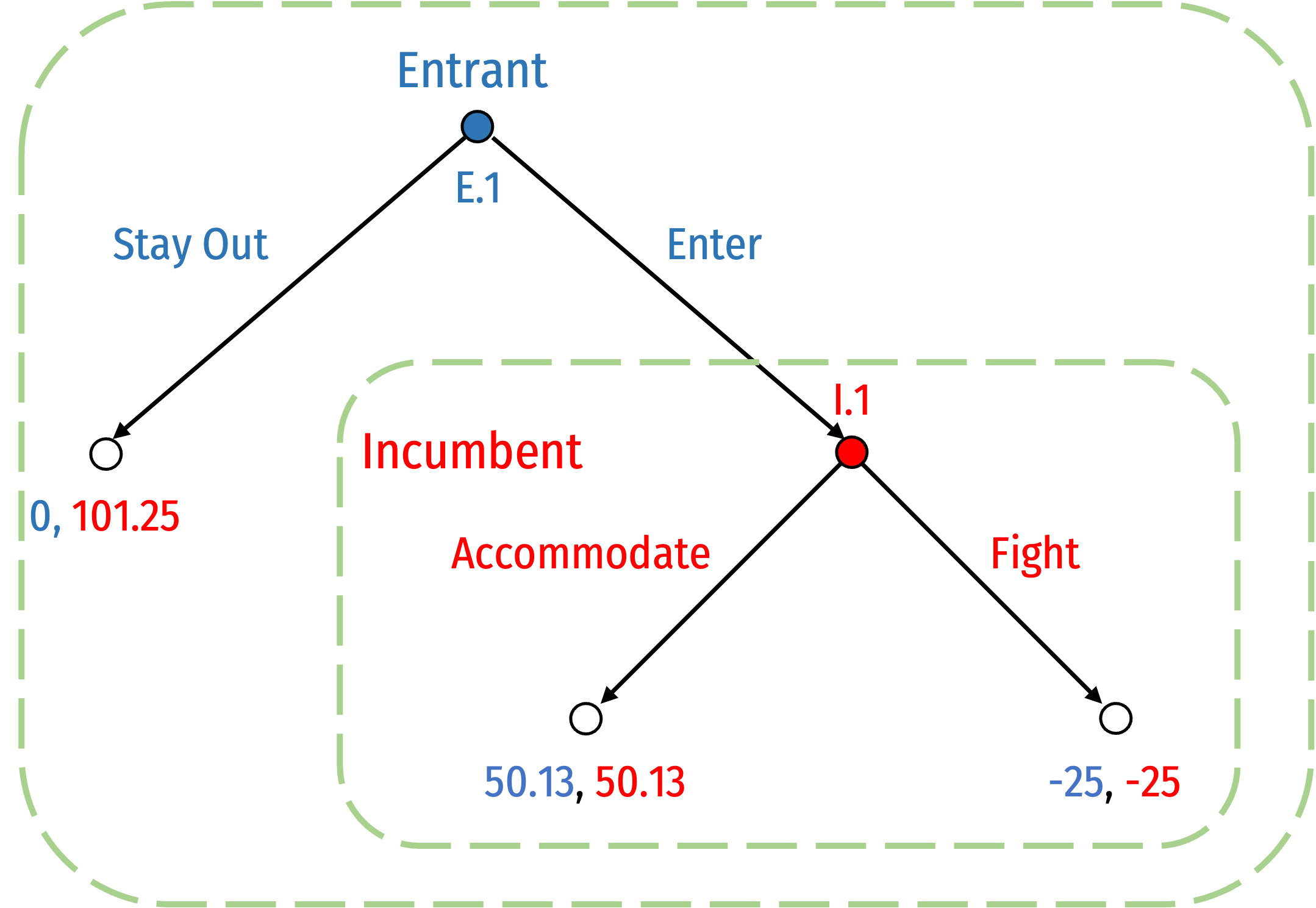
- Subgame initiated at decision node E.1 (i.e. the full game)
- Subgame initiated at decision node I.1
Subgame Perfect Nash Equilibrium

Consider each subgame as a game itself and ignore the “history” of play that got a to that subgame
- What is optimal to play in that subgame?
Consider a set of strategies that is optimal for all players in every subgame it reaches
- No player would want to change their strategy given the other’s
That’s “subgame perfect Nash equilibrium”
Subgame Perfect Nash Equilibrium


- Recall our two Nash Equilibria from normal form:
- (Enter, Accommodate)
- (Stay Out, Fight)
Subgame Perfect Nash Equilibrium


- Recall our two Nash Equilibria from normal form:
- (Enter, Accommodate)
- (Stay Out, Fight)
Consider the second set of strategies, where Incumbent chooses to Fight at node I.1
What if for some reason, Incumbent is playing this strategy, and Entrant unexpectedly plays Enter??
Subgame Perfect Nash Equilibrium


It’s not rational for Incumbent to play Fight if the game reaches I.1!
- Would want to switch to Accommodate!
Incumbent playing Fight at I.1 is not a Nash Equilibrium in this subgame!
Thus, Nash Equilibrium (Stay Out, Fight) is not sequentially rational
- (Though it is still a Nash equilibrium!)
Subgame Perfect Nash Equilibrium


Only (Enter, Accommodate) is a Subgame Perfect Nash Equilibrium (SPNE)
These strategy profiles for each player constitute a Nash equilibrium in every possible subgame!
Simple trick: backwards induction always yields the unique SPNE!
SPNE and Credibility


Suppose before the game started, Incumbent announced to Entrant, “if you Enter, I will Fight!”
This threat is not credible because playing Fight in response to Enter is not rational!
The strategy is not Subgame Perfect!
Strategic Moves & Commitment
Strategic vs. Tactical Choices in Game Theory
Strategic move: must occur prior to tactical choices, and must include commitment (i.e. irreversibility)
- Early stage of game; or “pre-game”
Tactical move: occur after strategic choices
- Choices made “in-game,” or later stages of game
- Depend on the strategic choices made earlier

Strategic Choices and Time-Horizons
Consider the difference in time-horizons across certain types of producer decisions
Shorter-run decisions depend upon the longer-run decisions!
Very long run
- Research and development
Long run
- Capacity (choice of capital, K)
- Product characteristics
- Vertical integration
- Marketing
Short run
- Quantity of output
- Price

SPNE and Credibility

Suppose I were to announce that if you were late once to class, I gave you an F
If you believe my threat, you would arrive on time, and I never have to carry out my threat
Sounds like a Nash equilibrium...but not subgame perfect!
If you call my bluff and come late, I don't actually want to carry out my policy!
Incentive Compatibility


“Talk is cheap” in game theory
With perfect information, strategic promises or threats will not change equilibrium if they are not credible
- Must be “sequentially rational” or SPNE strategy
Strategy must be incentive-compatible, if game reaches the relevant node, it must be in your interest to carry out your promise or threat!
Strategic Moves AKA “Game Changers”
So far, assumed rules of the game are fixed
In many strategic situations, players have incentives to try to affect the rules of the game for their own benefit
- Order, available strategies, payoffs, repetition
A strategic move (“game changer”) is an action taken outside the rules an existing game by transforming it into a two-stage game
- A strategic move is made in stage I (“pre-game” move)
- A modified version of the original game is played in stage II

Types of Strategic Moves
Threats: if other players don’t choose your preferred move, you will play in a manner that will be bad for them (in second stage)
- Conditional response to other players’ actions
Promises: if other players choose your preferred move, you will play in a manner that will be good for them (in second stage)
- Conditional response to other players’ actions
Commitments: irreversibly limit your choice of action, unconditional on other players’ actions

Strategic Moves and Credibility
Key: threats and promises are often costly if you must carry them out against your own interest!
If a threat works and elicits the desired behavior in others, no need to carry it out
If a promise elicits the desired behavior in others, cost of performing the promise

Commitments
A commitment is an action taken unconditional on other players' actions that limits your own actions
Only a visible and irreversible commitment makes a strategic threat or promise credible
- forces you to follow through with your threat/promise, even, and especially, if you don't actually want to
Can change outcomes of second-stage games; changes other players' expectations of the consequences of their own actions

Credible Commitment

Odysseus and the Sirens by John William Waterhouse, Scene from Homer’s Odyssey
Another Motivating Example: Why Professors Are Mean
Most professors have a lateness policy where late homework is either not accepted, or points are lost
Not (necessarily) because professors are mean!
Suppose a student hands in homework late and has a plausible excuse
Most professors actually are generous and accommodating, will make an exception
But if students know this, all students will try plausible excuses and everything becomes late

Another Motivating Example: Why Professors Are Mean
Professor can commit to a bright-line policy from the beginning (i.e. in syllabus)
Removes professor's discretion in individual cases
The policy may be "mean", but leads to a better Nash equilibrium by tying professor's hands
Salespeople have same limitations from “their manager” or “the man upstairs” preventing better deals

What Doesn't Kill You Makes You Stronger
Committing to something is costly in the short-run, but often makes the commit-er better off in the long run
Often need some kind of commitment device to artificially constrain your ability to react

What Doesn't Kill You Makes You Stronger

Thomas Schelling
1921—2016
Economics Nobel 2005
“‘Bargaining power’ suggests that the advantage goes to the powerful, the strong, or the skillful. It does, of course, if those qualities are defined to mean only that negotiations are won by those who win...The sophisticated negotiator may find it difficult to seem as obstinate as a truly obstinate man,” (p.22).
“Bargaining power [is] the power to bind oneself,” (p.22).
What Doesn't Kill You Makes You Stronger

Thomas Schelling
1921—2016
Economics Nobel 2005
“How can one commit himself in advance to an act that he would in fact prefer not to carry out in the event, in order that his commitment may deter the other party? ... In bargaining, the commitment is a device to leave the last clear chance to decide the outcome with the other party, in a manner that he fully appreciates; it is to relinquish further initative, having rigged the incentives so that the other party must choose in one's favor. If one driver speeds up so that he cannot stop, and the other realizes it, the latter has to yield...This doctrine helps to understand some of those cases in which bargaining 'strength' inheres in what is weakness by other standards.,” (p.22).
Why Are the Following So Difficult?
New Years Resolutions
Waking up early
Dieting
Going to the gym

Time-Inconsistency Problem
- Time inconsistency problem: Future you will have different preferences at the moment of truth than Present you has now


Time-Inconsistency and Commitment Devices
With a commitment device you can bind yourself in the future to obey your present wishes
Limiting your future choices keeps your preferences consistent over time
Examples:
- Deadlines
- Rely on other people
- Stake your reputation on it
- Impose a high cost on yourself for failure
- Hire an agent who is compensated based on your success

Entry Game with Commitment
Entry Game with Credible Commitment
Return to our Coke (incumbent) and Pepsi (entrant) entry game
Suppose that before Entrant can decide to Enter or Stay Out, Incumbent can choose to signal it will respond to any entry Aggressively
- invest in excess capacity; i.e. a “war chest” of superfluous infrastructure that costs -f
But with this, in response to Entrant playing Enter, Incumbent is in a better position to survive Fight a price war that forces Entrant out of the market

Entry Game with Credible Commitment
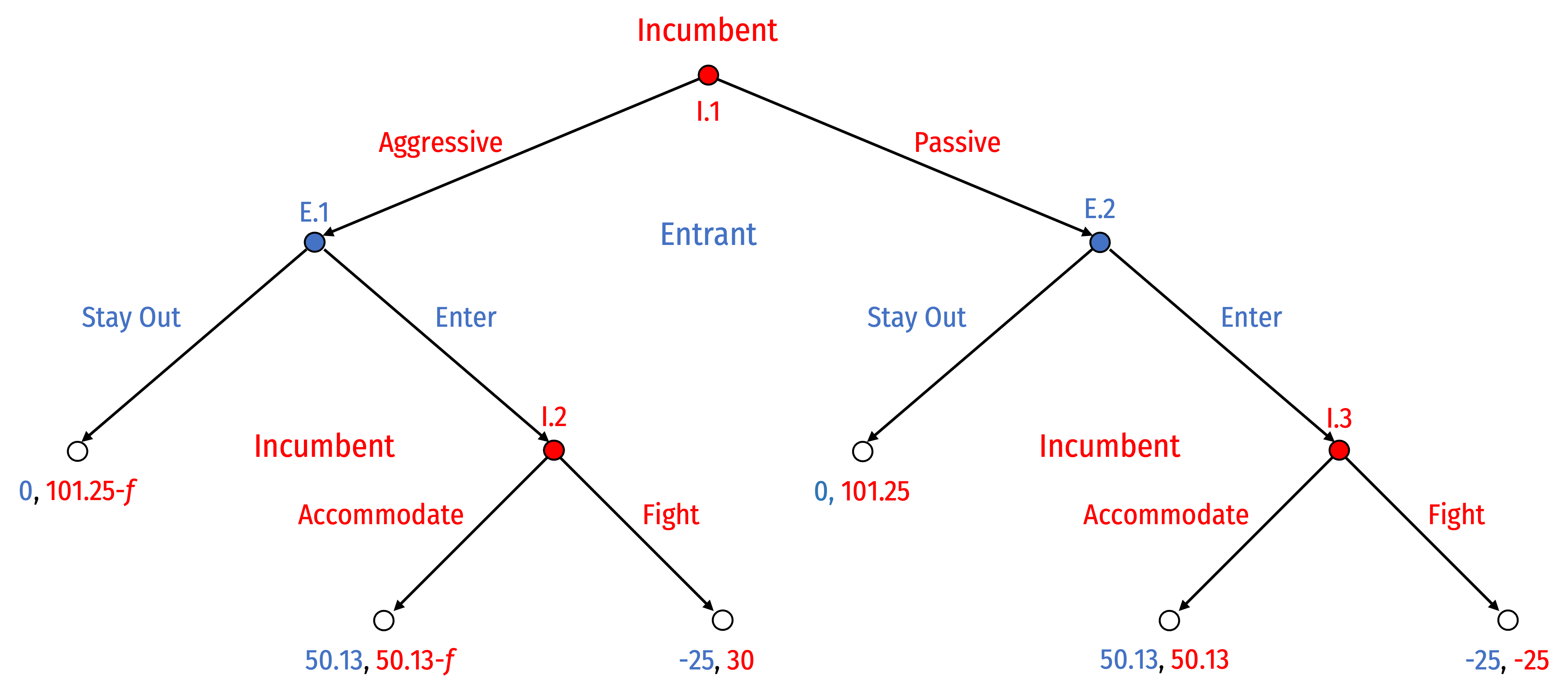
Game changes, Incumbent goes first at (new) I.1, deciding whether to signal it will be Aggressive or Passive
- Game is the same as before from E.2 onwards
This is a more complicated game, let's apply what we've learned...

Entry Game with Credible Commitment

- What are the subgames?
Entry Game with Credible Commitment
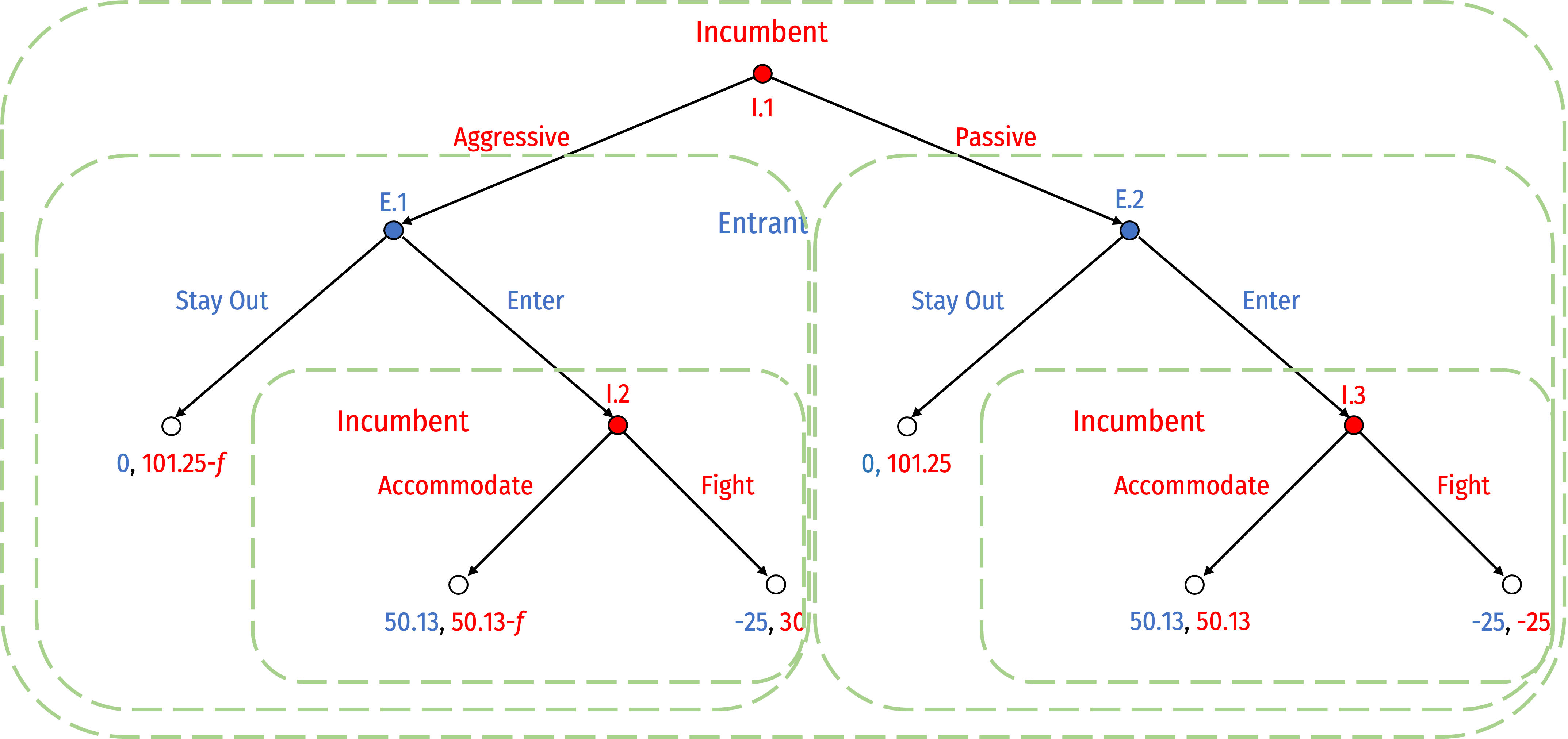
- What are the subgames?
- Subgame initiated by node I.1 (game itself)
- Subgame initiated by node E.1
- Subgame initiated by node E.2
- Subgame initiated by node I.2
- Subgame initiated by node I.3
Entry Game with Credible Commitment

- What are the strategies available to each player?
Entry Game with Credible Commitment

What are the strategies available to each player?
Entrant, choosing at nodes (E.1, E.2)
- (Stay Out, Stay Out)
- (Stay Out, Enter)
- (Enter, Stay Out)
- (Enter, Enter)
Entry Game with Credible Commitment

What are the strategies available to each player?
Incumbent, choosing between two options each at nodes (I.1, I.2, I.3), has 23=8 possible strategies:
- (Aggressive, Accommodate, Accommodate)
- (Aggressive, Accommodate, Fight)
- (Aggressive, Fight, Accommodate)
- (Aggressive, Fight, Fight)
- (Passive, Accommodate, Accommodate)
- (Passive, Accommodate, Fight)
- (Passive, Fight, Accommodate)
- (Passive, Fight, Fight)
Entry Game with Credible Commitment

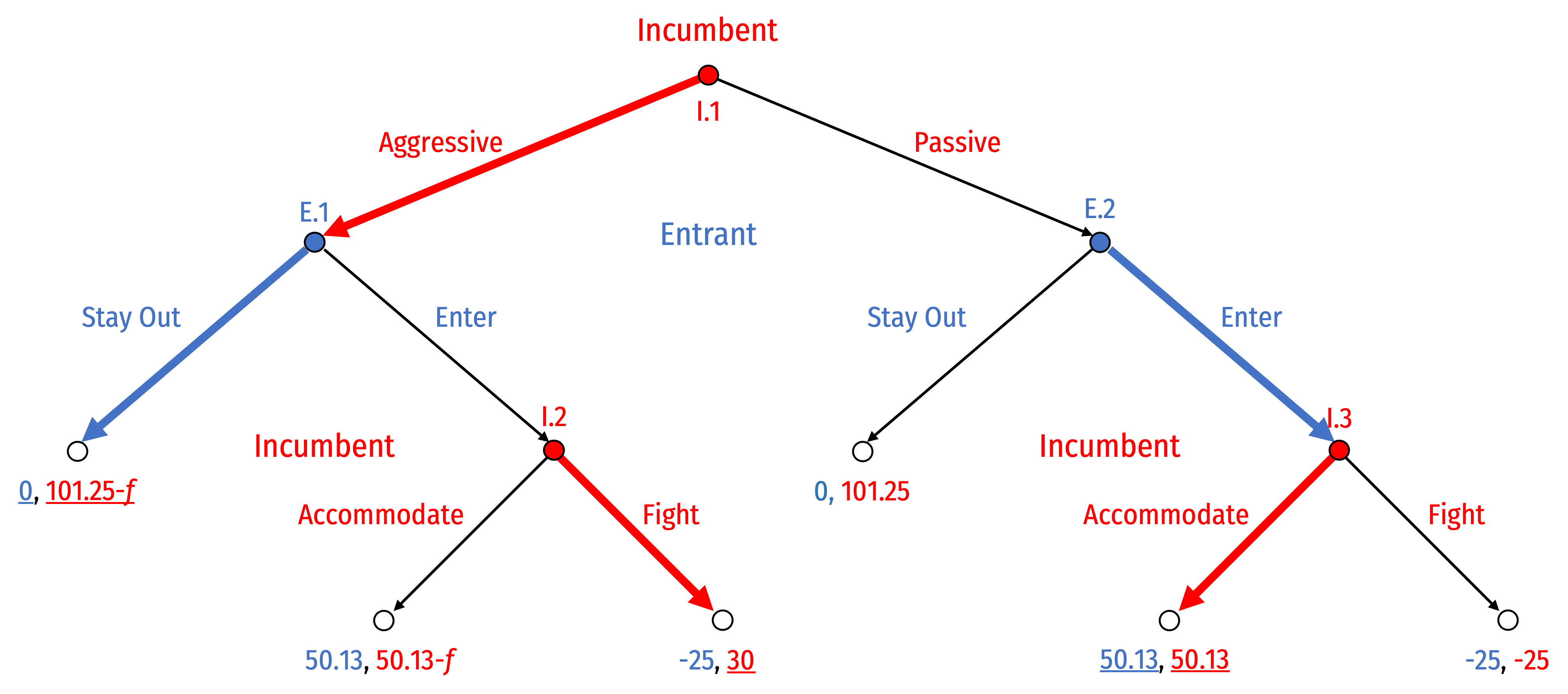
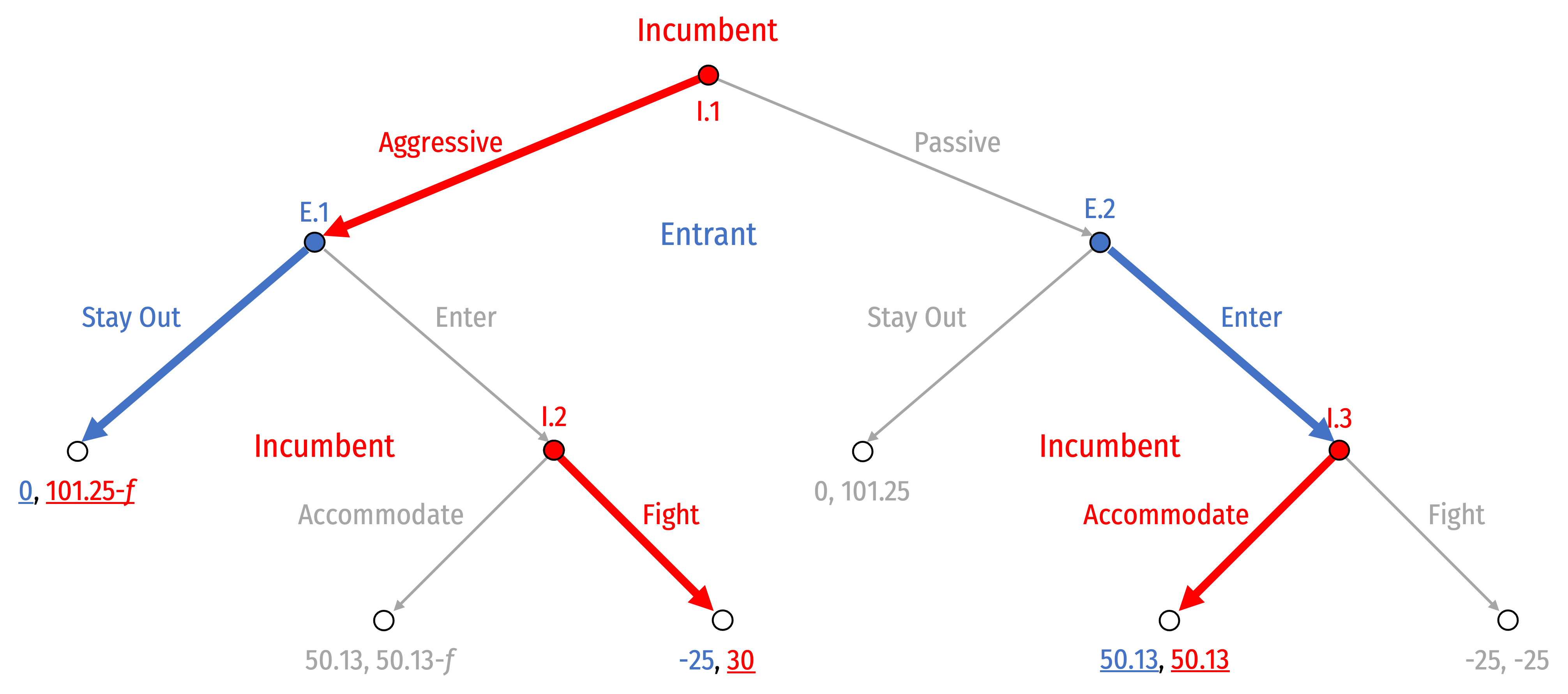
We can use backwards induction to find the outcome of the game
Let’s assume f > 20.13 (to make Aggressive-Fight worthwhile)
Start with best response of Incumbent at I.2 and I.3...then best response of Entrant at E.1 and E.2...then Incumbent at I.1


Entry Game with Credible Commitment

- With f > 20.13, Subgame Perfect Nash Equilibrium (SPNE):
(Aggressive, Fight, Accommodate), (Stay Out, Enter)
- The equilibrium path of play is Aggressive, then Stay Out
Entry Game with Credible Commitment

(Aggressive, Fight, Accommodate), (Stay Out, Enter)
SPNE: this set of strategies induces a Nash equilibrium in every subgame
- Each player optimally responding to every contigency
With commitment, it is credible for Incumbent to threaten to Fight if Entrant decides to Enter!
Entry Game with Credible Commitment: Normal Form
(Aggressive, Fight, Accommodate), (Stay Out, Enter)
- Note we could look at the set of strategies in normal form
Entry Game with Credible Commitment: Normal Form

(Aggressive, Fight, Accommodate), (Stay Out, Enter)
- Note we could look at the set of strategies in normal form
Entry Game with Credible Commitment: Normal Form

(Aggressive, Fight, Accommodate), (Stay Out, Enter)
- Note we could look at the set of strategies in normal form
Entry Game with Credible Commitment: Normal Form

(Aggressive, Fight, Accommodate), (Stay Out, Enter)
- Note we could look at the set of strategies in normal form
- But only the one mentioned above is subgame perfect!

Market Contestability
Contestable Markets
Markets are perfectly contestable if:
- Entry and exit are free
- Firms have similar technologies (i.e. similar cost structure)
- May have economies of scale (fixed costs), but there are no sunk costs
Generalizes “perfect competition” model in more realistic way, also game-theoretic

Contestable Markets

William Baumol
(1922--2017)
“This means that...an incumbent, even if he can threaten retaliation after entry, dare not offer profit-making opportunities to potential entrants because an entering firm can hit and run, gathering in the available profits and departing when the going gets rough.”
Baumol, William, J, 1982, "Contestable Markets: An Uprising in the Theory of Industry Structure," American Economic Review, 72(1): 1-15
Contestable Markets
“Hit-and-run” competition forces the incumbent to the limit price
Incumbent is constrained by the threat of entry or potential competition, rather than actual competition
Can get perfectly competitive outcome with a single firm!


An Entry Game
- Model the market as an entry game, with two players:
Incumbent which sets its price pI
Entrant decides to stay out or enter the market, setting its price pE
- Bertrand (price) competition between 2 firms with similar products ⟹ consumers buy only from firm with lower price


Contestable Markets II
Suppose both firms have identical costs: C(q)=cqMC(q)=c
If Incumbent sets pI>c
- Entrant would enter and set pE=pI−ϵ†

† For arbitrary ϵ>0, think ϵ= “one penny”
Contestable Markets II
Suppose both firms have identical costs: C(q)=cqMC(q)=c
If Incumbent sets pI>c
- Entrant would enter and set pE=pI−ϵ†
- Incumbent foresees this possibility, and wants to lower its price pI<pE
- This potential undercutting would continue logically until...

† For arbitrary ϵ>0, think ϵ= “one penny”
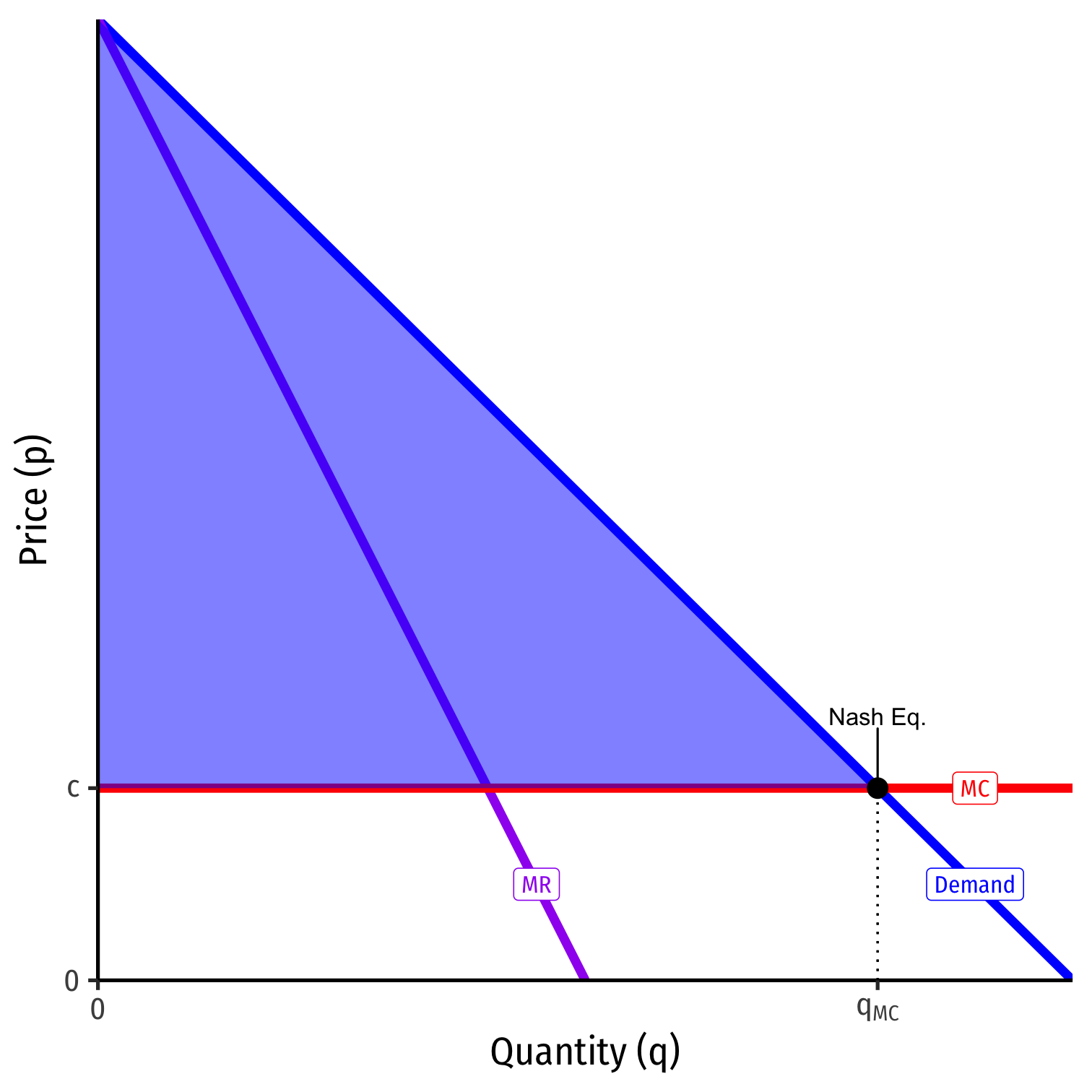
Contestable Markets II
Nash Equilibrium: (pI=c, Stay Out )
A market with a single firm, but the competitive outcome!
- p∗=MC, π=0
- competitive q∗
- max Consumer Surplus, no DWL
Contestable Markets II
- What if the Entrant has higher costs than the Incumbent: cE>cI?
Contestable Markets II
What if the Entrant has higher costs than the Incumbent: cE>cI?
Nash equilibrium: (pI=pE−ϵ, Stay Out )
One firm again, with some inefficiency
- But not as bad as monopoly!

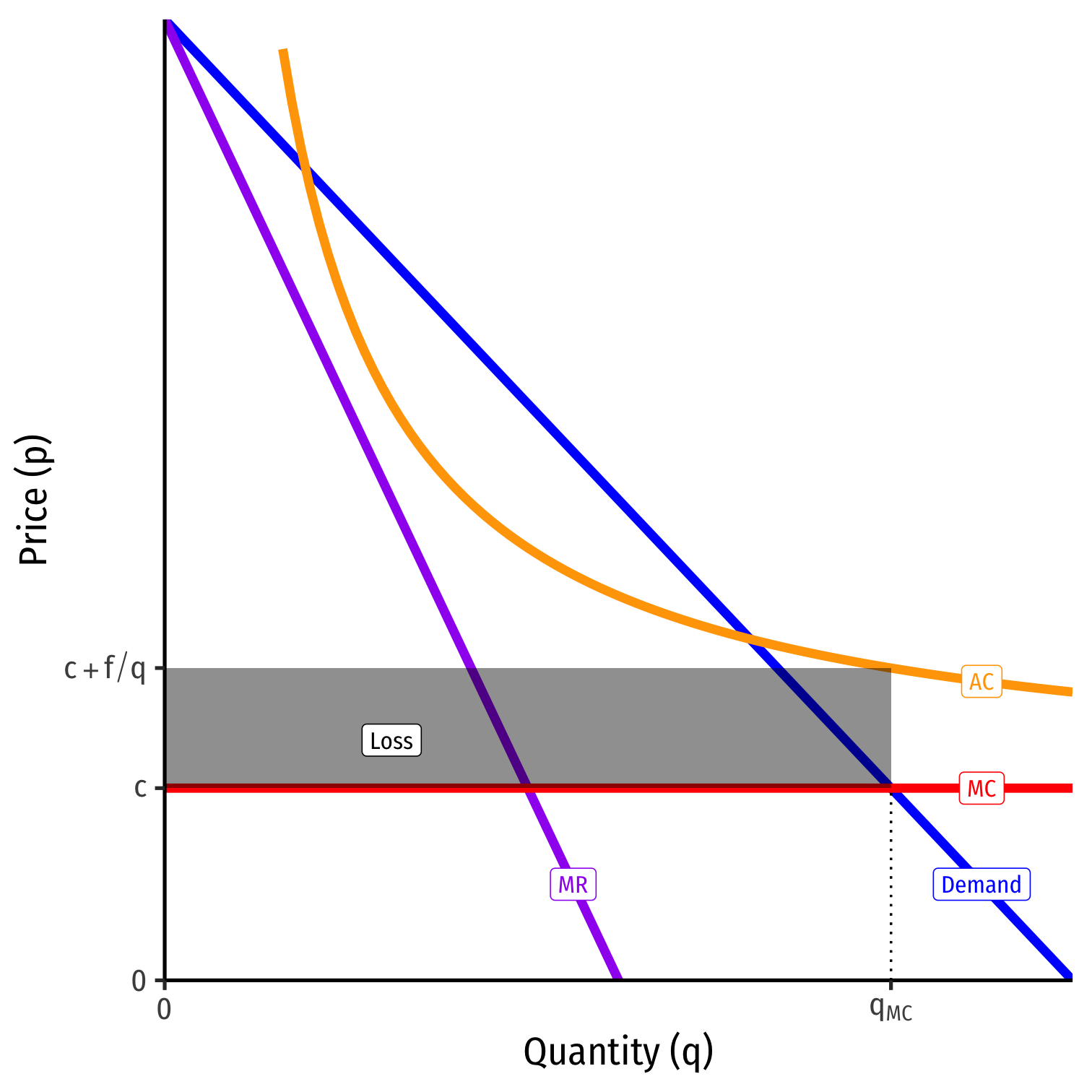
Contestable Markets III
- What if there are fixed costs, f?
C(q)=cq+fMC(q)=cAC(q)=c+fq
- With high enough f, economies of scale prevent marginal cost pricing from a being profitable Nash Equilibrium
πp=MC=−fq<0
Contestable Markets IV
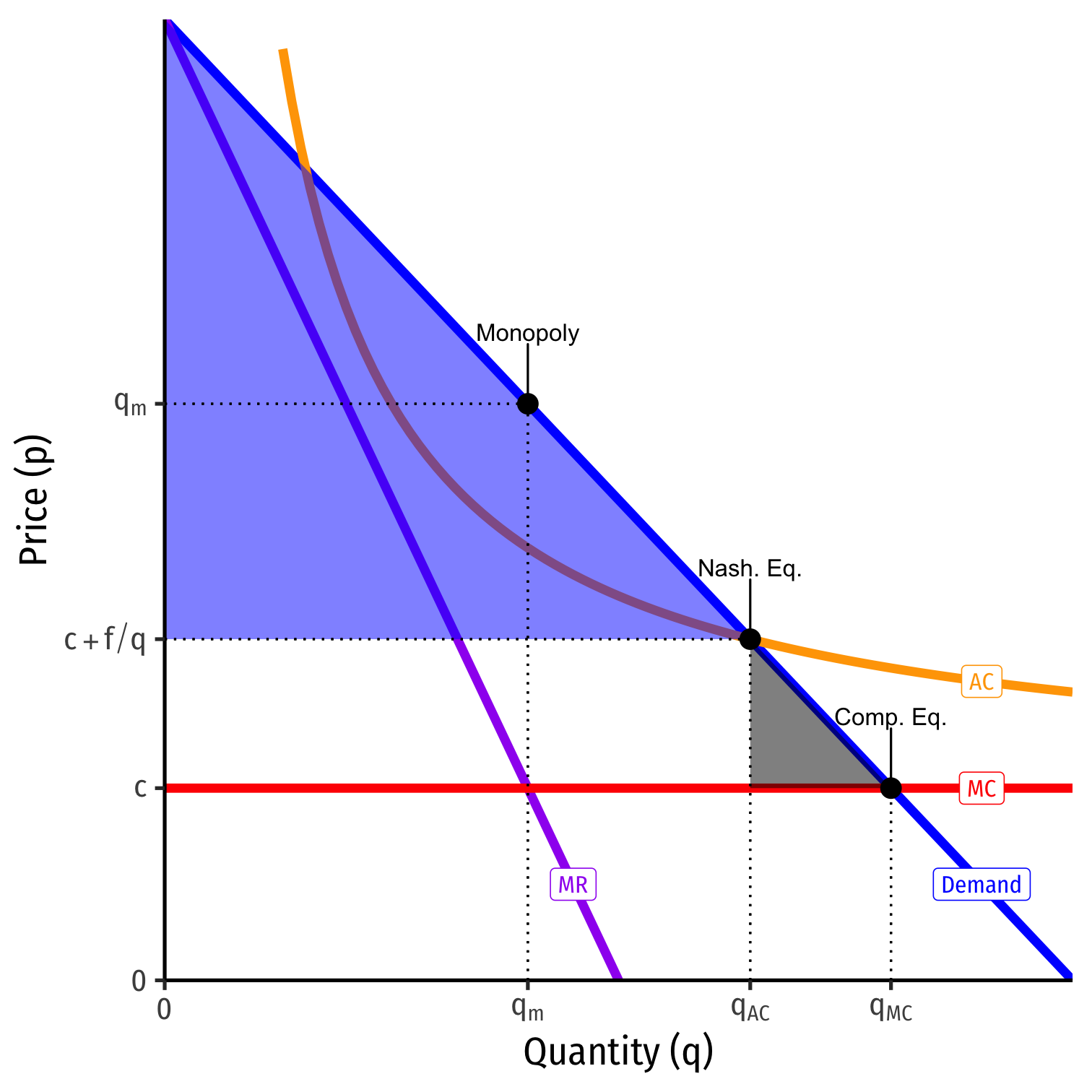
Nash equilibrium: (pI=AC, Stay Out )
Again, only a single firm with some inefficiency
- But not as bad as monopoly!
- Incumbent earns no profits!
What About Sunk Costs? I
Fixed costs ⟹ do not vary with output
If firm exits, could sell these assets (e.g. machines, real estate) to recover costs
- Thus, “hit-and-run” competition remains potentially profitable
- Maintains credible threat against incumbent acting as a monopolist

What About Sunk Costs? I
But what if assets are not sellable and costs not recoverable - i.e. sunk costs?
e.g. research and development, spending to build brand equity, advertising, worker-training for industry-specific skills, etc

What About Sunk Costs? II
These are bygones to the Incumbent, who has already committed to producing
But are new costs and risk to Entrant, lowering expected profits
In effect, sunk costs raise cE>cI, and return us back to our Scenario II
Nash equilibrium: Incumbent deters entry with pI=pE−ϵ
- Inefficient, p>AC, but again not monopoly
